Anteriormente, descrevemos o teste t para amostras pareadas, também conhecido como teste t de medidas repetidas ou teste t para amostras dependentes. Por exemplo, esse teste permite comparar os escores de um grupo de participantes antes e após uma intervenção. Neste post, mostraremos como executar o teste t para amostras pareadas no SPSS. Além disso, também mostraremos como calcular uma medida de tamanho de efeito para reportar junto ao resultado do teste t. Por fim, mostraremos como reportar os resultados da análise.

Como realizar o teste t para amostras pareadas no SPSS?
Exemplo
Suponha que pesquisadores tenham superalimentado 16 adultos não obesos durante oito semanas (Levine et al., 1999). As massas desses participantes foram mensuradas antes e após a intervenção. O objetivo era investigar se a atividade metabólica não associada a exercícios (mas associada à inquietação) se relaciona ao ganho de gordura após oito semanas.
Para este tutorial, contudo, não consideraremos o objetivo principal da pesquisa, nem descreveremos as demais medidas do estudo. Ao invés disso, nosso objetivo será realizar uma checagem de manipulação, isto é, investigar se a superalimentação conseguiu de fato produzir aumentos significativos no peso dos participantes da amostra.
A Figura 1 ilustra o banco de dados baseado nesse exemplo. Embora tabulado no SPSS, ele foi obtido junto à instalação do software JASP (Moore et al., 2009). Nesse banco de dados, cada participante contribuiu com escores em dois momentos distintos, ou seja, no pré-intervenção (weight_before_kg) e no pós-intervenção (weight_after_kg). A variável difference_kg representa o ganho de massa da medida pré- para a pós-intervenção.
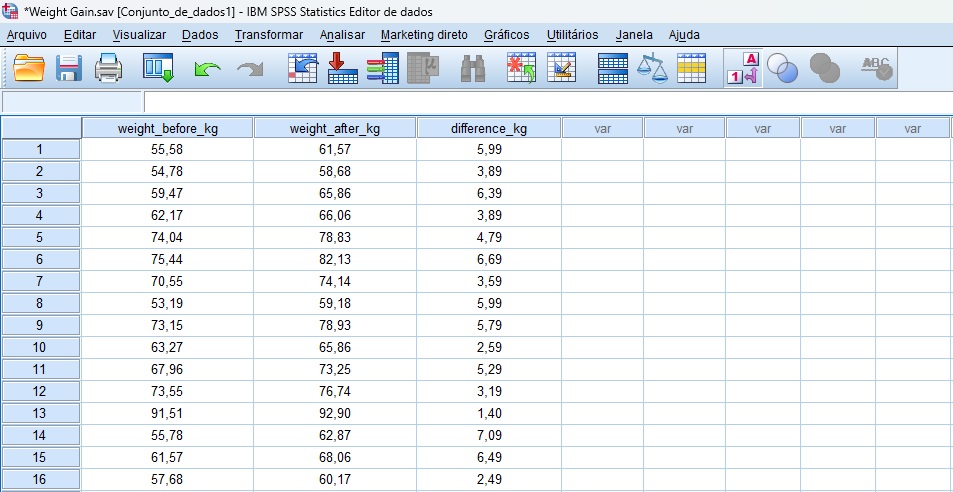
Desse modo, temos as seguintes hipóteses:
- Hipótese nula (H0): não existem diferenças nas massas médias dos participantes nas medidas pré- e pós-intervenção.
- Hipótese alternativa (H1): existem diferenças nas massas médias dos participantes nas medidas pré- e pós-intervenção.
Em seguida, o teste t para amostras pareadas testará a plausibilidade dos dados, assumindo que a hipótese nula é verdadeira. A rejeição da hipótese nula ocorrerá considerando um nível de significância de 5%, isto é, α = 0,05.
Solicitando o teste t para amostras pareadas no SPSS
Primeiramente, siga o caminho Analisar > Comparar médias > Teste-T de amostras em pares (Figura 2).
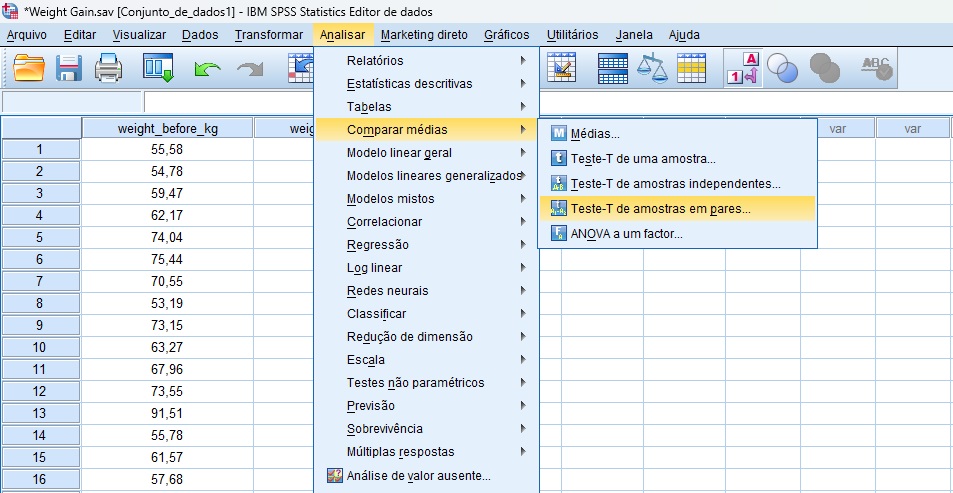
Em seguida, transfira as variáveis que você deseja comparar para o painel direito da janela. Em nosso exemplo, transferimos a variável weight_after_kg para a caixa Variável1, enquanto a variável weight_before_kg foi transferida para a caixa Variável2 (Figura 3).

A ordem de inserção das duas variáveis é irrelevante, pois o teste dará resultados similares se inserirmos as variáveis na ordem inversa, exceto que o SPSS inverterá os sinais de algumas estatísticas. Optamos por inserir weight_after_kg em Variável1, pois isso nos permite interpretar diferenças positivas como indicando ganhos de massa após a intervenção.
Para executar a análise, basta clicar em OK.
Interpretando a saída do teste t para amostras pareadas no SPSS
Primeiramente, a Figura 4 apresenta a tabela de estatísticas descritivas das amostras emparelhadas. A propósito, o termo emparelhadas é sinônimo de pareadas (do inglês, paired).
A Figura 4 indica que a massa média foi quase 5 kg maior na medida pós-intervenção (M = 70,33), quando comparada à medida pré-intervenção (M = 65,61). Se houver diferença estatisticamente significativa entre as médias nos dois momentos, isso certamente indicará que os escores são maiores após a intervenção de superalimentação.

Em seguida, a Figura 5 apresenta a tabela de correlação das medidas pareadas. A correlação de Pearson das massas dos participantes nos dois momentos é quase perfeita, r = 0,99, p < 0,001. Essa informação tipicamente é omitida de relatos, embora ela seja relevante para estimar medidas de tamanho de efeito em revisões metanalíticas.

Por fim, a Figura 6 apresenta a tabela o teste t propriamente dito. Quando consideramos o valor de p associado à estatística t, na coluna Sig. (2 extremidades), optamos por rejeitar a hipótese nula de não diferença entre as massas médias nas medidas pré- e pós-intervenção, pois o valor de p é menor que 0,05.
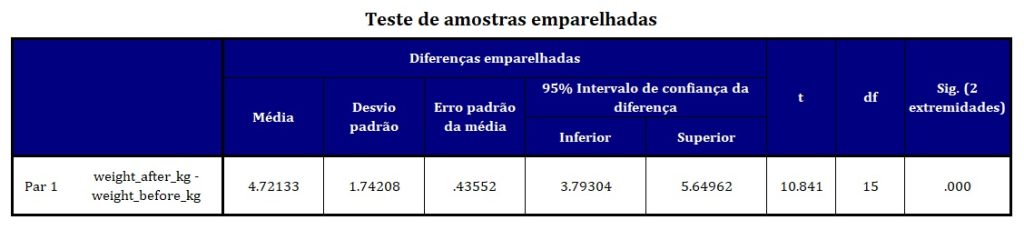
De maneira alternativa, também poderíamos interpretar a diferença entre médias e seu respectivo intervalo de confiança. Na Figura 6, coluna Média representa a diferença entre as duas médias apresentadas na Figura 4. A coluna 95% Intervalo de confiança da diferença, por sua vez, representa o intervalo de confiança de 95% ao redor da diferença média. Se os limites desse intervalo não capturarem o zero, então temos evidências de diferenças estatisticamente significativas entre pré- e pós-intervenção. É o que ocorre em nosso exemplo (note que os limites inferior e superior têm ambos valores positivos).
Calculando o tamanho de efeito para o teste t para amostras pareadas
Para avaliarmos a magnitude da diferença entre as médias, podemos computar uma estimativa de tamanho de efeito. Por exemplo, o d de Cohen é uma medida de tamanho de efeito que expressa a diferença entre as médias de dois grupos em unidades de desvio-padrão. No contexto de delineamentos com amostras pareadas, calculamos o d de Cohen por meio da fórmula a seguir:
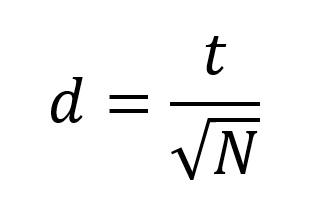
onde t se refere à estatística t apresentada na Figura 6, e N se refere ao número de pares na amostra.
Inserindo os valores de nosso exemplo na fórmula, temos:

Esse valor indica, portanto, que a diferença entre médias das medidas pré- e pós-intervenção (Mdif = 4,72) é 2,71 unidades de desvio-padrão da diferença (DPdif = 1,74; veja a Figura 6), um tamanho de efeito considerado grande.
Reportando os resultados das análises
Ao descrever os resultados, é importante apresentar a estatística t, os graus de liberdade e pelo menos uma medida de tamanho de efeito. Além disso, espera-se que você conduza o leitor às interpretações adequadas dos resultados do teste. Desse modo, apresentamos uma sugestão de relato a seguir:
A massa média de 16 adultos não obesos foi maior na medida pós-intervenção (M = 70,33, DP = 9,72) do que na medida pré-intevenção (M = 65,61, DP = 10,30). Esse aumento foi apoiado estatisticamente por meio de um teste t pareado, t(15) = 10,84, p < 0,001, d = 2,71. Concluímos, portanto, que a intervenção de superalimentação foi bem-sucedida em aumentar as massas dos participantes, apresentando um efeito grande (Cohen, 1988).
Conclusão
Neste post, você aprendeu a realizar o teste t para amostras pareadas no SPSS. Além disso, você aprendeu a calcular o d de Cohen e a reportar os resultados das análises.
Gostou desse conteúdo? Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referência
Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Academic press.
Levine, J. A., Eberhardt, N. L., & Jensen, M. D. (1999). Role of nonexercise activity thermogenesis in resistance to fat gain in humans. Science, 283(5399), 212–214. https://doi.org/10.1126/science.283.5399.212
Moore, D. S., McCabe, G. P., and Craig, B. A. (2009). Introduction to the practice of statistics (6th ed.). Freeman.
Como citar este post
Lima, M. (2021, 23 de dezembro). Como fazer o teste t para amostras pareadas no SPSS? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/tutorial-teste-t-para-amostras-pareadas-no-spss/













