Como avaliar a normalidade dos dados no SPSS? Neste post, apresentaremos um tutorial de como analisar diferentes índices e testes de normalidade nesse software.
O que é distribuição normal?
A distribuição normal é é uma distribuição de probabilidade simétrica, em forma de sino, cujos valores mais frequentes estão localizados no centro, com frequências cada vez menores à medida que nos aproximamos dos extremos da distribuição. A Figura 1 ilustra um conjunto de dados com uma distribuição aproximadamente normal.

Ela é uma distribuição importante, pois muitas técnicas estatísticas assumem algum tipo de normalidade. Por exemplo, o teste t para amostras independentes assume que os escores de cada um dos grupos são oriundos de populações normalmente distribuídas. Por outro lado, o teste t de medidas repetidas assume que os escores da diferença entre mensurações é que são normalmente distribuídos.
Desse modo, para que os testes estatísticos produzam inferências válidas, é importante checarmos se acatamos os pressupostos do teste em nossos dados. Por outro lado, quando violamos os pressupostos estatísticos, os resultados de nossos testes podem não ser confiáveis, além de nos afastarmos da taxa nominal de erro Tipo I que estabelecemos.
Além disso, se os nossos dados possuírem distribuição normal, então algumas propriedades conhecidas da distribuição se aplicarão aos nossos dados. Por exemplo, em distribuições normais, sabemos que aproximadamente 68%, 95% e 99% dos escores estão a 1, 2 e 3 desvios-padrões, respectivamente, da média (Figura 2).

Saiba mais: O que é distribuição normal?
Como avaliar a normalidade dos dados no SPSS?
Exemplos de conjuntos de dados
Para fins desse tutorial, criamos três conjuntos de dados, com 300 observações cada (Figura 3).

Observamos que apenas o primeiro conjunto (Figura 3, painel esquerdo) parece ter distribuição normal. Idealmente, portanto, nossos índices e testes estatísticos deveriam discriminar a primeira das demais distribuições.

Como solicitar os índices de normalidade dos dados no SPSS?
Primeiramente, abra seus dados e siga o caminho Analisar > Estatísticas descritivas > Explorar (Figura 4).
Em seguida, insira as variáveis que você quer testar a normalidade em Lista dependente e clique em Gráficos (Figura 5, painel esquerdo). Na nova janela que abrirá, marque a opção Gráficos de normalidade com testes (Figura 5, painel direito).

Não precisaremos mexer em Estatísticas, pois elas, por padrão, já nos apresentarão os índices de assimetria e de curtose. Basta clicar em Continuar e, em seguida, em OK. Após clicar em OK, o SPSS gerará os resultados das análises solicitadas.
Como interpretar as saídas das análises de normalidade dos dados do SPSS?
Tabela de estatísticas descritivas
A Figura 6 apresenta as estatísticas descritivas que o SPSS gerou. Contudo, visando economizar espaço, nós reconfiguramos o padrão de apresentação da tabela, que é ligeiramente diferente daquele criado pelo SPSS.

A tabela de estatísticas descritivas contém índices das variáveis, incluindo, por exemplo, medidas de tendência central e de dispersão. Uma estatística que você talvez não conheça é a média aparada de 5%. Para obter esse valor, o SPSS ordena as observações da menor para a maior, e exclui os 5% menores valores, bem como os 5% maiores. Por fim, após essa exclusão, o SPSS calcula a nova média amostral.
Diferenças substanciais entre as médias original e aparada podem indicar que valores extremos estão exercendo forte influência sobre a média original da amostra. É exatamente o que acontece na distribuição de qui-quadrado (Moriginal = 0,97, Maparada 5% = 0,74).
Em contrapartida, há pouca mudança nos valores das médias originais e aparadas, nos casos das distribuições normal e uniforme, indicando que valores extremos não influenciam substancialmente o valor da média.
Assimetria e curtose
Anteriormente, a Figura 6 apresentou valores de assimetria e curtose. Em seguida, reapresentamos esses valores na Figura 7, com uma nova configuração da tabela. Além disso, acrescentamos uma informação nova na Figura 7, indicada pelas células nas cores azul e vermelha.
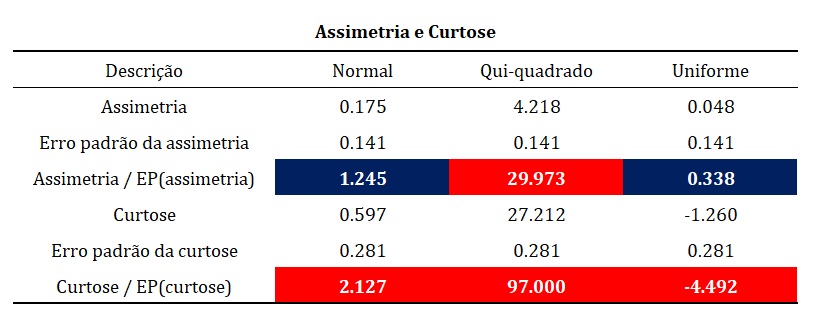
Kline (2016) sugere que valores de assimetria maiores que 3, e de curtose maiores que 10, são indicativos de problemas. No entanto, ressaltamos que outros metodólogos fazem recomendações ligeiramente distintas.
Desse modo, se considerarmos as recomendações de Kline, há desvios importantes de assimetria (S = 4,22) e de curtose (K = 29,97) na distribuição de qui-quadrado. Contudo, tomemos como exemplo a curtose da distribuição uniforme (K = –1,26). Um valor menor que 10 não indica normalidade, mas sim que a forma da distribuição não se desvia substancialmente de uma distribuição normal (na distribuição normal, S = K = 0).
Outra possibilidade de análise é realizar teste de hipóteses. Em outras palavras, podemos dividir a estatística (de assimetria ou de curtose) pelo seu respectivo erro-padrão, o que produz os valores indicados pelas células coloridas da Figura 7. Tais valores podem ser interpretados como escores z. A um nível de significância de 0,05, z > |±1,96| indicam valores significativos e, portanto, indicativos de violações de normalidade.
Nesse caso, mais uma vez, temos evidências de desvios importantes de assimetria e de curtose para a distribuição qui-quadrado. Contudo, até mesmo os dados gerados a partir de uma distribuição normal tiveram desvios de curtose (K = 2,13). Por esse motivo, Field (2017) argumenta contra o uso desses índices, pois, em amostras maiores, mesmo desvios sutis (e sem maior importância) da normalidade podem atingir significância estatística.
Saiba mais: Assimetria e curtose: um guia completo
Testes de normalidade
A Figura 8 apresenta os resultados dos testes de normalidade gerados pelo SPSS.

Tradicionalmente, o SPSS se refere à estatística dos testes simplesmente como Estatística. Referimo-nos às estatísticas dos testes de Kolmogorov-Smirnov e de Shapiro-Wilk pelas letras D e W, respectivamente. O valor de p é expresso no SPSS como Sig. Por fim, o termo df é a abreviação de degrees of freedom (graus de liberdade, em português).
Em seguida, interpretaremos os resultados dos testes da Figura 8 para as três distribuições:
- Distribuição normal (painel esquerdo da Figura 3): os testes de Kolmogorov-Smirnov, D(300) = 0,03, p = 0,20, e de Shapiro-Wilk, W(300) = 0,99, p = 0,31, indicaram que os dados não diferem de uma distribuição normal;
Distribuição qui-quadrado (painel central da Figura 3): os testes de Kolmogorov-Smirnov, D(300) = 0,27, p < 0,001, e de Shapiro-Wilk, W(300) = 0,60, p < 0,001, atingiram significância estatística, indicando, portanto, que os dados se afastam de uma distribuição normal;
Distribuição uniforme (painel direito da Figura 3): os testes de Kolmogorov-Smirnov, D(300) = 0,08, p < 0,001, e de Shapiro-Wilk, W(300) = 0,94, p < 0,001, produziram resultados significativos. Em outras palavras, eles indicaram que o pressuposto de normalidade não foi acatado nesses dados.
Em síntese, os dois testes indicaram que o pressuposto de normalidade foi violado nas distribuições qui-quadrado e uniforme, mas não na distribuição normal.
Os testes citados neste tutorial, assim como os testes de hipótese de assimetria e de curtose da seção anterior, têm um problema em comum. Se a amostra for muito grande, eles tendem a rejeitar a hipótese nula, mesmo quando há apenas pequenos (e inconsequentes) desvios dos dados à distribuição normal. Portanto, para amostras grandes, devemos usar outros métodos além destes para avaliar a distribuição, como a análise de gráficos Q-Q.
Conclusão
Neste post, ensinamos você a avaliar a normalidade dos dados no SPSS. Por meio de três exemplos de distribuições, mostramos como interpretar os resultados de diferentes índices e testes gerados pelo SPSS.
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Kline, R. B. (2016). Data preparation and psychometrics review. In R. B. Kline, Principles and practice of structural equation modeling (4th ed., pp. 64–96). The Guilford Press.
Como citar este post
Lima, M. (2024, 3 de dezembro). Como avaliar a normalidade dos dados no SPSS? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/avaliando-a-normalidade-dos-dados-no-spss













