Neste post, apresentaremos um tutorial de como realizar e interpretar o teste de Mann-Whitney no SPSS. Então, sem mais delongas, vamos começar!
O que é o teste de Mann-Whitney?
O teste de Mann-Whitney é o equivalente não paramétrico do teste t para amostras independentes. Em outras palavras, ele pode ser usado para comparar diferenças entre duas medidas independentes, usando os postos como desfecho do modelo estatístico.
Mas o que são postos? Em síntese, eles consistem em transformações da métrica original de nossa variável dependente. Por exemplo, suponha que temos os seguintes escores, 500, 45, 60, 15, 30. Para transformá-los em postos, nós primeiramente reordenamos os escores em sequência ascendente, 15, 30, 45, 60, 500 e, em seguida, atribuímos o posto 1 ao menor escore, o posto 2 ao segundo menor, e assim sucessivamente. A Figura 1 ilustra essa transformação.
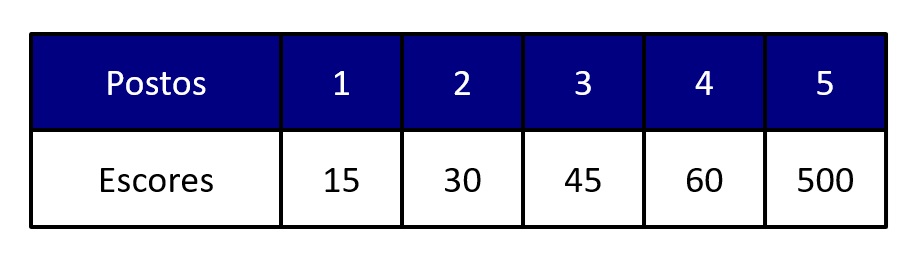
Os postos representam uma transformação ordinal. Em outras palavras, eles mantêm o ranqueamento relativo dos escores originais, mas não preservam necessariamente suas distâncias. Por exemplo, enquanto a diferença entre os escores 60 e 500 é de 440 pontos, a distância entre seus postos é de apenas uma unidade. Além disso, essa mesma distância de uma unidade se aplica a todos os postos adjacentes (como os postos 3 e 4), mesmo que as distâncias entre os escores originais variem consideravelmente. Por exemplo, a distância entre os escores 45 e 60 é de apenas 15 pontos.
Algumas perguntas que podem ser respondidas por meio do teste de Mann-Whitney incluem:
- Há diferenças na satisfação conjugal de pessoas com e sem filhos?;
- Os níveis de estresse ocupacional diferem entre trabalhadores em regime presencial e remoto?;
- Existem diferenças no desempenho acadêmico entre estudantes de escolas públicas e privadas?;
- Os níveis de ansiedade diferem entre indivíduos que praticam yoga e aqueles que não praticam?
Desse modo, o teste de Mann-Whitney é útil para responder a uma ampla gama de perguntas de pesquisa.

Como realizar o teste de Mann-Whitney no SPSS?
Exemplo
Suponha que questionamos cinco homens e seis mulheres qual foi o valor que eles gastaram no último presente de Dia das Mães. A Figura 2 ilustra o banco de dados baseado nesse exemplo. A coluna sexo representa o sexo biológico de cada participante (1 = masculino; 2 = feminino), enquanto a coluna presente representa o valor, em reais, gasto por cada respondente.

Sendo assim, podemos formular as seguintes hipóteses:
- Hipótese nula (H0): a probabilidade do valor gasto por um homem aleatoriamente selecionado ser maior que o de uma mulher aleatoriamente selecionada é igual à probabilidade do valor gasto por uma mulher aleatoriamente selecionada ser maior que o de um homem aleatoriamente selecionado;
- Hipótese alternativa (H1): a probabilidade do valor gasto por um homem aleatoriamente selecionado ser maior que o de uma mulher aleatoriamente selecionada é diferente da probabilidade do valor gasto por uma mulher aleatoriamente selcionada ser maior que o de um homem aleatoriamente selecionado.
Em seguida, o teste de Mann-Whitney testará o quão discrepante a estatística do teste é do valor esperado sob a hipótese nula. A rejeição da hipótese nula ocorrerá considerando um nível de significância de 5%, ou seja, α = 0,05.
Solicitando estatísticas descritivas
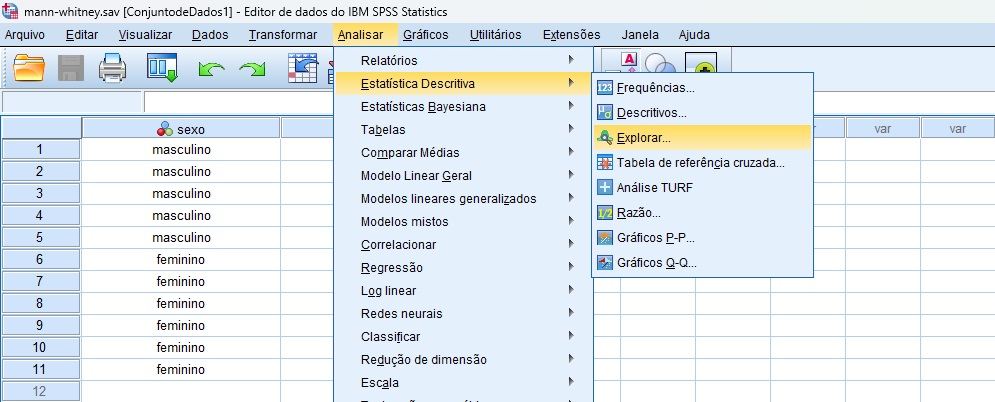
Antes de mais nada, é importante solicitar algumas estatísticas descritivas, pois elas são essenciais para auxiliar na interpretação dos resultados. Para gerar essas estatísticas, siga o seguinte caminho: Analisar > Estatística Descritiva > Explorar (Figura 3).
Em seguida, na janela Explorar, insira a variável presente na Lista de Variáveis Dependentes, e a variável sexo na Lista de fatores (Figura 4).
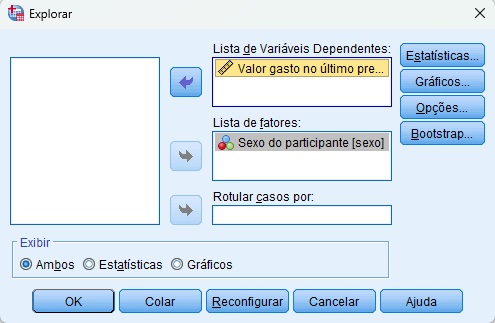
Por fim, para obter os resultados, clique em OK.
Solicitando o teste de Mann-Whitney no SPSS
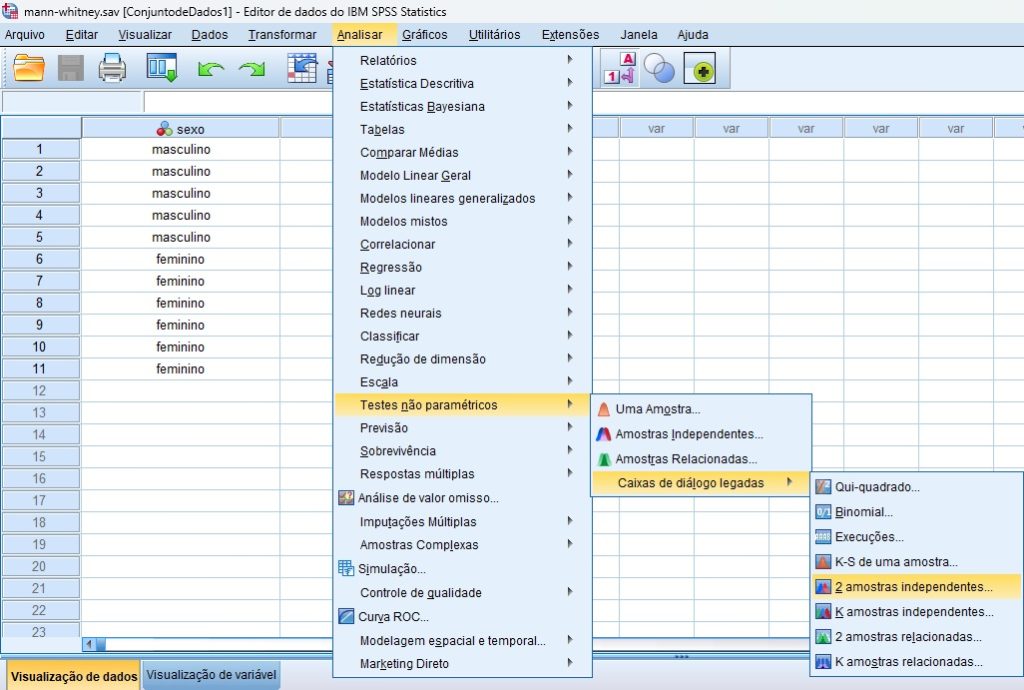
Antes de interpretarmos as estatísticas descritivas, também será necessário solicitar o teste de Mann-Whitney. Primeiramente, siga o caminho Analisar > Testes não paramétricos > Caixas de diálogo legadas > 2 amostras independentes (Figura 5).
Na janela que abrirá, insira a variável presente em Lista de variáveis de teste, pois é essa variável que queremos avaliar. Além disso, insira a variável sexo em Variável de agrupamento (Figura 6), e clique em Definir grupos.
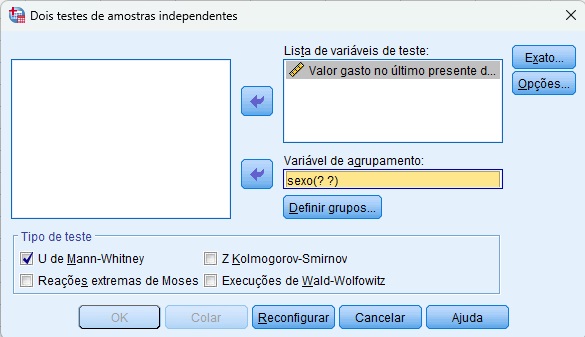
Em seguida, você deve informar ao SPSS quais são os códigos numéricos atribuídos aos níveis da variável grupo. Entretanto, aqui você poderia se perguntar, “se temos apenas dois grupos, por que precisamos especificar essa informação?”. O motivo disso é porque você poderia inserir uma variável multicategórica (i.e., com 3 ou mais níveis), mas querer comparar apenas dois desses níveis. Desse modo, seria necessário explicitar ao SPSS quais categorias devem ser comparadas em sua análise.
Conforme mencionado anteriormente, nossos grupos foram definidos como 1 = masculino e 2 = feminino. Sendo assim, será necessário inserir os valores 1 e 2 nos campos Grupo 1 e Grupo 2, respectivamente. Em seguida, clique em Continuar (Figura 7).
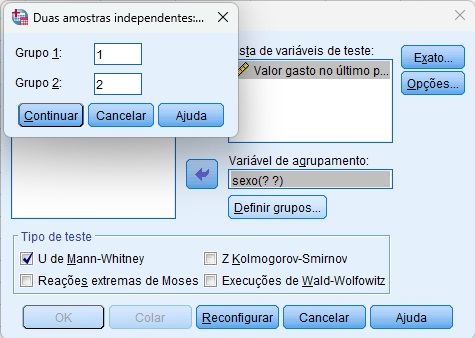
Para concluir, clique em OK.
Interpretando a saída do teste de Mann-Whitney no SPSS
Estatísticas descritivas
A Figura 8 apresenta as estatísticas descritivas geradas pela janela Explorar. Editamos essa saída do SPSS, de modo a deixá-la mais enxuta, apenas com as informações mais relevantes para nossa análise. Scheff (2016) recomenda o relato de medianas e da amplitude dos dados, isto é, valores mínimos e máximos, como estatísticas descritivas.
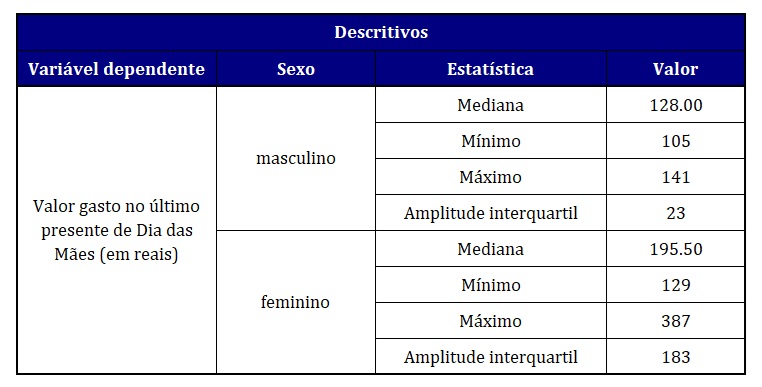
Como alternativa, você pode optar por reportar a amplitude interquartílica em vez dos valores mínimos e máximos. Essa estatística, que é uma medida de dispersão, considera a diferença entre os quartis 3 e 1, compreendendo, portanto, 50% dos dados em seus limites. De qualquer forma, as estatísticas descritivas mostram que os valores gastos foram tanto mais elevados quanto mais variáveis entre mulheres do que entre homens.
Estatísticas inferenciais
Em seguida, fazemos uma breve avaliação das estatísticas dos postos, fornecidas quando solicitamos o teste de Mann-Whitney (Figura 9). Essa tabela indica os tamanhos dos grupos (N), a média dos postos por grupo (Posto Médio) e a soma dos postos (Soma de Classificações). Note que soma dos postos = média dos postos × N.
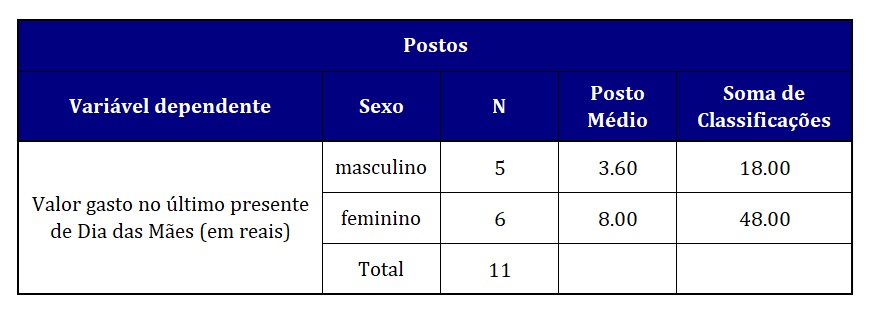
O teste de Mann-Whitney usa os postos em seus cálculos, mas essas informações são difíceis de interpretar. Contudo, podemos concluir, com base na Figura 9, que os postos médios dos homens foram bem mais baixos (3,60) que os das mulheres (8,00), indicando que os gastos das mulheres foram mais elevados em relação aos dos homens.
Por fim, interpretaremos a tabela que apresenta a estatística do teste (Figura 10). A estatística U de Mann-Whitney é o principal cálculo realizado pelo teste. Com base nesse valor, é possível convertê-lo em um escore z, que pode ser interpretado como uma estimativa padronizada da discrepância entre o valor U obtido e o valor esperado sob a hipótese nula. Além disso, o escore z possui um valor de probabilidade associado, identificado pela linha Sig exata [2(Sig. de 1 extremidade)].
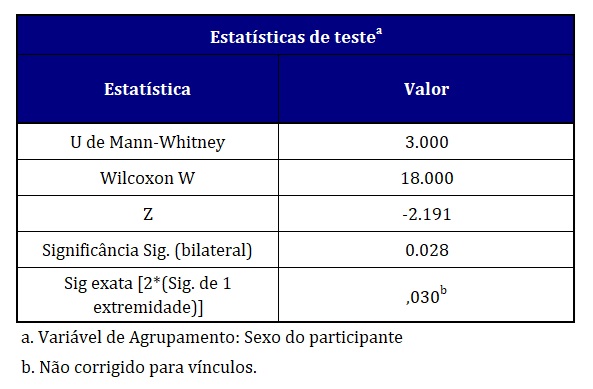
Nosso teste produziu um resultado estatisticamente significativo, ou seja, um valor de p (0,03) menor que o nosso nível de significância (0,05). Desse modo, rejeitaremos a hipótese nula e consideraremos que mulheres gastaram valores significativamente maiores que homens no último presente de Dia das Mães.
Reportando os resultados das análises do teste de Mann-Whitney
Embora o teste de Mann-Whitney não seja de medianas, podemos reportar medianas e amplitudes nos resultados, para fins de caracterização descritiva dos grupos, conforme sugerido por Scheff (2016). Além disso, é relevante reportarmos os tamanhos grupais, a estatística U e/ou escore z, o valor de p. Adicionalmente, Field (2017) recomenda acrescentar uma medida de tamanho de efeito nos resultados.
Em nosso exemplo, a medida de tamanho de efeito será o r, que foi igual a 0,66. Contudo, para não nos alongarmos, explicaremos como calcular essa medida em outro post.
Desse modo, os resultados descritos a seguir servem como sugestão de redação:
Homens relataram menores gastos com presentes no último Dia das Mães (Mdn = 128 reais, amplitude = 105–141, n = 5) do que mulheres (Mdn = 195,50 reais, amplitude = 129–387, n = 6). O teste de Mann-Whitney identificou diferenças significativas entre os grupos, U = 3, z = 2,19, p = 0,03, r = 0,66, o que indicou um efeito grande, segundo as diretrizes sugeridas por Cohen (1988).
Conclusão
Neste post, você aprendeu a realizar o teste de Mann-Whitney no SPSS. Além disso, apresentamos uma breve sugestão de como relatar os resultados dessa análise estatística. Para aprender a calcular o tamanho de efeito, que foi apresentado em nossa descrição dos resultados, veja este post.
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Academic press.
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Scheff, S. W. (2016). Nonparametric statistics. In S. W. Scheff (Ed.), Fundamental statistical principles for the neurobiologist : A survival guide (pp. 157–182). Elsevier. https://doi.org/10.1016/B978-0-12-804753-8.00008-7
Como citar este post
Lima, M. (2024, 11 de dezembro). Como executar o teste de Mann-Whitney no SPSS? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/como-executar-o-teste-de-mann-whitney-no-spss













