Neste post, falaremos sobre a análise de variância (ANOVA). Mais especificamente, descreveremos brevemente quando usar a ANOVA. Em seguida, discorreremos sobre a lógica dos cálculos da ANOVA. Por fim, apresentaremos um tutorial de como realizar essa análise no JASP.
Quando usar a análise de variância?
A fim de investigarmos se os grupos A e B diferem em função de uma variável dependente, podemos comparar os grupos por meio de um teste t para amostras independentes.
Em contrapartida, quando temos mais grupos (e.g., grupos A, B, C, D), não conseguimos compará-los usando o teste t. A fim de compararmos múltiplos grupos, precisaremos usar a ANOVA, que compara as médias de três ou mais grupos ou condições.
Usamos ANOVA, por exemplo, para comparar os escores de ansiedade por faixa etária. Sendo assim, teríamos uma variável categórica, com três níveis (e.g., jovens adultos, adultos e idosos) e uma variável contínua (e.g., ansiedade), que seria objeto de nossa comparação.
Mas por que simplesmente não realizar várias comparações pareadas? Se houver quatro grupos (A, B, C, D), por exemplo, e as diferenças forem comparadas usando testes t múltiplos, teríamos seis comparações possíveis:
- Grupo A vs. Grupo B.
- Grupo A vs. Grupo C.
- Grupo A vs. Grupo D.
- Grupo B vs. Grupo C.
- Grupo B vs. Grupo D.
- Grupo C vs. Grupo D.
Se definirmos um nível de significância de 0,05, então a probabilidade de erro Tipo I é de 5%. No entanto, com comparações múltiplas, se assumirmos independência entre os testes, a probabilidade de cometer ao menos um erro Tipo I será equivalente a:

onde FWER se refere ao familywise error rate, ou seja, à probabilidade de pelo menos um erro Tipo I em uma série de testes.
Em outras palavras, se as hipóteses nulas de todos os testes forem verdadeiras, ainda assim haverá a probabilidade de 26% de erroneamente rejeitarmos ao menos uma delas. Uma maneira de contornar esse problema é conduzindo um teste global (a ANOVA) seguido de testes post hoc, que fazem comparações múltiplas aplicando correções para o número de testes conduzidos.

Como calcular a análise de variância?
Na ANOVA, particionamos a variabilidade presente em nossa variável dependente em diferentes componentes. O objetivo é identificar e quantificar fontes distintas de variância presentes nos dados.
Primeiramente, consideramos a variabilidade total em nossos dados, operacionalizada como a soma dos quadrados dos desvios de cada escore individual em relação à média geral da amostra (SST).
Em seguida, podemos particionar essa variância em duas fontes distintas: (a) a variância explicada pelo nosso modelo (i.e., por nossa variável categórica), que consiste na soma dos quadrados dos desvios da média de cada grupo em relação à média geral (SSW); e (b) a variância não explicada pelo nosso modelo (i.e., variância não sistemática), que consiste na soma dos quadrados dos desvios de cada escore individual em relação a sua respectiva média grupal (SSB).
Como cada componente de variância considera um número distinto de observações, calculamos suas médias, de modo a torná-las comparáveis. Para calcular as médias, dividimos cada SS por seus respectivos graus de liberdade. A Figura 1 apresenta as fórmulas de cada cálculo.

Por fim, calculamos a estatística F, que consiste na razão entre MSW e MSB. Essa razão expressa a variação explicada pelo modelo estatístico e a variação atribuível a fatores não sistemáticos. Se a variância entre grupos for maior que a variância dentro dos grupos (denotado por uma estatística F mais elevada), então teremos evidências de que os grupos provavelmente diferem entre si.
Mas não se assuste, a ANOVA é um teste bastante difundido, e você pode executá-lo em inúmeros softwares estatísticos, sem precisar realizar cálculos à mão! Inclusive, neste post, vamos ver um tutorial de como executar e como interpretar a tabela da ANOVA.
Como realizar a análise de variância no JASP?
Descrição do banco de dados
Este tutorial se baseia no manual de Goss-Sampson (2020), disponível gratuitamente para download no site do JASP. Além disso, usaremos um banco de dados mencionado nesse manual, também publicamente disponível (download).
Em síntese, o banco de dados Independent ANOVA diets.csv contém a coluna Diets, que representa três tipos distintos de dietas que queremos contrastar (A, B e C), e a coluna Weight loss kg, que representa a quantidade absoluta de perda de peso após 8 semanas em uma das dietas. A Figura 2 ilustra o banco de dados aberto no JASP.
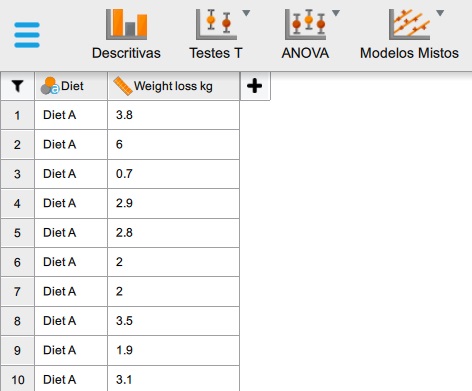
Solicitando a análise de variância no JASP
Após fazer o download do banco de dados e abri-lo no JASP, siga o caminho ANOVA > Clássico > ANOVA (Figura 3).

Em seguida, insira Weight loss kg na caixa Variável Dependente, e a variável Diet em Fatores Fixos. Na guia Exibir, marque as opções Descritivas, Estimativas de tamanho de efeito (η2 e ω2), conforme ilustrado na Figura 4.

Posteriormente, temos que checar os pressupostos da ANOVA de uma via. A variável independente deve ser categórica e a variável dependente deve ser contínua. Além disso:
- Os grupos devem ser independentes entre si.
- A variável dependente deve ter distribuição aproximadamente normal.
- Não deve haver outliers significativos.
- Deve haver homogeneidade das variâncias entre os grupos; caso contrário, o valor de p para a estatística F pode não ser confiável.
O primeiro pressuposto geralmente é controlado por meio do uso de um delineamento de pesquisa apropriado. Se o pressuposto de normalidade for violado, podemos aplicar a correção da ANOVA de Welch. No entanto, se os três últimos pressupostos da lista anterior forem violados de forma cumulativa, o equivalente não paramétrico, o teste de Kruskal-Wallis, deve ser considerado.
Para avaliarmos os pressupostos, marcaremos, na aba Verificação de Pressupostos, as opções Testes de Homogeneidade, Correções de Homogeneidade (Nenhuma e Welch) e Gráfico Q-Q dos resíduos (Figura 5).

Automaticamente, o JASP irá gerar três tabelas e o gráfico Q-Q dos resíduos.
Como interpretar as saídas da análise de variância no JASP?
A Figura 6 apresenta a tabela principal da ANOVA.

A tabela principal da ANOVA mostra que a estatística F é significativa (p < 0,001) e que existe um tamanho de efeito (ω2) grande. Portanto, existe uma diferença significativa entre as médias dos três grupos de dieta. Mas agora você pode estar se perguntando: qual linha devo me basear para reportar tal resultado?
Para responder a essa pergunta, temos que checar o pressuposto da homogeneidade e assim saber qual linha devemos reportar. O pressuposto de homogeneidade das variâncias é checado por meio do teste de Levene (Figura 7).
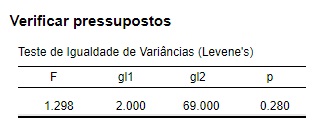
Em nosso exemplo, o teste de Levene produziu um resultado não significativo, o que não nos permite rejeitar o pressuposto de homogeneidade das variâncias. Sendo assim, interpretaremos a linha None (nenhuma), na Figura 6. No entanto, se o teste de Levene tivesse sido significativo, interpretaríamos a linha Welch (Figura 6).
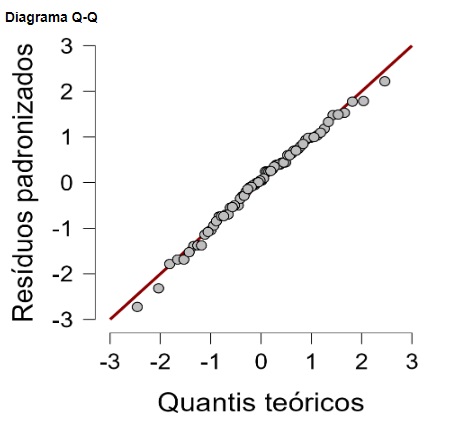
O gráfico Q-Q mostra que os dados parecem ser normalmente distribuídos e lineares (Figura 8). Isso ocorre porque a distribuição bivariada dos pontos caem sobre a reta bissetriz, de acordo com o que seria esperado no caso de normalidade nos dados.
Por fim, as estatísticas descritivas sugerem que a Dieta C resultou na maior perda de peso após 8 semanas, seguida da Dieta B, e depois da Dieta A (Figura 9).

Todavia, ainda não sabermos se essas diferenças são estatisticamente significativas. Em seguida, para obtermos essa resposta, conduziremos testes post hoc.
Solicitando e interpretando os testes post hoc
Como vimos, a tabela principal da ANOVA mostrou que a estatística F foi significativa. Mas quais grupos diferem entre si? Embora a Figura 9 forneça medidas descritivas das diferenças entre grupos, queremos avaliar, do ponto de vista inferencial, em quais diferenças entre grupos podemos confiar.
O teste post hoc aborda diretamente essa questão. Na aba Testes Post Hoc, adicione Diet à caixa de análise à direita. Em seguida, marque as opções Tipo Padrão; Tamanho de efeito, para obtermos o d de Cohen; Tukey, para a correção post hoc; e Sinalizar comparações significantes, para facilitar nossa visualização de quais contrastes produziram diferenças significativas (Figura 10).

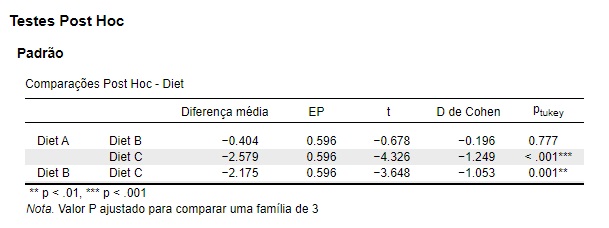
Os resultados do teste post hoc são apresentados na Figura 11. Como podemos ver nessa saída, a Dieta C difere significativamente das duas demais dietas; por outro lado, as demais dietas não diferem entre si. Os valores dos ds de Cohen sugerem um grande tamanho de efeito da Dieta C sobre a perda de peso, quando comparada às Dietas A e B.
Como reportar os resultados da análise de variância?
Em seguida, apresentamos uma sugestão de relato dos resultados da ANOVA que realizamos no JASP. Entre colchetes, apresentamos o número da figura, tal como numerada neste post, na qual baseamos cada uma de nossas afirmações.
O teste de Levene indicou que não houve heterocedasticidade significativa da perda de peso em função dos três tipos de dietas, F(2, 69) = 1,30, p = 0,28 [Figura 7]. Além disso, o gráfico Q-Q sugeriu boa aderência dos dados a uma distribuição normal teórica [Figura 8], de modo que a realização da ANOVA se mostrou apropriada.
Sendo assim, realizamos uma ANOVA com a dieta (A, B, C) como variável de agrupamento e a perda de peso como variável dependente. A ANOVA indicou diferenças na perda de peso após oito semanas, F(2, 69) = 10,83, p = 0,001, ω2 = 0,21 [Figura 6].
Comparações post hoc usando a correção de Tukey revelaram que a Dieta C resultou em perda de peso significativamente maior (M = 5,59 kg, DP = 2,11) do que a Dieta A (M = 3,01 kg, DP = 1,67), t = 4,33, pTukey < 0,001, d = 1,25; e do que a Dieta B (M = 3,41 kg, DP = 2,36), t = 1,05, pTukey = 0,001, d = 1,05. Os tamanhos de efeito nessas comparações foram grandes [Figura 11].
Por fim, a Dieta B levou a uma perda de peso maior que a Dieta A, mas esse efeito foi pequeno e não estatisticamente significativo, t = 0,68, p = 0,78, d = 0,20 [Figura 11].
Conclusão
Esperamos que, com este tutorial, tenha ficado claro para você o que é e como realizar uma ANOVA no JASP. Gostou desse conteúdo? Então aproveite e se inscreva em nosso canal do YouTube para ficar por dentro de nossas novidades!
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Goss-Sampson, M. A. (2020). Statistical analysis in JASP: A guide for students (4th ed.). https://doi.org/10.6084/m9.figshare.9980744
Como citar este post
Lima, M., & França, A. (2025, 26 de fevereiro). Como realizar a análise de variância no JASP? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/como-realizar-a-analise-de-variancia-anova-no-jasp/
* Versão original escrita por Alex França e posteriormente revisada e adaptada por Marcos Lima.













