A análise paralela é um método de simulação Monte Carlo usado para decidir qual o número de fatores extrair de um conjunto de dados. Neste post, descreveremos as etapas da análise paralela. Além disso, também recomendaremos um vídeo sobre como executar a análise paralela da maneira correta.
Etapas da análise paralela
O objetivo da análise fatorial exploratória é explicar, por meio de um número menor de fatores, a maior parte da variância comum observada nas variáveis originais. Desse modo, pesquisadores precisam decidir o número de fatores a extrair, a fim de obter soluções fatoriais parcimoniosas, com plausibilidade teórica e, ao mesmo tempo, com bom poder explicativo.
Uma das técnicas usadas para informar pesquisadores sobre o número de fatores a reter é a análise paralela. Na análise paralela, nós geramos matrizes de correlações aleatórias não correlacionadas, considerando os mesmos números de respondentes (n) e de itens (p) que os existentes em nosso banco de dados original. Essas matrizes representam um modelo nulo, isto é, em que a matriz de correlações não é fatorável.

Em cada repetição, realizamos a decomposição de nossa matriz aleatória, extraindo os eigenvalues e armazenando esses valores obtidos. Em síntese, cada eigenvalue expressa a variância comum a um conjunto de variáveis do instrumento original.
O procedimento anterior se repete centenas ou milhares de vezes, a fim de obtermos uma distribuição amostral de eigenvalues aleatórios, a partir da qual podemos calcular os eigenvalues médios associados a cada fator (de 1 até p).
Por fim, nós comparamos nossos eigenvalues empíricos, isto é, aqueles obtidos em nossos dados reais, com os eigenvalues médios aleatórios, isto é, aqueles obtidos em nossa simulação Monte Carlo.
Segundo a análise paralela, o número de fatores a extrair será o número do último eigenvalue dos dados reais maior que 1 e maior que o dos dados simulados.
Saiba mais: O que é análise paralela?

Ilustração da análise paralela
Em seguida, apresentamos um exemplo fictício, de modo a clarificar as ideias anteriormente apresentadas. Por exemplo, suponha que aplicamos um instrumento contendo oito itens em uma amostra de 1.000 respondentes. A Figura 1 compara os eigenvalues empíricos com os eigenvalues médios dos dados aleatórios, obtidos por meio da análise paralela.
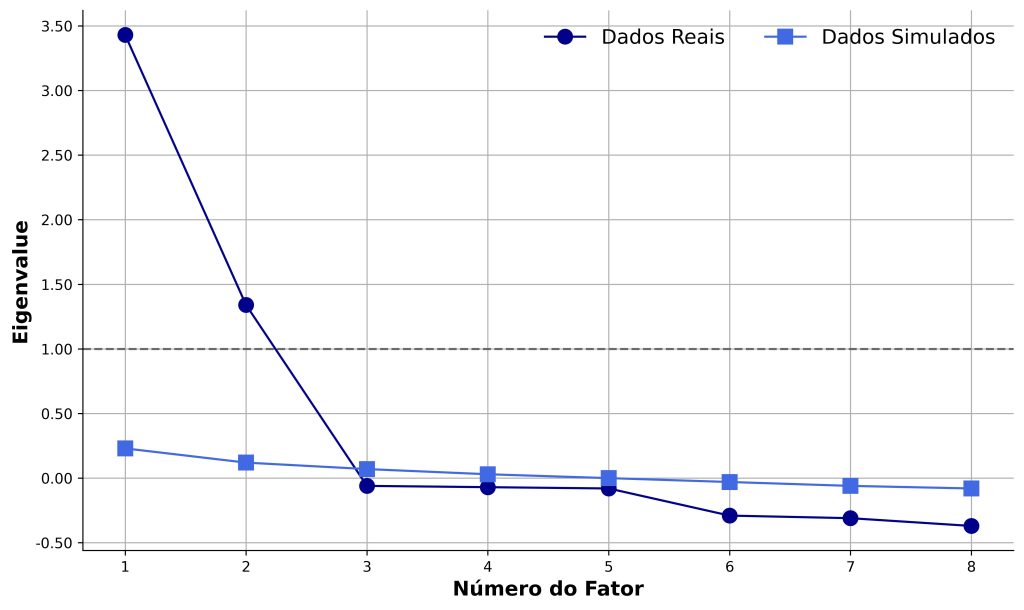
A linha pontilhada cinza da Figura 1 representa o eigenvalue = 1, que corresponde ao critério de Kaiser–Guttman, a saber, que o número de fatores a extrair será o número de fatores cujos eigenvalues são maiores que 1.
Em contrapartida, a análise paralela acrescenta um segundo critério para essa decisão, o que a torna mais exigente na determinação do número de fatores “verdadeiros”. Desse modo, segundo a análise paralela, inspecionamos qual é o último fator em que o eigenvalue empírico é maior que o eigenvalue simulado. Na Figura 1, esse é o segundo fator, pois o eigenvalue simulado passa a ser maior que o empírico a partir do terceiro fator.
Além do resultado gráfico (i.e., o scree plot da Figura 1), alguns softwares podem apresentar os resultados de forma tabular, tal como representado na Figura 2.
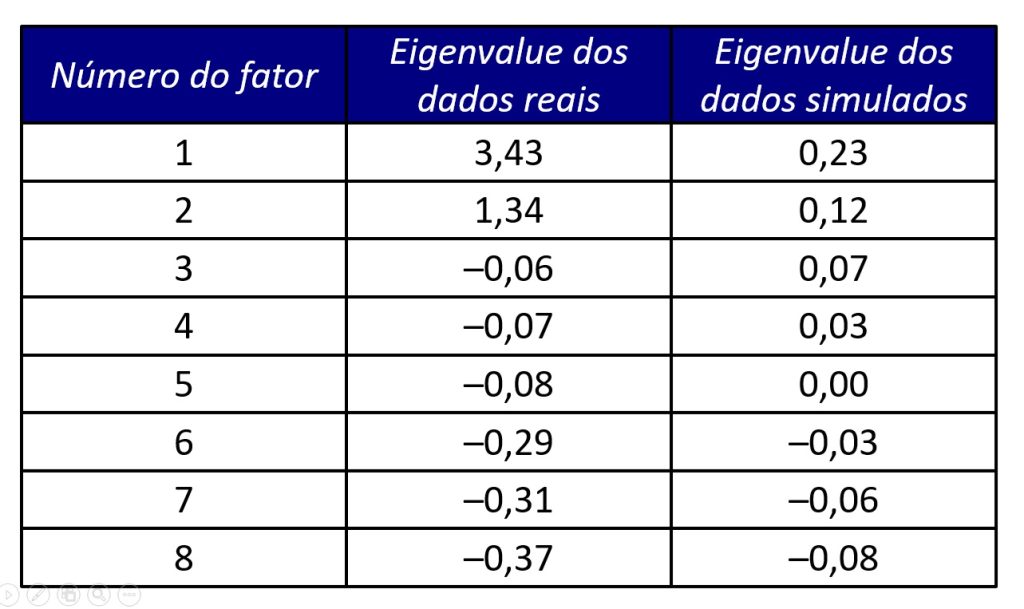
No entanto, a interpretação segue sendo a mesma: o número de fatores que devem ser retidos é de até 2 fatores, pois a partir do terceiro, os eigenvalues dos dados simulados passam a ser maiores que os eigenvalues dos dados empíricos.
Como executar a análise paralela na prática?
Em conclusão, recomendamos um vídeo que vai te mostrar exatamente como executar a análise paralela no FACTOR. Desse modo, objetivamos ajudá-lo a determinar o número de fatores para o seu instrumento. Além disso, recomendamos a leitura do tutorial de Damásio (2012), que apresenta diversas dicas sobre as melhores práticas em análise fatorial exploratória, que vão além da análise paralela.
Se você pecisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Bandalos, D. L. (2018). Measurement theory and applications for the social sciences. The Guilford Press.
Damásio, B. F. (2012). Uso da análise fatorial exploratória em psicologia. Avaliação Psicológica, 11(2), 213–228.
Como citar este post
Lima, M. (2024, 26 de dezembro). Como executar análise paralela? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/como-executar-analise-paralela/













