Neste post, você aprenderá o que é correlação tetracórica. A fim de facilitar sua compreensão, apresentaremos um exemplo simples, acompanhado de representações gráficas e tabulares. Desse modo, nosso foco é a compreensão conceitual da técnica. Esperamos, com isso, que você consiga compreender esse importante conceito da análise quantitativa de dados.
Os dados típicos de instrumentos de autorrelato
Em ciências sociais e comportamentais, é comum que pesquisadores utilizem a pesquisa por survey e instrumentos de autorrelato, a fim de investigar opiniões, atitudes, preferências, valores, traços de personalidade e sintomas dos respondentes.
Por exemplo, os respondentes podem avaliar os itens “Eu gosto de trabalhar em equipe” e “Acredito que o trabalho em equipe gera melhores resultados” por meio das alternativas “Discordo” e “Concordo”. Em tais casos, é comum que pesquisadores atribuam os valores 0 e 1 às categorias “Discordo” e “Concordo”, respectivamente.
A Figura 1 apresenta as respostas de cinco respondentes, de um banco de dados simulados com 500 casos.
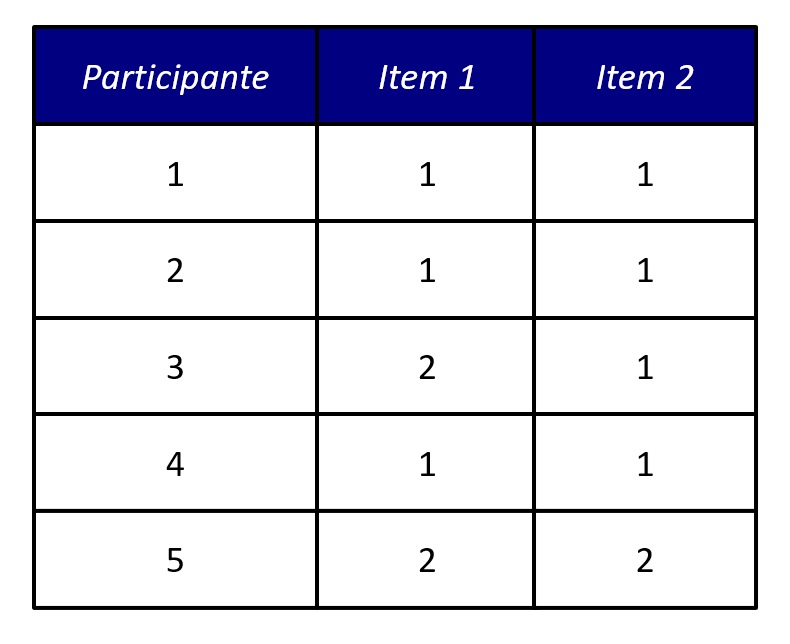
A correlação de Pearson entre as respostas de nossos 500 participantes simulados foi de 0,41. Contudo, veremos a seguir que a correlação tetracórica é mais adequada, sobretudo se assumirmos variáveis latentes subjacentes às respostas a esses itens.
O que é a correlação tetracórica?
A correlação tetracórica (rtet) é uma medida da associação entre duas variáveis dicotômicas. Ela assume que, por trás dessas variáveis observadas, existem variáveis latentes que seguem uma distribuição normal bivariada.
Em outras palavras, a correlação tetracórica tenta estimar qual seria a correlação entre as variáveis observadas se elas tivessem sido medidas de forma contínua, ao invés de dicotômica.

Qual é a lógica da correlação tetracórica?
Por exemplo, vamos considerar novamente os Itens 1 e 2 apresentados na seção anterior. Embora as respostas em nossa escala sejam dicotômicas (“Discordo” vs. “Concordo”), supomos que, por trás dessas respostas, as atitudes em relação ao trabalho em equipe sigam distribuições contínuas.
Agora, imagine que nossa amostra de 500 participantes tivesse respondido aos itens usando uma escala contínua (analógica). Nesse caso, a Figura 2 ilustra uma possível relação entre as variáveis contínuas.
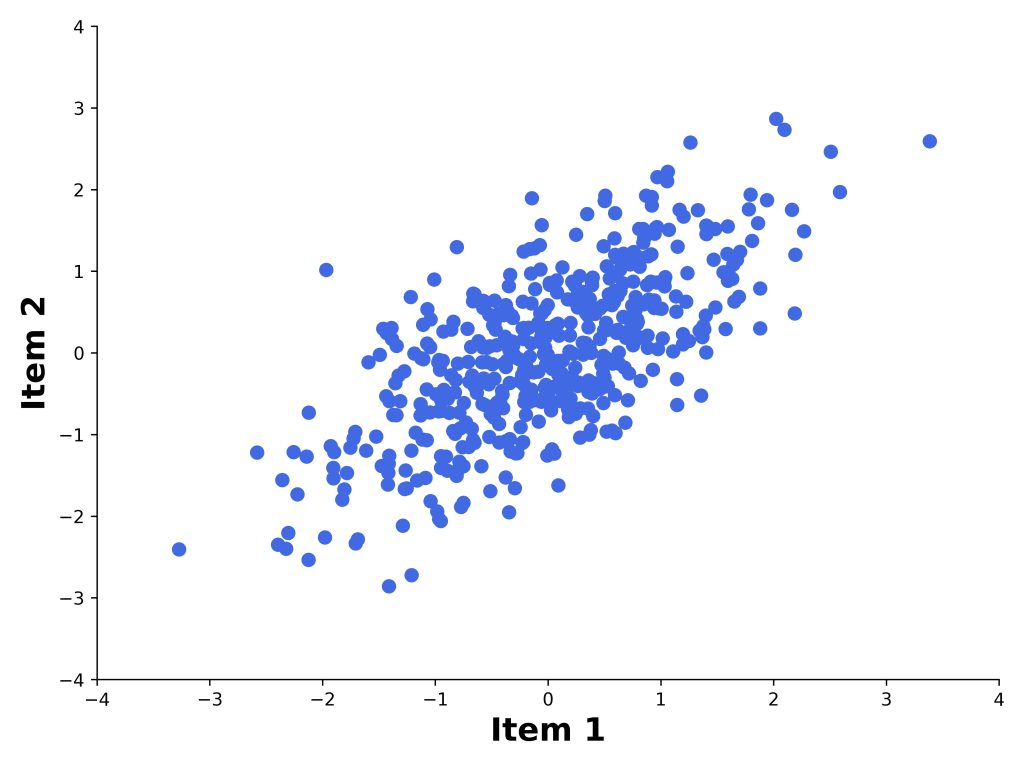
A Figura 2 sugere uma relação linear positiva entre os Itens 1 e 2. No entanto, como sabemos, as respostas foram dadas em uma escala dicotômica.
Desse modo, podemos assumir que um limiar subjacente às variáveis latentes contínuas é o que determina se o participante responde “Discordo” ou “Concordo” aos enunciados dos itens.
A Figura 3 ilustra essa ideia. Nela, plotamos as distribuições latentes contínuas subjacentes aos Itens 1 e 2. As linhas pontilhadas representam os limiares de transição entre as categorias de respostas. Um participante com um escore abaixo do limiar de um item responderá “Discordo”, enquanto um participante com um escore acima do limiar de um item responderá “Concordo”.
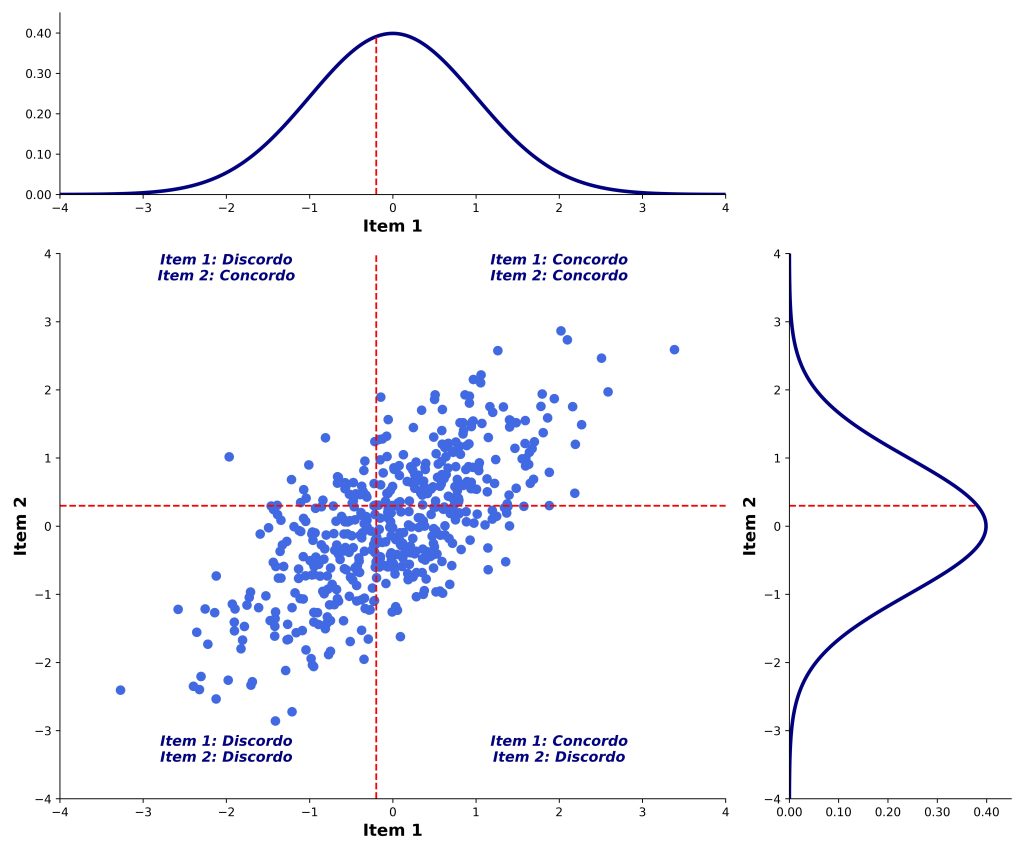
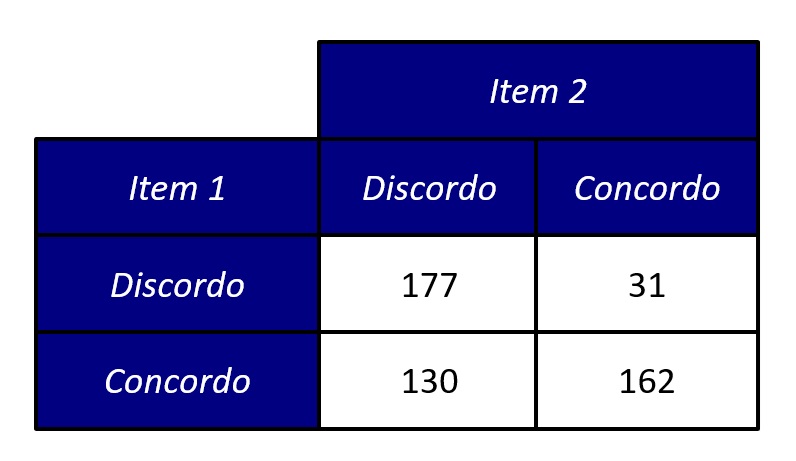
Sendo assim, o padrão contínuo, representado no diagrama de dispersão da Figura 3, resume-se a quatro quadrantes, com os padrões possíveis de respostas, indicados pelos cruzamentos de “Discordo” e “Concordo” nos Itens 1 e 2. Isso é o equivalente à tabela de contingências 2 × 2 das frequências observadas em nossos dados (Figura 4).
Qual problema a correlação tetracórica busca solucionar?
A correlação tetracórica busca estimar a correlação de Pearson entre as variáveis latentes subjacentes às respostas observadas, com base nessas respostas. Primeiramente, estimamos os limiares subjacentes às transições de respostas (em nosso exemplo, de “Discordo” para “Concordo”).
Em seguida, com base nos limiares estimados e na tabela de contingências 2 × 2, estimamos a correlação de Pearson das variáveis latentes, por meio da estimação pela máxima verossimilhança.
Por exemplo, na simulação de nossos dados, assumimos uma correlação latente entre os Itens 1 e 2 de 0,70. Contudo, nossos dados amostrais (N = 500) indicaram uma correlação ligeiramente menor, r = 0,69.
Depois disso, dicotomizamos nossas variáveis, a fim de simular os padrões de respostas dicotômicas dos participantes. A correlação de Pearson entre essas variáveis foi de 0,41, isto é, o baixo número de categorias atenuou nossa estimativa.
Por outro lado, usando a correlação tetracórica, obtivemos uma estimativa de rtet = 0,63, que foi uma estimativa muito mais próxima do valor populacional original (rho = 0,70), que aquela usando a correlação de Pearson.
Qual é a utilidade da correlação tetracórica?
Em psicometria, variáveis dicotômicas são frequentemente usadas para medir traços psicológicos. Esses traços, como neuroticismo ou extroversão, são comumente considerados como variáveis latentes contínuas, que seguem uma distribuição normal.
A correlação tetracórica, então, quantifica o grau de associação entre essas variáveis dicotômicas, assumindo que, subjacentes a essas medidas, temos variáveis latentes contínuas. Em outras palavras, a correlação tetracórica é útil para estimar qual seria a correlação entre essas variáveis se fossem medidas de forma contínua e com distribuições normais bivariadas.
Além disso, a correlação tetracórica é amplamente utilizada em análise fatorial com dados ordinais, pois ela permite substituir a matriz de correlação de Pearson por uma matriz que reflete a associação entre as variáveis dicotômicas. Desse modo, podemos reproduzir melhor o modelo de mensuração verdadeiro em análises fatoriais.
Saiba mais: Análise fatorial exploratória ou análise fatorial confirmatória: qual escolher?

Conclusão
Neste post, você aprendeu sobre a correlação tetracórica. Recomendamos que você também conheça a correlação policórica, uma generalização da correlação tetracórica, aplicada para variáveis politômicas ordinais.
Gostou desse conteúdo? Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Holgado-Tello, F. P., Chacón-Moscoso, S., Barbero-García, I., & Vila-Abad, E. (2010). Polychoric versus Pearson correlations in exploratory and confirmatory factor analysis of ordinal variables. Quality & Quantity, 44, 153–166. https://doi.org/10.1007/s11135-008-9190-y
Olsson, U. (1979). Maximum likelihood estimation of the polychoric correlation coefficient. Psychometrika, 44(4), 443–460. https://doi.org/10.1007/BF02296207
Como citar este post
Lima, M. (2024, 31 de dezembro). O que é correlação tetracórica? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-e-correlacao-tetracorica/