Você já ouviu falar da distribuição normal? Neste post, explicaremos o que é essa distribuição, quais são suas principais características e qual sua utilidade para pesquisadores. Além disso, descreveremos o que é o escore z, como calculá-lo e como interpretá-lo. Por fim, recomendaremos dois testes estatísticos para avaliar a normalidade dos dados.
O que é distribuição normal?
A distribuição normal é a mais conhecida das distribuições de probabilidade e também uma das mais importantes em estatística. Primeiramente, ela é uma distribuição contínua e simétrica ao redor da média. Isso significa que o lado direito da distribuição é uma imagem espelhada do lado esquerdo, conforme ilustrado na Figura 1.

Nessa distribuição, a maioria dos valores tende a se agrupar ao redor da média, tal como indica a Figura 1. Por outro lado, valores que se afastam da média (para mais ou para menos) tendem a ser menos frequentes.
As caudas dessa distribuição são assintóticas, o que significa que, em uma distribuição teórica, as probabilidades tendem a zero conforme os valores da variável tendem a –∞ e a +∞ (mas nunca são genuinamente zero).
A Figura 1 representa uma distribuição normal teórica. Em contrapartida, a Figura 2 representa um conjunto de dados empíricos (simulados) que se aproximam dessa distribuição teórica. Em outras palavras, isso quer dizer que essa distribuição teórica é uma boa representação para modelar as propriedades dos dados empíricos.

Em uma distribuição perfeitamente normal, a média, a mediana e a moda terão o mesmo valor, conforme representam os picos das curvas nas Figuras 1 e 2.
Devido a essas características, a distribuição normal é frequentemente chamada de curva de sino, pois o gráfico de sua densidade de probabilidade se assemalha a um sino. Além disso, essa distribuição também é conhecida como distribuição gaussiana, em homenagem ao matemático alemão Carl Friedrich Gauss (Figura 3), que a descreveu pela primeira vez.

Para que serve a distribuição normal?
Diversos fenômenos naturais ocorrem de tal maneira que são passíveis de modelagem matemática por meio da distribuição normal.
Por exemplo, suponha que selecionamos aleatoriamente 100 indivíduos e mensuramos as variáveis altura, pressão arterial e escores em um teste de inteligência desses indivíduos. Nesses casos, esperaríamos observar que os dados de cada uma das variáveis possui distribuição aproximadamente normal.
Além disso, muitos testes estatísticos dependem de que os dados, ou os resíduos, tenham distribuição aproximadamente normal. Esses testes são comumente chamados de testes paramétricos. No entanto, quando nossos dados não apresentam distribuição normal, deveremos usar modelos estatísticos que não pressupõem normalidade dos dados, como os testes não paramétricos ou modelos lineares generalizados.
Por fim, outra utilidade da distribuição normal é que podemos usar suas propriedades conhecidas para fazer predições acerca da probabilidade de observar um valor em um dado intervalo. Para isso, utilizamos uma estatística descritiva denominada escore z, sobre a qual falaremos a seguir.

O que é o escore z?
O escore z é uma transformação dos dados obtidos, em que os escores da variável original são reexpressos em termos de desvios em relação à média, em unidades de desvio-padrão. O escore z é calculado pela seguinte fórmula:

onde xi é o escore do participante i, X-barra é a média amostral e DP é o desvio-padrão amostral.
Resumidamente, um escore z estima o quão próxima ou distante uma observação está da média amostral. Por exemplo, se z = 2, então a observação está dois desvios-padrões acima da média. Se z = –1,25, então a observação está 1,25 desvio-padrão abaixo da média. Um escore z = 0 indica que a observação é exatamente igual à média.
Qual é a relação entre escores z e a distribuição normal-padrão?
A Figura 4 representa uma distribuição normal-padrão (também chamada de distribuição z), uma distribuição normal teórica especial, cuja média é 0 e o desvio-padrão é 1.

O eixo x da Figura 4 apresenta valores de observações em unidades padronizadas (os símbolos µ e σ representam, respectivamente, a média e o desvio-padrão da distribuição normal-padrão). O valor de µ equivale a z = 0, enquanto os diferentes valores de σ indicam as distâncias de um escore z dessa média 0 (e.g., 2σ equivale a z = 2).
Os valores percentuais apresentados em diferentes faixas da distribuição indicam o percentual de casos esperados em cada faixa. Por exemplo, esperamos que 68,2% das observações estejam entre –1σ e +1σ, isto é, entre z = –1 e z = 1. De maneira similar, esperamos que 95,4% das observações estejam entre –2σ e +2σ, isto é, entre z = –2 e z = 2. O mesmo raciocínio vale para outros intervalos, inclusive valores fracionários de z (e.g., z = 0,75).
Com base nessa propriedades conhecidas da distribuição normal-padrão, somos capazes de calcular a probabilidade de um escore aleatoriamente amostrado de uma distribuição normal estar entre determinados valores. Para isso, basta transformarmos o valor ou os valores de interesse em escores z, e fazermos a comparação com base na distribuição normal-padrão.
Exemplo de cálculo do escore z
Para compreendermos melhor essa propriedade da distribuição normal-padrão, vamos usar como exemplo um teste de inteligência com média populacional igual a 100, e desvio-padrão igual a 15. Qual é a probabilidade de um indivíduo aleatoriamente selecionado dessa população obter um escore maior ou igual a 130?
Primeiramente, calcularemos o escore z equivalente a um escore absoluto de 130:
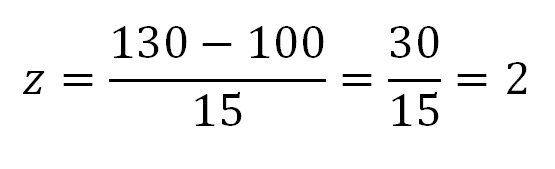
Em outras palavras, um escore absoluto de 130 no teste de inteligência, considerando-se a média e o desvio-padrão populacional, equivale a um escore 2 desvios-padrões acima da média.
Em seguida, poderíamos dizer que a probabilidade de um indivíduo aleatoriamente selecionado da população ter um escore z maior ou igual a 2 (isto é, maior ou igual a 130, na escala absoluta) equivale à soma das faixas verde e amarela direita da Figura 4: 2,1% + 0,1% ≅ 2,2%.
Embora a Figura 4 apresente apenas escores z associados a números inteiros, pacotes estatísticos computam valores de probabilidade associados a valores decimais, como –2,27, 0,35 ou 1,87. Alguns livros-textos também apresentam tabelas normativas com escores z e valores de probabilidade associados, tal como a ilustrada neste link.
Como posso avaliar a normalidade dos meus dados?
Dois testes comumente utilizados para testar o pressuposto de normalidade dos dados são os testes de Shapiro–Wilk e o teste de Kolmogorov–Smirnov. Ambos avaliam se a distribuição dos nossos dados se desvia de uma distribuição normal teórica.
Em tais testes, se o valor de probabilidade condicional não atinge significância estatística (isto é, p > 0,05), então concluímos que não temos evidência suficiente para rejeitar o pressuposto de normalidade. Para um tutorial sobre como avaliar a normalidade dos dados no SPSS, veja nosso post sobre o tema.
Saiba mais: Avaliando a normalidade dos dados no SPSS
Conclusão
Neste post, você conheceu um pouco mais sobre a distribuição normal, uma importante distribuição de probabilidades usada por estatísticos e por pesquisadores. Abordamos algumas de suas propriedades, o que são os escores z e como interpretar seus valores.
Gostou desse conteúdo? Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referência
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Como citar este post
Lima, M. (2021, 11 de maio). O que é distribuição normal? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/distribuicao-normal













