Cálculo do tamanho de efeito para o teste de Wilcoxon

Em posts anteriores, nós explicamos o que é o teste de Wilcoxon e como realizá-lo no SPSS. Neste post, daremos um passo além e mostraremos como calcular e interpretar o tamanho de efeito para o teste de Wilcoxon.

O que é o teste de Wilcoxon?

O químico e estatístico Frank Wilcoxon propôs dois testes estatísticos, mas ambos ficaram conhecidos como teste de Wilcoxon. O teste de soma dos postos de Wilcoxon avalia as diferenças entre duas amostras independentes, enquanto o teste de postos sinalizados de Wilcoxon avalia as diferenças entre duas amostras pareadas.

Visando evitar ambiguidades, preferimos nos referir ao teste de Mann–Whitney, quando nosso objetivo é comparar amostras independentes. Por outro lado, reservamos o termo teste de Wilcoxon para designar a versão pareada do teste (i.e., o teste de postos sinalizados). Por exemplo, podemos usar o teste de Wilcoxon para avaliar se há diferenças nos níveis de ansiedade percebida dos estudantes antes e após uma prova de estatística.

Desse modo, uma maneira de pensar no teste de Wilcoxon é como o equivalente não paramétrico do teste t para amostras pareadas. Ele permite a comparação dos mesmos participantes em dois momentos distintos (como no exemplo anterior), em duas condições distintas (como no exemplo que daremos na próxima seção) ou, ainda, de participantes distintos, mas emparelhados (como casais, pais e filhos ou empregadores e empregados).

Os resultados de um teste de Wilcoxon

Primeiramente, pesquisadores investigaram o desempenho dos participantes em uma tarefa psicomotora realizada após estes terem consumido água ou vodca. Todos os participantes foram expostos às duas condições. Na Sessão 1, metade dos participantes consumiu água e realizou a tarefa, enquanto na Sessão 2, esses mesmos participantes consumiram vodca antes de repetir a tarefa. A outra metade seguiu a ordem inversa: vodca na Sessão 1 e água na Sessão 2.

A Figura 1 apresenta os dados desse estudo.

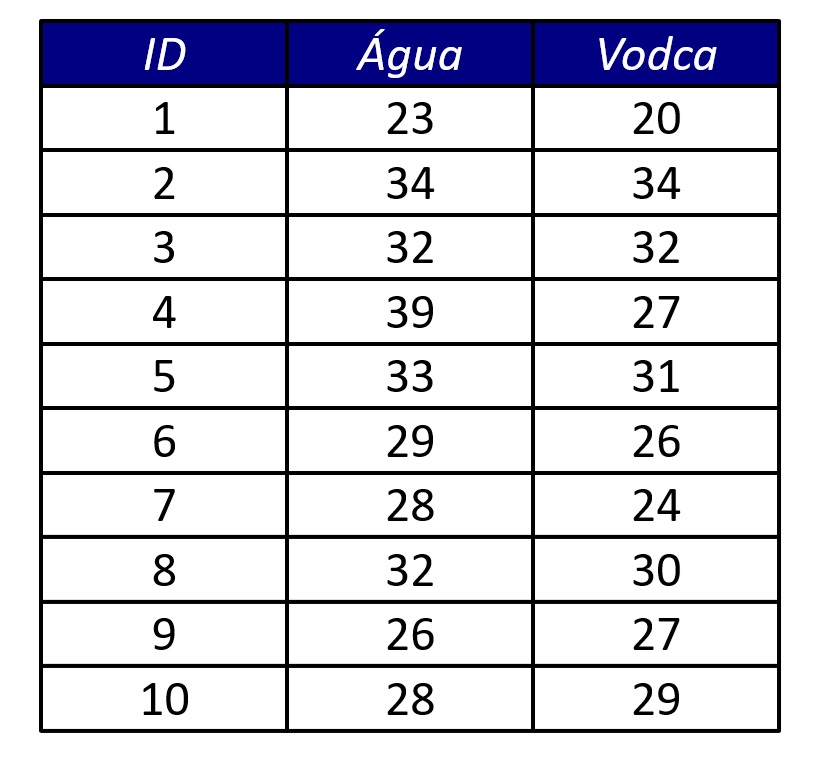
O teste de Wilcoxon, por se basear em postos, considera as diferenças pareadas positivas e negativas entre as condições. Por outro lado, o teste descarta as diferenças nulas. Por exemplo, embora o banco de dados tenha 10 participantes, dois deles (Participantes 2 e 3) tiveram escores idênticos nas duas condições. Desse modo, para fins do cálculo da estatística do teste de Wilcoxon, consideramos somente os oito casos remanescentes.

Em nosso post sobre como realizar o teste de Wilcoxon no SPSS, obtivemos z = 2,11, p = 0,035. O escore z reflete a discrepância entre a estatística do teste e o valor esperado para essa estatística considerando a hipótese nula verdadeira. Em seguida, usaremos esse escore z para calcular nossa medida de tamanho de efeito.

Como calcular o tamanho de efeito para o teste de Wilcoxon?

Rosenthal (1991, p. 28) apresenta a seguinte medida de tamanho de efeito baseada em escore z:

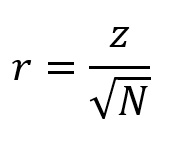
onde N se refere não ao número de casos da amostra, mas sim ao número de observações usadas no cálculo do teste de Wilcoxon. Embora a amostra em nosso exemplo fosse de 10 participantes, cada um contribuiu com duas medidas. Além disso, dois dos participantes tiveram empates (i.e., escores iguais nas condições água e vodca), de modo que eles não são considerados no cálculo do r (Field, 2017). Desse modo, N = (10 – 2) × 2 = 16. Sendo assim, podemos calcular nosso tamanho de efeito:

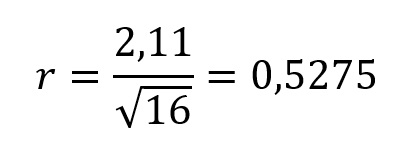
Arredondando nosso efeito em duas casas decimais, temos, portanto, r = 0,53. Cohen (1988) sugere critérios de 0,10, 0,30 e 0,50 como indicativos, respectivamente, de efeitos pequenos, médios e grandes. Desse modo, nosso efeito pode ser considerado grande.

Como reportar os resultados?

Geralmente, nós reportamos o tamanho de efeito junto ao teste estatístico apropriado. Por exemplo, no caso do teste de Wilcoxon, podemos reportar o escore z, o valor de p a ele associado e o tamanho de efeito. Além disso, Scheff (2016) recomenda a indicação do número de empates, que estima quantas observações não foram consideradas nos cálculos de z e de r. Por fim, de modo a facilitar a interpretação dos testes inferenciais, também reportaremos medianas, mínimos e máximos como estatísticas descritivas (mostramos esses cálculos em nosso post sobre como executar o teste de Wilcoxon no SPSS).

Desse modo, os resultados descritos a seguir servem como sugestão de redação:

O desempenho dos participantes na tarefa psicomotora na condição água (Mdn = 30,5, amplitude = 23–39) foi maior que na condição vodca (Mdn = 28, amplitude = 20–34). O teste de postos sinalizados de Wilcoxon indicou diferenças significativas entre condições, z = 2,11, p = 0,035, r = 0,53, um efeito considerado grande. Dois de 10 participantes tiveram desempenhos similares nas duas condições.

Conclusão

Neste post, você aprendeu a calcular o tamanho de efeito para o teste de Wilcoxon. Gostou desse conteúdo? Então aproveite e também se inscreva em nosso canal do YouTube para ficar por dentro de nossas novidades!

Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).

Referências

Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Academic press.

Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5^th ed.). Sage.

Rosenthal, R. (1991). Meta-analytic procedures for social research (2^nd ed.). Sage.

Scheff, S. W. (2016). Nonparametric statistics. In S. W. Scheff (Ed.), Fundamental statistical principles for the neurobiologist : A survival guide (pp. 157–182). Elsevier. https://doi.org/10.1016/B978-0-12-804753-8.00008-7

Wilcoxon, F. (1945). Individual comparisons by ranking methods. Biometrics, 1, 80–83.

Como citar este post

Lima, M. (2024, 5 de dezembro). Cálculo do tamanho de efeito para o teste de Wilcoxon. Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/calculo-do-tamanho-de-efeito-para-o-teste-de-wilcoxon/