Neste post, ensinaremos como calcular o escore z de uma variável no SPSS. Essa é uma técnica fundamental em estatística, pois padroniza os dados e facilita a comparação entre diferentes conjuntos de dados.
Primeiramente, descreveremos o que é e como calcular o escore z. Em seguida, apresentaremos algumas das vantagens do cálculo do escore z. Por fim, nós apresentaremos um tutorial simples e rápido de como calcular o escore z de uma variável no SPSS.

O que é e como calcular o escore z?
O escore z, também conhecido como z-score ou escore padronizado, é uma medida que expressa a quantos desvios-padrão um determinado valor está distante da média de um conjunto de dados. Em outras palavras, o escore z é uma transformação linear da variável original, onde os novos valores representam distâncias da média: valores positivos estão acima da média, enquanto valores negativos estão abaixo dela; valores iguais a zero são exatamente idênticos à média amostral.
O cálculo do escore z, também conhecido como padronização dos escores, é obtido por meio da seguinte fórmula:

onde:
- xi é o valor da observação i que você deseja padronizar;
- X-barra é a média da amostra na variável de interesse;
- DP é o desvio-padrão da amostra na variável de interesse.
Por exemplo, a Figura 1 apresenta o número de títulos mundiais obtidos por diferentes países nas Copas do Mundo FIFA de futebol masculino, no período entre 1930 e 2022. A média de títulos da Figura 1 é de 2,75 títulos, e o desvio-padrão é de 1,49.
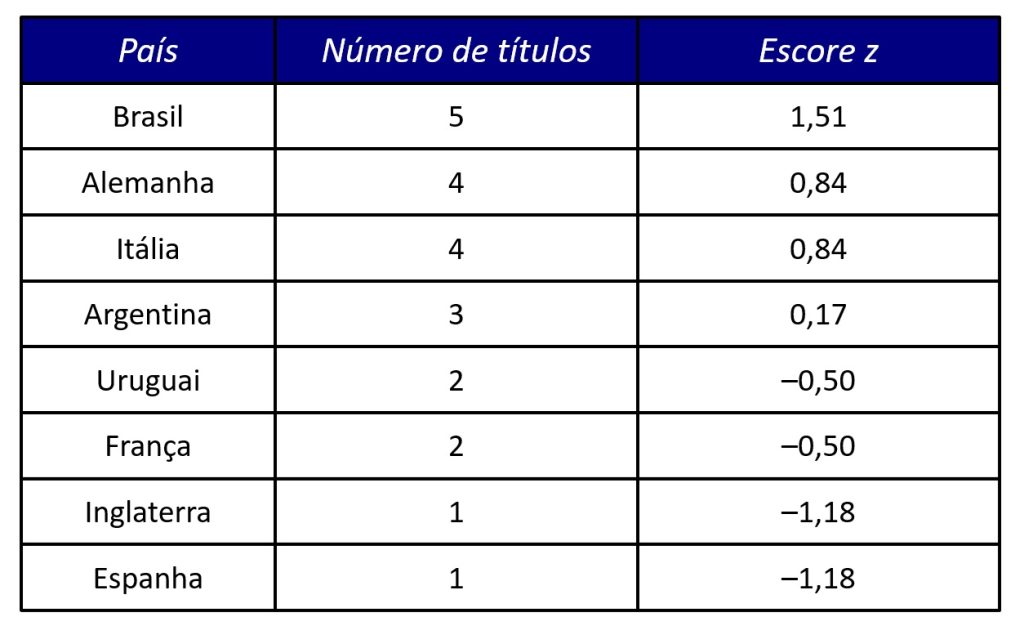
A coluna Escore z representa a variável número de títulos em unidades padronizadas. Por exemplo, no caso do Brasil, fizemos o seguinte cálculo:

onde, z = 1,51 indica que o número de títulos do Brasil está 1,51 desvio-padrão acima da média de títulos das campeãs mundiais da Figura 1. O mesmo cálculo é repetido para as demais seleções. Observe que as seleções com um número de títulos acima da média (Brasil, Alemanha, Itália e Argentina) têm escores z positivos, enquanto as seleções com um número de títulos abaixo da média (Uruguai, França, Inglaterra e Espanha) têm escores z negativos.
Veja também:
Quais são as utilidades de calcular o escore z?
O cálculo do escore z tem várias aplicações práticas em análise de dados. Em seguida, destacamos algumas de suas utilidades:
- Comparação de diferentes variáveis: ao padronizar os dados, você pode comparar valores de diferentes variáveis, mesmo que tenham unidades e escalas diferentes;
- Identificação de outliers: localizar valores que estão muito acima ou abaixo da média (outliers ou valores extremos) fica mais fácil, já que escores z maiores que 3 ou menores que –3 indicam dados atípicos;
- Padronização de dados: é uma maneira eficaz de ajustar distribuições para que sejam comparáveis em uma escala comum, especialmente útil em modelos de regressão ou análises multivariadas. Desse modo, essa padronização também é útil para algoritmos de otimização que buscam identificar o melhor conjunto de parâmetros de um modelo estatístico;
- Interpretação estatística: o escore z facilita a interpretação em termos de probabilidade, ajudando assim a entender a posição de um dado dentro da distribuição normal.
Antes de apresentarmos o tutorial, convém desfazer um mito sobre o escore z, a saber, de que ele é útil para corrigir desvios de normalidade. Isso não é verdade. A Figura 2 ilustra a ideia para um conjunto de dados com forte assimetria positiva (M = 777,94, DP = 607,41, Mdn = 623,70).

Como podemos ver na Figura 2, a forma da distribuição dos dados na escala padronizada é idêntica à forma da distribuição na escala original. A única diferença entre os paineis é no eixo x. Em outras palavras, a transformação por escore z não muda a forma da distribuição; seu único efeito sobre os dados é em deslocar a distribuição no eixo x, de modo a recentralizar a distribuição ao redor da média = 0.
Como calcular o escore z no SPSS?
A Figura 3 apresenta um banco de dados no SPSS, similar aos dados descritos na Figura 1.

Calcular o escore z no SPSS é muito simples e pode ser feito em poucos passos. Primeiramente, siga o caminho Analisar > Estatísticas descritivas > Descritivos (Figura 4).

Em seguida, transfira para a caixa Variável(is) a variável (ou as variáveis) que você deseja transformar em escore z, marque a opção Salvar valores padronizados como variáveis, e clique em OK (Figura 5).

O SPSS calculará automaticamente os escores z para as variáveis selecionadas e os salvará em novas colunas no banco de dados. Essas colunas conterão os valores padronizados, ou seja, os escores z.
A Figura 6 apresenta as estatísticas descritivas da variável original, bem como de sua transformação em escore z. Como pode ser visto, os valores da média e do desvio-padrão da variável títulos coincide com o que utilizamos anteriormente para o cálculo manual dos escores z. Por fim, ela também indica que o escore z tem média = 0 e desvio-padrão = 1. Sempre que calcularmos os escores z de uma variável, a nova medida sempre terá essa média e desvio-padrão.

Conclusão
Neste post, você aprendeu como calcular o escore z de uma variável no SPSS. Além disso, você conheceu algumas das vantagens de realizar esse cálculo, bem como um mito importante sobre uma utilidade que o escore z não possui.
Gostou desse conteúdo? Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referência
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Como citar este post
Lima, M. (2024, 25 de setembro). Como calcular o escore z no SPSS? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/como-calcular-o-escore-z-no-SPSS













