Como escolher o gráfico certo para seus dados? Quando se trata de escolher a melhor representação visual para um conjunto de dados, é importante considerar não apenas a estética e a preferência pessoal, mas também a natureza dos dados e o objetivo da análise.
Neste post, vamos discutir a importância de escolher o gráfico adequado para diferentes tipos de dados, os tipos de gráficos mais comumente usados por pesquisadores e, por fim, exemplos de uso.
Veja também: Como criar gráficos no R com o ggplot2?
Por que escolher o gráfico certo é importante?
Escolher o gráfico certo é importante porque diferentes tipos de dados requerem abordagens distintas para uma comunicação rápida e eficaz. Além disso, compreender um pouco sobre como o sistema perceptual humano funciona contribui para fazer melhores escolhas na apresentação dos gráficos.
Por exemplo, veja o gráfico de pizza da Figura 1.
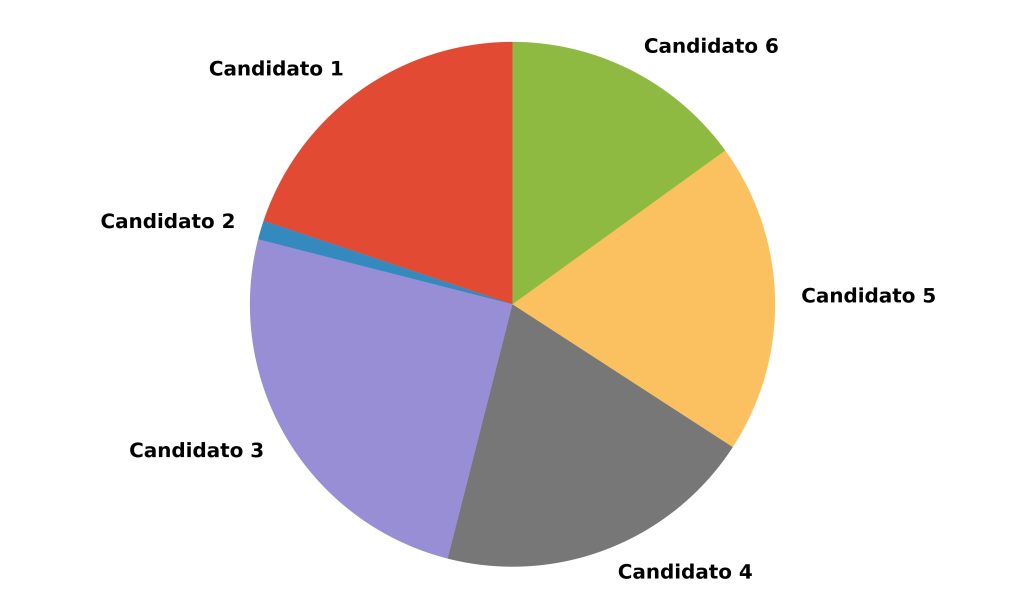
Suponha que a Figura 1 represente o percentual de intenção de voto de seis candidatos a um cargo eletivo. A partir disso, concluímos que os Candidatos 3 e 2 estão, respectivamente, em primeiro e em último lugar da corrida eleitoral. No entanto, em relação aos demais candidatos, quem está na frente?
Nosso sistema perceptual não lida bem com fatias com orientações e tamanhos distintos. No entanto, alguém poderia argumentar que basta adicionar os percentuais no gráfico para auxiliar o leitor. Embora isso ajude, ainda persistiria a dificuldade de como inserir uma medida de incerteza no gráfico de pizza, como intervalos de confiança. Claramente, o gráfico de pizza não contribui para esse tipo de representação.
Além disso, o uso de um gráfico inadequado pode atrapalhar, ao invés de auxiliar, na exposição de um argumento ou conclusão. Por exemplo, veja a Figura 2.
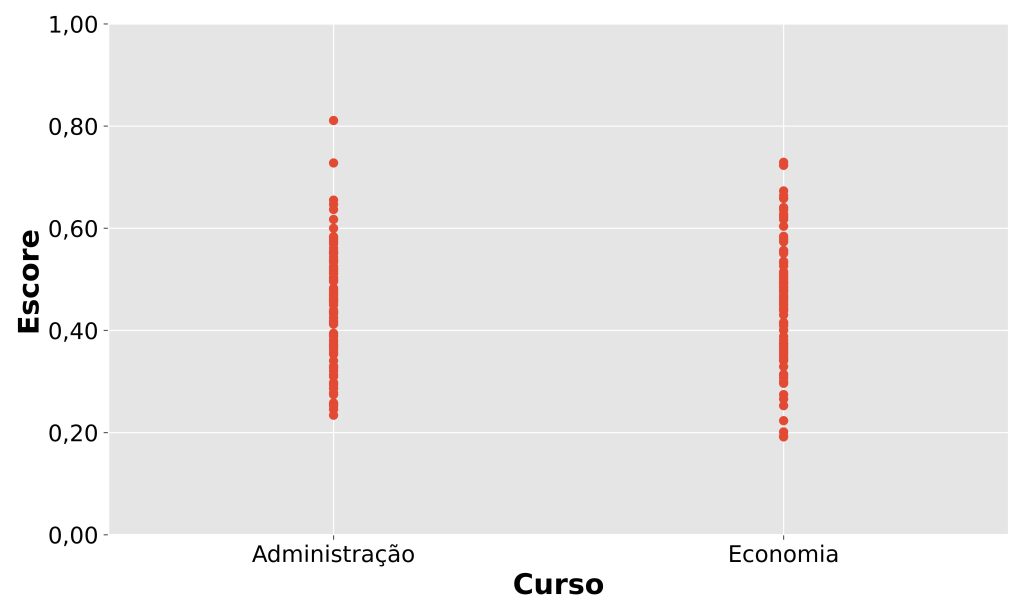
Os escores dos estudantes de administração são significativamente maiores que os escores dos estudantes de economia. Consegue visualizar isso? Provavelmente não, pois a escolha da representação gráfica desfavorece essa interpretação. Outras escolhas poderiam ser mais eficientes para essa finalidade.
Em síntese, a escolha do gráfico certo ajuda a destacar tendências, padrões e anomalias nos dados. Por exemplo, o gráfico de linhas pode ajudar a identificar tendências ao longo do tempo, enquanto um gráfico de barras pode auxiliar na comparação de quantidades entre categorias. Veremos mais sobre isso na próxima seção.
Quais são os principais tipos de gráficos que posso usar?
A escolha do gráfico certo depende da natureza dos dados e do objetivo da análise. Em seguida, apresentamos os principais tipos de gráficos e para quais tipos de dados eles são indicados.
Gráficos de barras
Os gráficos de barras são ideais para representar dados categóricos. Um gráfico de barras consiste em barras horizontais ou verticais que representam as frequências ou as proporções nas diferentes categorias.
Por exemplo, podemos utilizar um gráfico de barras para representar as estimativas de óbitos por diferentes tipos de câncer em uma população, bem como o número de filhos dos participantes de uma dada amostra (Figura 3).
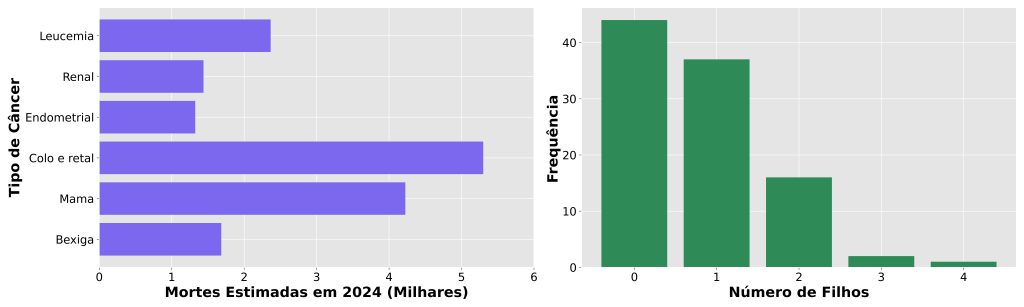
Gráficos de linhas
Os gráficos de linhas são ideais para representar dados que variam continuamente ao longo do tempo ou de uma escala. Um gráfico de linhas consiste em uma linha que conecta os pontos correspondentes aos valores dos dados em um intervalo.
Por exemplo, podemos utilizar um gráfico de linhas para representar os escores de um participante em uma tarefa comportamental ao longo dos dias do mês (Figura 4, painel esquerdo). Além disso, podemos também usar esse gráfico para representar o número de novos casos de uma doença ao longo dos meses de dois anos distintos (Figura 4, painel direito).
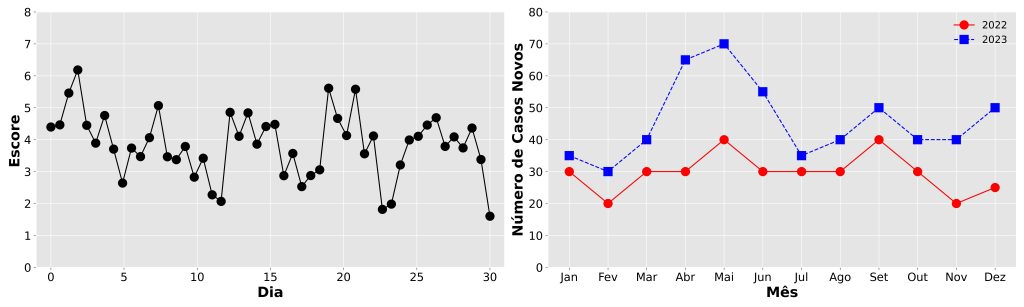
Gráficos de dispersão
Os gráficos de dispersão são ideais para representar a relação entre duas variáveis contínuas. Eles ajudam, por exemplo, a identificar variáveis que estão linearmente relacionadas. Um gráfico de dispersão consiste em um conjunto de pontos que representam os valores observados em duas variáveis.
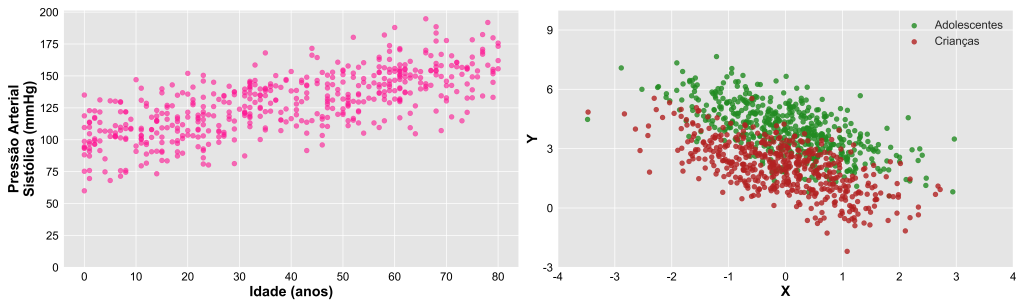
Por exemplo, podemos utilizar um gráfico de dispersão para representar a relação entre a idade e a pressão arterial sistólica em uma amostra de pacientes (Figura 5, painel esquerdo). Além disso, podemos separar os pontos em diferentes cores, símbolos ou tamanhos, a depender do pertencimento a uma dada categoria (Figura 5, painel direito).
Histogramas
Os histogramas são ideais para representar a distribuição de frequência de um conjunto de dados cuja variável de interesse é contínua. Um histograma consiste em uma série de barras verticais que representam a frequência ou a densidade de probabilidade dos dados em cada intervalo.
Contudo, para uma visualização adequada de tais gráficos, é importante que o pesquisador selecione adequadamente a largura (bin) de cada barra. Não existe uma regra geral para definir a largura de cada barra, ou seja, você precisará avaliar diferentes valores e decidir qual deles transmite as informações mais acuradas daquilo que você deseja enfatizar.
Um histograma pode ser utilizado para representar a distribuição de escores em um teste psicológico ou clínico (Figura 6, painel esquerdo).
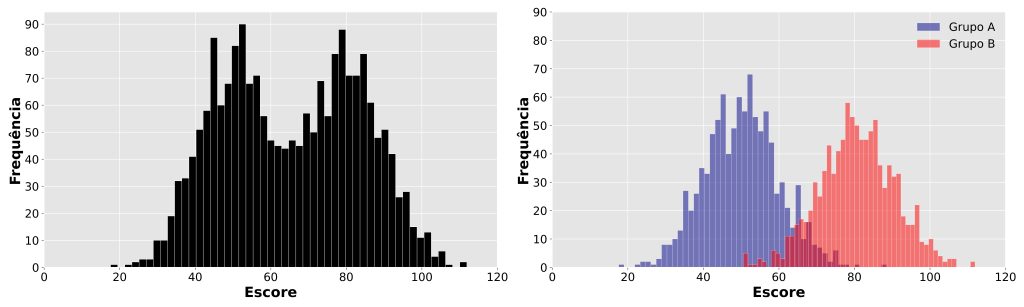
Assim como os diagramas de dispersão, também podemos dividir os histogramas por grupo (o que pode ser útil, por exemplo, quando o objetivo é comparar parâmetros entre distribuições). No exemplo da Figura 6, a distribuição à esquerda parece ser bimodal.
No entanto, quando plotamos esses mesmos dados separadamente por dois grupos, nota-se que a bimodalidade da distribuição é um artefato de duas distribuições com médias bem diferentes (o Grupo B possui média maior que Grupo A). Por exemplo, a Figura 6, painel direito, pode contribuir para entender os resultados de um teste t para grupos independentes.
Boxplots
Assim como o histograma, os boxplots (também conhecidos como diagramas de caixas, ou diagramas de caixas e bigodes) são ideais para representar a distribuição de um conjunto de dados contínuo e identificar dados extremos.
Um boxplot consiste em uma caixa que representa o intervalo interquartil (de Q1 até Q3), uma linha vertical que representa a mediana (Q2) e, finalmente, “bigodes” que se estendem para fora da caixa para mostrar os valores limítrofes que não são considerados estatisticamente extremos. Em geral, os limites dos bigodes são definidos como Q1 – 1,5 × (Q3 – Q1) e Q3 + 1,5 × (Q3 – Q1).
Podemos utilizar um boxplot para representar os escores de uma variável contínua (Figura 7, painel esquerdo), bem como para representar esses mesmos escores em função de uma variável de agrupamento (Figura 7, painel direito).

Conclusão
Neste post, discutimos a importância de escolher o gráfico adequado para diferentes tipos de dados. A escolha correta ajuda a destacar tendências, padrões e anomalias nos dados e, assim, beneficia a tomada de decisões.
Uma opção interessante para criar gráficos elegantes, personalizados e de alta qualidade é por meio do ggplot2, um pacote do R especializado nessa tarefa. Caso você ainda não seja usuário do R, então veja a novidade que preparamos a seguir!
É com grande satisfação que a Psicometria Online anuncia o curso R para Iniciantes. O curso tem como objetivo abordar todos os tópicos essenciais do R, permitindo que você explore assuntos específicos sem ser prejudicado por dúvidas básicas. Se você trabalha com pesquisa científica e deseja aprender a utilizar o R, então o curso R para Iniciantes é para você.

Precisa aprender análise de dados? Então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Como citar este post
Lima, M. (2023, 3 de maio). Como escolher o gráfico certo para seus dados? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/como-escolher-o-grafico-certo-para-seus-dados/













