Neste post, vamos introduzir o cálculo de tamanho amostral para pesquisas científicas. Mais especificamente, apresentaremos o software G*Power, uma ferramenta gratuita que facilita essa tarefa. Além disso, para ilustrar a utilidade do G*Power, descreveremos três exemplos práticos de cálculo de tamanho amostral. Por fim, vamos recomendar materiais adicionais e discutir algumas limitações do G*Power.
O que é cálculo de tamanho amostral?
O cálculo do tamanho amostral consiste em determinar quantas observações ou participantes são necessários para um estudo. Em geral, o objetivo é garantir que a amostra seja suficientemente grande para detectar, com alguma probabilidade, um efeito real, caso ele exista. A essa probabilidade, chamamos poder estatístico.
Em resumo, o poder estatístico de um estudo depende de três fatores: (a) nível de significância estatística (α); (b) tamanho da amostra (N); e (c) tamanho de efeito populacional. Da mesma forma, se soubermos o poder estatístico e o nível de significância desejados, além do tamanho do efeito que queremos detectar, podemos calcular o tamanho amostral mínimo necessário para atingir esses requisitos.
Por exemplo, se mantivermos os demais fatores constantes, ao aumentar o nível de significância de 0,05 para 0,10, o tamanho amostral mínimo necessário para detectar um efeito diminuirá. No entanto, isso aumenta a probabilidade de cometer um erro Tipo I, ou seja, rejeitar uma hipótese nula verdadeira.
Por outro lado, se aumentarmos o poder estatístico de 0,80 para 0,90, o tamanho amostral necessário também aumentará. Isso porque queremos reduzir a chance de não detectar um efeito real, ou seja, diminuir a probabilidade de cometer um erro Tipo II.

Por que o cálculo de tamanho amostral é importante?
Suponha que estamos comparando grupos experimental e controle em uma determinada variável dependente de interesse, e não observamos diferenças significativas entre os grupos. No entanto, o poder estatístico do experimento era de apenas 0,50.
Nesse caso, mesmo que o efeito de interesse exista, o delineamento teria apenas 50% de probabilidade de detectá-lo. Em outras palavras, subestimamos o tamanho amostral no planejamento da pesquisa, assumindo um elevado risco de não identificar resultados importantes (ou seja, falta de poder estatístico).
Por outro lado, imagine que coletamos dados de 200 pacientes e detectamos um efeito. No entanto, o tamanho de efeito real era grande (d = 1), o que significa que poderíamos ter alcançado um poder adequado (0,90) com apenas 46 participantes. Se os procedimentos dessa pesquisa incluírem desconforto ou alto custo, isso implica que o mau planejamento resultou em desperdício de recursos, como o tempo dos participantes e o dinheiro das agências de fomento.
Assim, o cálculo amostral adequado é uma etapa fundamental na fase de planejamento de pesquisas científicas.
O que é o G*Power?
O G*Power (Figura 1) é um software gratuito, disponível para Windows e Mac OS, usado para calcular o tamanho amostral em diferentes testes estatísticos. Com uma interface amigável, ele suporta uma ampla variedade de análises, como testes t, análises de variância, correlações e regressões, sendo amplamente utilizado em áreas como ciências sociais, comportamentais e biomédicas.
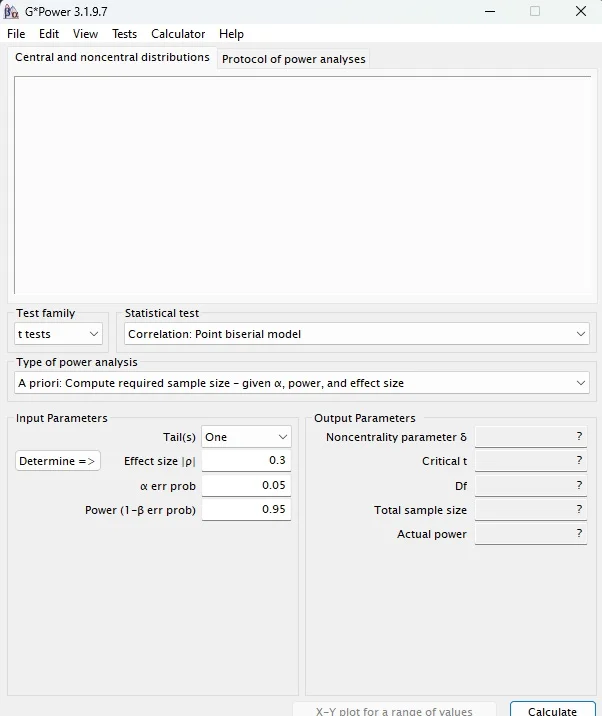
O G*Power realiza cinco tipos principais de análise de poder:
- Análise a priori: calcula o tamanho amostral mínimo necessário para detectar um efeito, com base nos níveis de significância e poder desejados;
- Análise de compromisso: calcula a relação entre erros Tipo I (α) e Tipo II (β), com base na razão β/α, no tamanho amostral e no tamanho de efeito populacional;
- Análise de critério: calcula o nível de significância necessário, dado o poder, o tamanho da amostra e o tamanho de efeito esperado;
- Análise post hoc: estima o poder de um estudo após a coleta de dados, com base na amostra e nos níveis de significância e tamanho de efeito;
- Análise de sensibilidade: determina o menor efeito que pode ser detectado, considerando o poder, o nível de significância e a amostra definidos.
Entre essas, a análise a priori é a que usamos para o cálculo de tamanho amostral. O G*Power oferece saídas numéricas e gráficas, facilitando o planejamento de estudos.
Em seguida, veremos exemplos práticos de como usar o G*Power. Para baixar o software, acesse o site da Universität Düsseldorf (https://www.psychologie.hhu.de/arbeitsgruppen/allgemeine-psychologie-und-arbeitspsychologie/gpower).
Cálculo de tamanho amostral no G*Power
Exemplo 1: diferenças entre médias pareadas no G*Power
Vamos replicar um protocolo de indução de humor triste. O humor de cada participante será avaliado antes e após a indução. O estudo original apresentou apenas estatísticas descritivas de humor triste pré- (M = 25,12, DP = 5,63) e pós-indução (M = 21,73, DP = 5,66), mas sem o tamanho de efeito.
Primeiramente, selecionaremos as seguintes opções no G*Power:
- Test family: t tests;
- Statistical test: Means: Difference between two dependent means (matched pairs), isto é, teste t para grupos pareados;
- Type of power analysis: A priori, ou seja, cálculo de tamanho amostral.
Como o tamanho de efeito não foi reportado, clicaremos em Determine para calcular o d de Cohen, inserindo os dados do estudo original. No entanto, o cálculo de d de Cohen exige o coeficiente de correlação entre medidas pareadas, que não foi informado. Nesse caso, definiremos o valor como 0,5 (Figura 2). Em situações reais, contudo, seria importante testar o impacto de diferentes valores de r no cálculo de tamanho amostral.
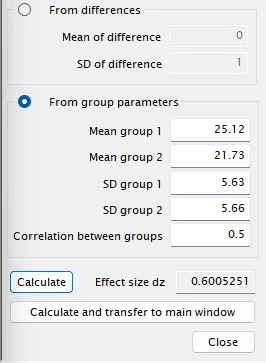
Após clicar em Calculate and transfer to main window, definiremos o teste como bicaudal (Tail(s) = Two), o nível de significância como 0,05 e o poder como 0,80. Em seguida, clicaremos em Calculate.
A Figura 3 apresenta o resultado, indicando que são necessários pelo menos 24 participantes para atingir um poder de 80% para detectar um tamanho de efeito de d = 0,60, com um nível de significância de 0,05.
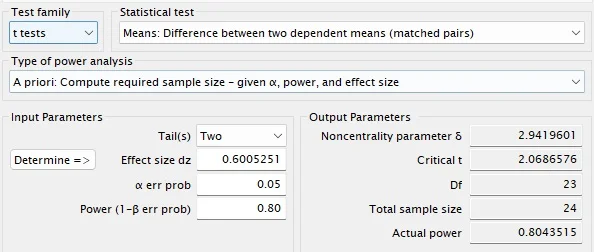
Exemplo 2: correlação bivariada no G*Power
Suponha que queremos correlacionar as atitudes de pós-graduandos em relação à matemática com suas notas finais na disciplina Métodos Inferenciais. Nosso objetivo é detectar uma correlação de pelo menos r = 0,30 (teste bicaudal), com nível de significância de 0,05 e poder de 0,95.
Na Figura 4, os parâmetros de entrada estão à esquerda, conforme descrito. À direita, temos os resultados da análise de poder a priori.
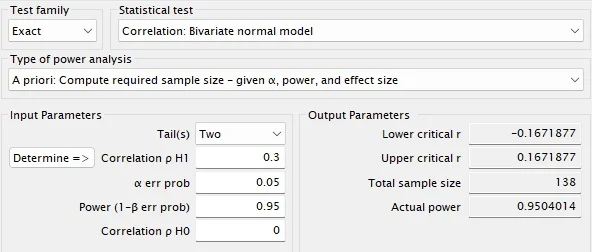
Como mostrado na Figura 4, precisaremos de pelo menos 138 participantes para detectar uma correlação de r = 0,30 entre atitudes e notas, com 95% de poder e significância de 0,05.
Entretanto, o poder estatístico é relativo: se o tamanho do efeito aumentar, o poder também aumenta, e vice-versa. Desse modo, podemos nos questionar: qual seria o tamanho amostral necessário se a correlação e o poder almejado fossem distintos dos valores usados na Figura 4?
A Figura 5 ilustra o tamanho amostral necessário para três valores de r (0,25, 0,30 e 0,35) e diferentes níveis de poder (de 0,50 a 0,95, em incrementos de 0,05).
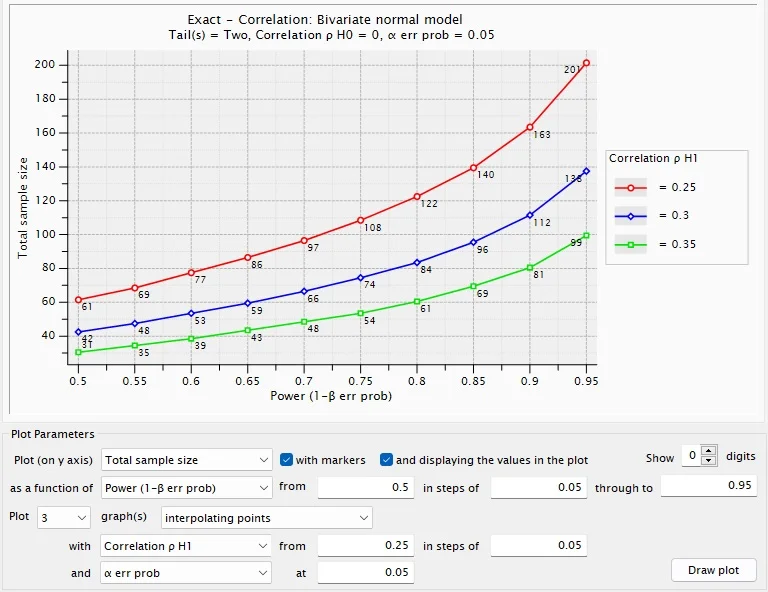
A Figura 5 indica que, com efeito menor (linha vermelha), o tamanho amostral deve ser maior. Por exemplo, se a correlação for r = 0,25, a amostra original, estimada em 138 participantes, terá pouco menos de 0,85 de poder (140 participantes = 0,85 de poder). Isso demonstra como o G*Power facilita a visualização da relação entre tamanho amostral, tamanho de efeito e poder estatístico, sendo uma ferramenta útil para planejar estudos com maior precisão.
Exemplo 3: efeito de interação na ANOVA no G*Power
Vamos investigar o efeito de uma intervenção de reabilitação cognitiva (experimental, controle) sobre a memória em quatro grupos etários (50, 60, 70, 80 anos). Esse delineamento pode ser analisado por análise de variância 2 × 4.
Nosso objetivo é detectar um efeito de interação Grupo Etário × Intervenção de eta ao quadrado parcial (η²p) = 0,06, com poder de 0,90 e nível de significância de 0,05.
Primeiramente, selecionaremos as seguintes opções no G*Power:
- Test family: F tests;
- Statistical test: ANOVA: Fixed effects, special, main effects and interactions;
- Type of power analysis: A priori, ou seja, cálculo de tamanho amostral.
Como o G*Power usa f de Cohen como medida de efeito, precisamos converter o η²p para f de Cohen. Para isso, clicamos em Determine e, na nova janela, inserimos o η²p para calcular o f (Figura 6).
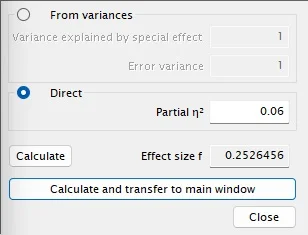
Em seguida, clicamos em Calculate and transfer to main window. Depois, inserimos o valor do nível de significância (0,05), do poder (0,90), do numerator df (gl = 4 – 1 = 3) e do number of groups (4). Por fim, clicamos em Calculate.
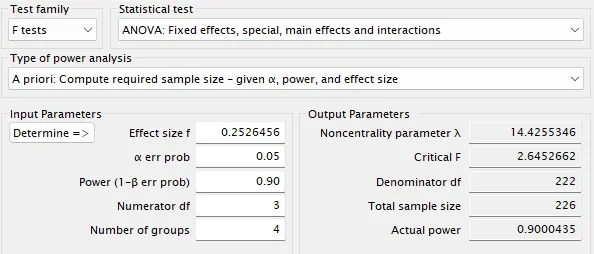
A Figura 7 mostra que, para detectar um η²p = 0,06 com 90% de poder e significância de 0,05, precisamos de pelo menos 226 participantes. Desse modo, se quisermos o mesmo número de participantes por grupo, serão necessários 29 participantes por célula, resultando em um total de 232 participantes (29 × 8 = 232).
Materiais adicionais e limitações do G*Power
Anteriormente, apresentamos três exemplos de cálculo de tamanho amostral no G*Power. No entanto, esses exemplos representam apenas uma pequena parte das capacidades do G*Power, que permite calcular o tamanho amostral para muitos outros testes estatísticos, tais como regressões lineares, logísticas e de Poisson.
Para uma lista completa de possibilidades, o leitor interessado deve consultar Faul et al. (2007, 2009), além de acessar o manual do G*Power 3.1.
No entanto, apesar de sua ampla utilidade, o G*Power também apresenta algumas limitações. Por exemplo, ele não realiza cálculos de tamanho amostral para estudos focados em variáveis latentes, como em análises fatoriais ou modelagem por equações estruturais. Além disso, o G*Power não oferece suporte para estudos que utilizam a teoria de resposta ao item ou que aplicam modelos lineares mistos.
Conclusão
Neste post, apresentamos o G*Power, um software gratuito usado para calcular o tamanho amostral em diferentes tipos de testes estatísticos. Além disso, por meio de exemplos práticos, ilustramos como calcular o tamanho amostral no G*Power. Se você gostou desse conteúdo, aproveite e também se inscreva em nosso canal do YouTube!
Se você quer aprender sobre esse e outros conteúdos, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Faul, F., Erdfelder, E., Lang, A.-G., & Buchner, A. (2007). G*Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behavior Research Methods, 39, 175–191. https://doi.org/10.3758/BF03193146
Faul, F., Erdfelder, E., Buchner, A., & Lang, A.-G. (2009). Statistical power analyses using G*Power 3.1: Tests for correlation and regression analyses. Behavior Research Methods, 41, 1149–1160. https://doi.org/10.3758/BRM.41.4.1149
Como citar este post
Lima, M. (2024, 30 de outubro). Como fazer o cálculo de tamanho amostral no G*Power? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/como-fazer-o-calculo-de-tamanho-amostral-no-gpower/













