Se você já fez um curso de metodologia científica, é possível que você já tenha ouvido a expressão “correlação não implica causalidade”. Isto é, identificar uma correlação é uma condição necessária, mas não suficiente, para inferirmos causalidade.
No post de hoje, abordaremos de maneira intuitiva por que correlação não implica causalidade. Nele apresentaremos dois problemas comuns em estudos correlacionais que impedem inferências causais.
O que é correlação?
Imagine dois dançarinos no palco, cada um representando metaforicamente uma variável. A correlação é como uma música que descreve como esses dançarinos se movem juntos. Ela é uma medida da força e da direção do relacionamento linear entre duas variáveis.

Se você já usou o SPSS ou qualquer outro programa estatístico, você provavelmente sabe que a relação entre duas variáveis pode ser quantificada por um coeficiente chamado coeficiente de correlação de Pearson, representado pela letra r. Em síntese, esse coeficiente varia de –1 a +1, onde:
- r = +1: nosso par dança em perfeita sincronia! Se um avança, então o outro também avança. Estamos diante de uma correlação positiva perfeita;
- r = –1: os dançarinos estão executando uma dança espelhada. Quando um avança, o outro recua. Essa é uma correlação negativa perfeita;
- r = 0: os dançarinos estão em seus próprios mundos, cada um se movendo de maneira descoordenada e sem sincronia com os movimentos do seu par. Tal cenário indica uma ausência de correlação.

Por que correlação não implica causalidade?
Quando dizemos que duas variáveis estão correlacionadas, estamos afirmando que existe um padrão nos dados. Entretanto, é importante ressaltar que não somos capazes de determinar qual variável exerce influência sobre a outra apenas com base na correlação.
Retomando a metáfora dos dançarinos, os movimentos sincronizados deles não nos permitiriam afirmar que um dançarino está causando o movimento do outro. Desse modo, tudo o que poderíamos concluir é que eles se movem juntos de uma maneira previsível.
Em seguida, descreveremos os dois problemas de se inferir causalidade a partir de correlação.
O problema da direcionalidade
O problema da direcionalidade consiste no fato de que, embora possamos saber que duas variáveis estão correlacionadas, a correlação sozinha é insuficiente para que saibamos a direção da relação entre variáveis.
Por exemplo, uma pesquisa identificou uma correlação negativa entre engajamento em atividade física e níveis de ansiedade: quem tem escore mais alto de ansiedade tende a ter menos tempo de engajamento em atividade física, e vice-versa. No entanto, a Figura 1 mostra que podemos hipotetizar mecanismos direcionais distintos para explicar essa correlação.

Considere um segundo exemplo. Em outra pesquisa, observou-se uma correlação positiva entre níveis de sociabilidade e de satisfação com a vida, isto é, pessoas com maiores tendências em se engajar em relações interpessoais reportam níveis mais elevados de satisfação com a vida. Todavia, a Figura 2 sugere que não é simples determinar qual é a direção da relação entre essas variáveis.

Note que, nos parágrafos anteriores, destacamos em negrito as descrições em termos puramente correlacionais. Nesses trechos, não foram feitas afirmações sobre qual variável exerce um efeito causal sobre a outra. Recomendamos que você tenha em mente esse mesmo cuidado em seus estudos, ou seja, que avalie se suas escolhas metodológicas e analíticas justificam inferências causais com base nos resultados obtidos.
O problema da terceira variável
Há situações em que duas variáveis podem parecer “dançar juntas”, mas, na realidade, é uma terceira variável que está influenciando ambas e “conduzindo a dança”. Essa terceira variável é chamada de variável confundidora, e esse cenário, por sua vez, como o problema da terceira variável.
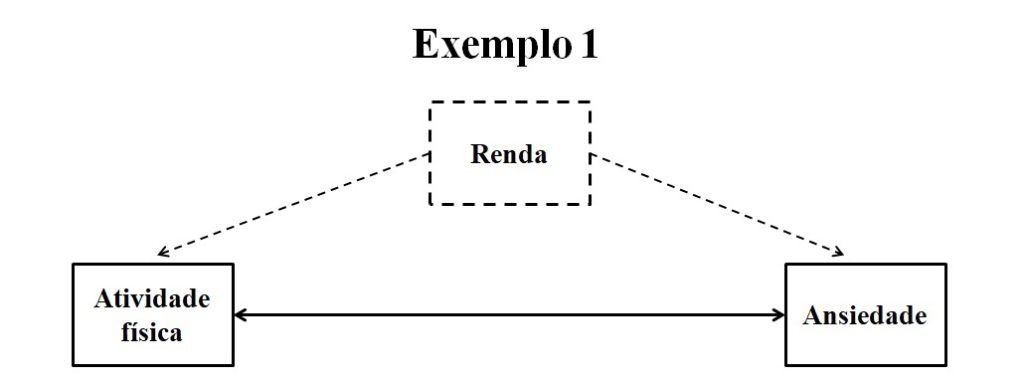
Na Figura 3, uma possível variável confundidora é a renda: pessoas com renda mais elevada têm uma condição de vida que as permite se engajar em mais atividades físicas e que também as leva a ter níveis reduzidos de ansiedade.
Se isso for verdade, então temos evidências de uma correlação espúria, isto é, uma relação estatística enganosa, que pode ser totalmente explicada em termos de uma terceira variável.
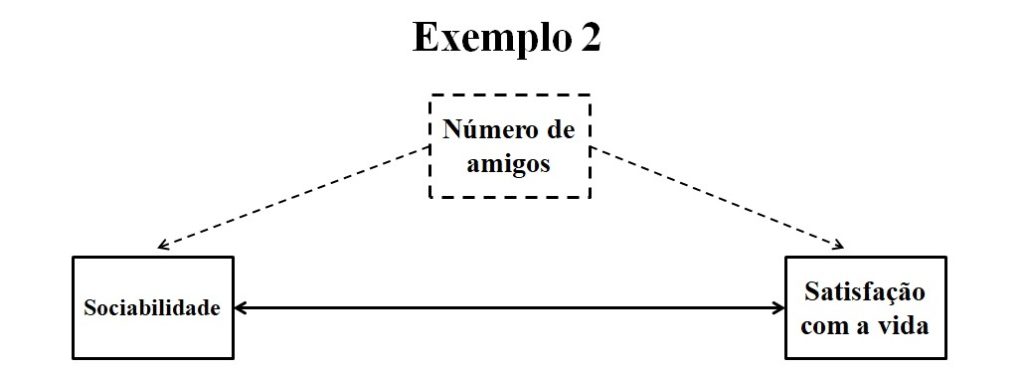
Por outro lado, na Figura 4, a variável confundidora poderia ser o número de amigos: ter mais amigos pode levar as pessoas a serem mais sociáveis e a terem níveis mais elevados de satisfação com a vida.
Se esse realmente for o caso, então o relacionamento entre sociabilidade e satisfação com a vida também pode ser classificado como uma correlação espúria.
A mensagem principal das duas últimas seções é que, embora identificar correlações entre variáveis tenha relevância teórica e prática, devemos estar cientes que os problemas da direcionalidade e da terceira variável nos impede de tomar a correlação como condição suficiente para inferirmos causalidade.
Veja também:
Outros exemplos de correlações espúrias
Correlação entre o consumo de sorvetes e o número de afogamentos
Em muitos lugares, as vendas de sorvete e os afogamentos estão altamente correlacionados. Mas será que isso significa que comprar sorvete causa afogamentos? Ou, por outro lado, que se afogar causa um desejo repentino de consumir sorvetes?

Claro que não! Ambas as variáveis são influenciadas por uma terceira variável, a saber, a temperatura. Em dias quentes, as pessoas tendem a comprar mais sorvetes e também a frequentar mais a praia, aumentando assim o número de banhistas e, por conseguinte, o risco de afogamentos.
Correlação entre o número de piratas e o aquecimento global
Algumas pessoas brincam que o número de piratas no mundo está negativamente correlacionado com o aumento das temperaturas globais. Em outras palavras, quanto mais piratas, menos aquecimento global teríamos.

Com base nesse exemplo, o que podemos concluir? Que menos piratas causam o aquecimento global? Ou talvez que governantes devem investir na regulamentação da profissão de pirata como forma de combater o aquecimento global? Seria divertido pensar assim, mas, obviamente, essa é uma correlação espúria.
Correlação entre a popularidade de um meme e o consumo de queijo
O site Spurious Correlations compila uma série de correlações bem-humoradas, mas sem sentido teórico. Por exemplo, o site relata a correlação entre a popularidade do meme “this is fine” e o consumo de queijo por parte de norte-americanos. Em outras palavras, em anos em que a popularidade do meme esteve maior, houve uma tendência a maiores níveis de consumos de queijo, r = 0,93, p < 0,01.

Qual é a explicação para uma correlação assim tão forte? Ao invés de hipotetizar explicações mirabolantes, vamos a uma mais simples: correlação espúria. Se você sair correlacionando milhares de pares variáveis entre si, eventualmente emergirão algumas correlações elevadas e surpreendentes, mas sem qualquer necessidade de explicação teórica.
Recomendamos que você visite o site Spurious Correlations para conhecer outras correlações espúrias bizarras que, definitivamente, nos alertam sobre os riscos de interpretar correlação como indicativo de relações causais.
Conclusão
Neste post, explicamos por que correlação não implica causalidade. Apesar de a correlação ser uma técnica poderosa na caixa de ferramentas de pesquisadores, seus resultados devem ser interpretados com cautela.
Um coeficiente de correlação pode apontar para possíveis relações que devem ser exploradas em estudos futuros. Entretanto, não podemos saltar diretamente para conclusões causais com base apenas no coeficiente de correlação.
Então, da próxima vez que você ouvir alguém dizer, “Ah, mas isso e aquilo estão correlacionados!”, você pode sorrir sabiamente e responder: “Sim, mas correlação não implica causalidade!”.
Esperamos que este post tenha ajudado você a entender melhor o conceito de correlação. Aproveite e se inscreva em nosso canal do YouTube para aprimorar suas habilidades em análise de dados!
Gostou desse conteúdo? Precisa aprender análise de dados? Então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Shaughnessy, J. J., Zechmeister, E. B., & Zechmeister, J. S. (2012). The scientific method. In J. J. Shaughnessy, E. B. Zechmeister, & J. S. Zechmeister, Research methods in psychology (9th ed., pp. 27–56). McGraw-Hill.
Como citar este post
Lima, M. (2023, 10 de setembro). Correlação não implica causalidade. Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/correlacao-nao-implica-causalidade/













