Neste post, vamos explorar duas medidas de tamanho de efeito para o teste qui-quadrado de independência: o coeficiente phi e o V de Cramér.
Introdução
Em muitas situações, pesquisadores investigam a associação entre duas variáveis categóricas. Por exemplo, pode-se investigar se há associação entre coorte geracional (geração X, Y, Z) e rede social preferida (Instagram, Facebook, TikTok, Twitter).
No exemplo anterior, as variáveis permitem apenas operações de contagem (frequência absoluta e percentual, moda), necessitando assim de técnicas estatísticas adequadas para suas análises. Uma boa escolha é o qui-quadrado de independência, acompanhado de medidas de tamanho de efeito para testes de associação.

O que é o teste qui-quadrado de independência?
O teste qui-quadrado de independência é uma técnica estatística que compara as frequências observadas de casos que ocorrem em cada uma das categorias com as frequências que seriam esperadas se não houvesse associação entre as duas variáveis.
Esse teste calcula uma estatística, denominada de χ2 (χ é a letra grega chi), que é comparada com uma distribuição de χ2, cujos valores variam de zero a infinito. Se o valor de χ2 em nossa amostra for mais extremo que um valor crítico de referência dessa distribuição, então rejeitamos a hipótese nula de não associação entre variáveis.
O teste qui-quadrado, quando estatisticamente significativo, permite a conclusão de que há associação entre variáveis. Por exemplo, se estivermos comparando coorte geracional e preferência por redes sociais, nossa conclusão seria de que essas duas variáveis estão associadas, isto é, diferentes coortes geracionais preferem redes sociais distintas.
Mas qual é o tamanho dessa associação? Infelizmente, essa informação não é fornecida pela estatística χ2. Sendo assim, para estimarmos o tamanho da associação, precisamos recorrer a medidas de tamanho de efeito.
O que são medidas de tamanho de efeito?
Enquanto o teste de significância da hipótese nula tradicionalmente enfatiza uma decisão dicotômica entre rejeitar ou não rejeitar a hipótese nula, medidas de tamanho de efeito permitem uma apreciação dos resultados em termos de “níveis de falsidade da hipótese nula”.
Sendo assim, o conceito de tamanho de efeito está relacionado à ideia de importância prática dos resultados (Kelley & Preacher, 2012). Em síntese, no contexto do teste qui-quadrado de independência, medidas de associação forneceriam uma síntese numérica da força da associação entre variáveis.
No exemplo das redes sociais, uma associação forte indicaria que saber a idade de uma pessoa seria altamente preditivo de qual rede social ela prefere, enquanto uma associação fraca sugeriria que nossa predição não é assim tão confiável.
Em seguida, explicaremos duas medidas de associação para o teste qui-quadrado de independência.
Coeficiente phi
O que é o coeficiente phi?
O coeficiente φ (a letra grega phi) é uma medida de associação entre duas variáveis binárias. No entanto, para o coeficiente phi ser uma medida viável, é necessário que ambas as variáveis de interesse tenham apenas duas categorias (p.ex., doente/não doente, vivo/morto, cachorro/gato).
Note que a variável não precisa genuinamente ter apenas dois níveis no mundo real. Por exemplo, sabemos que animais podem ser classificados em outras categorias além de cães e gatos. O importante para o cálculo do coeficiente é que, na amostra, o pesquisador tenha codificado a variável como tendo apenas dois níveis.
Como calcular o coeficiente phi?
Eis um exemplo: pesquisadores recrutam uma coorte de participantes nascidos entre 1965 e 1980 (geração X), e outra de participantes nascidos entre 1997 e 2012 (geração Z). Em seguida, pesquisadores solicitam que os participantes respondam à seguinte pergunta: qual é sua rede social preferida?
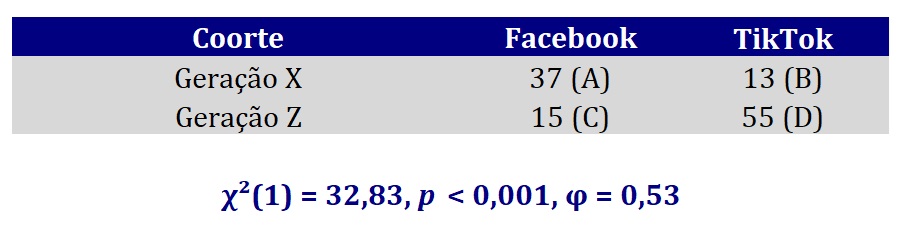
A Figura 1 apresenta uma tabela de contingências 2 × 2 com os resultados dessa pesquisa. Por exemplo, a célula A indica que 37 participantes da geração X preferem o Facebook, enquanto a célula D indica que 55 participantes da geração Z preferem o TikTok.
O coeficiente phi é calculado da seguinte forma:
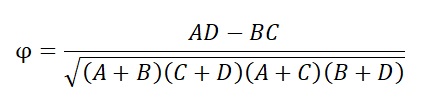
onde A, B, C e D se referem às quatro células da Figura 1. Aplicado aos dados da Figura 1, temos:
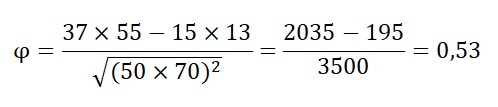
Desse modo, φ = 0,53, indicando uma associação entre coorte e preferência por rede social: há uma preferência pelo Facebook por parte de participantes da geração X, e pelo TikTok por parte de participantes da geração Z.
Se todas as observações da amostra estiverem concentradas na diagonal principal (células A e D), então o valor do numerador será idêntico ao do denominador. Desse modo, φ = 1, indicando associação perfeita entre as variáveis.
Por outro lado, se o produto das células da diagonal principal for igual ao produto dos elementos da diagonal secundária (AD = BC), o numerador resultará em zero e, por conseguinte, φ = 0.
Sendo assim, concluímos que a fórmula do coeficiente phi calcula em que medida as células da diagonal principal são mais (ou menos) populosas que as células da diagonal secundária.
Como interpretar o sinal do coeficiente phi?
Como a rede social é uma variável nominal, poderíamos inverter a ordem de apresentação das colunas. Embora isso não impacte o denominador da fórmula do coeficiente , tal inversão afeta o numerador: os valores calculados nos dois termos de AD – BC trocam de posição com a inversão das colunas. Sendo assim, essa inversão teria um efeito sobre o sinal do coeficiente phi.
As Figuras 3 e 4 ilustram essa ideia: o sinal do coeficiente phi, portanto, indica apenas se as células da diagonal principal (Figura 3) ou da diagonal secundária (Figura 4) são as mais frequentes.


Como calcular o coeficiente phi com base no teste qui-quadrado?
Na penúltima seção, apresentamos a fórmula do coeficiente phi com base na tabela de contingências 2 × 2. Uma forma ainda mais simples de calculá-lo é com base na estatística do teste qui-quadrado:
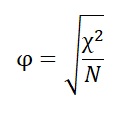
onde N é o total de observações na amostra. Com base nessa fórmula, teríamos:
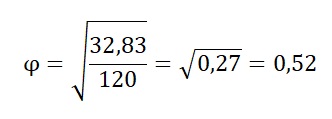
O que leva a resultados similares aos reportados anteriormente, exceto por pequenas diferenças de arredondamento. Além disso, vale ressaltar que, nessa fórmula alternativa, o valor do coeficiente será sempre positivo.
V de Cramér
O que é o V de Cramér?
O V de Cramér é uma generalização do coeficiente phi, isto é, ele também expressa a força da associação entre duas variáveis nominais. No entanto, diferente do coeficiente phi, o V de Cramér também se aplica a variáveis politômicas (p.ex., onívoro/vegetariano/vegano, autoritário/democrático/laissez-faire, Instagram/Facebook/TikTok/Twitter).
Como calcular o V de Cramér?
O V de Cramér é calculado a partir da estatística do teste qui-quadrado:
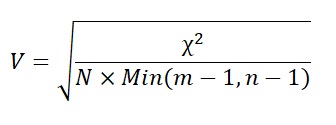
onde m e n representam o número de linhas e o número de colunas, respectivamente, da tabela de contingências. Desse modo, em uma tabela de contingências 2 × 2, o denominador da fórmula se reduz a N, fazendo com que o coeficiente phi e V produzam resultados idênticos.
Para ilustrar o cálculo do V de Cramér, modificaremos o exemplo anterior, acrescentando 20 participantes da geração X e 10 da geração Z à amostra original. Esses novos participantes preferem o Instagram como rede social. As demais células são idênticas as do exemplo anterior, conforme mostra a Figura 5.

Aplicando a fórmula do V de Cramér, temos:
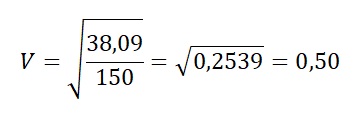
Esse resultado indica uma associação grande entre coorte e preferência por rede social. Contudo, o valor diminuiu um pouco em relação ao exemplo anterior por conta da inclusão de participantes que preferem o Instagram, que diminuiu a preferência relativa em cada coorte por uma determinada categoria modal (i.e., Facebook para a geração X; TikTok para a geração Z).
Quando usar o coeficiente phi e o V de Cramér?
Você pode usar tanto o coeficiente phi quanto o V de Cramér para medir a força da associação entre duas variáveis categóricas. Todavia, a escolha entre phi e V depende do número de categorias que cada uma das variáveis possui.
Use o coeficiente phi apenas quando sua análise se basear em tabelas de contingências 2 × 2. Por outro lado, use o V de Cramér quando você tiver mais de duas categorias para uma ou ambas as variáveis.
Como interpretar os valores do coeficiente phi e do V de Cramér?
Para a tabela de contingências 2 × 2, o coeficiente phi pode ser interpretado da seguinte maneira (Kotrlik et al., 2011):
- 0 ≤ φ < 0,10: irrisório;
- 0,10 ≤ φ < 0,20: fraco;
- 0,20 ≤ φ < 0,40: moderado;
- 0,40 ≤ φ < 0,60: relativamente forte;
- 0,60 ≤ φ < 0,80: forte;
- 0,80 ≤ φ < 1: muito forte;
- φ = 1: perfeito.
A interpretação é análoga quando consideramos valores negativos.
Por outro lado para interpretar o V de Cramér, também precisamos considerar os graus de liberdade do teste qui-quadrado de independência correspondente. Assim, uma sugestão é apresentada na Figura 6 (Cohen, 1988).
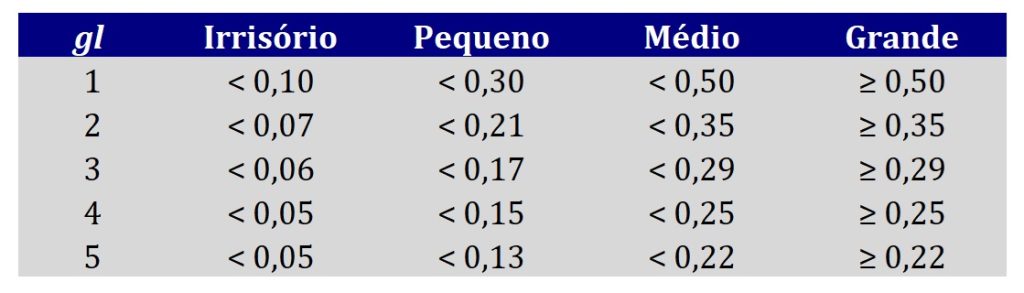
Ressaltamos, contudo, que essas orientações não são de caráter prescritivo. Desse modo, é importante que a força da associação seja considerada à luz da sua área de pesquisa.
Conclusão
Neste post, apresentamos duas medidas de associação para o teste qui-quadrado de independência, a saber, o coeficiente phi e o V de Cramér. Se você quiser saber mais sobre o teste qui-quadrado de independência, então recomendamos que leia nosso post sobre o tema.
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed). Lawrence Erlbaum Associates, Publishers.
Kelley, K., & Preacher, K. J. (2012). On effect size. Psychological Methods, 17(2), 137–152. https://doi.org/10.1037/a0028086
Kotrlik, J. W., Williams, H. A., & Jabor, M. K. (2011). Reporting and interpreting effect size in quantitative agricultural education research. Journal of Agricultural Education, 52(1), 132–142. https://doi.org/10.5032/jae.2011.01132
Howell, D. C. (2013). Alternative correlational techniques. In D. C. Howell, Statistical methods for psychology (8th ed., pp. 303–324). Wadsworth Cengage Learning.
Como citar este post
Lima, M. (2023, 7 de agosto). Medidas de associação: Coeficiente phi e V de Cramér. Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/medidas-de-associacao-coeficiente-phi-e-v-de-cramer/













