A correlação de Pearson é uma técnica estatística para medir se duas variáveis estão linearmente relacionadas. Essa técnica também pode ser chamada de r de Pearson, correlação produto–momento de Pearson ou, mais coloquialmente, de correlação de Pearson.
Neste post, você aprenderá o que significa duas variáveis estarem linearmente relacionadas. Além disso, você aprenderá o que é e como interpretar o coeficiente r de Pearson e o coeficiente de determinação. Por fim, discutiremos sobre a significância estatística, sobre o cálculo de intervalos de confiança e em quais situações você não deve usar o r de Pearson.
Veja também:
O que é relação linear entre variáveis?
Para ilustrar a ideia de relação linear entre variáveis, forneceremos algumas intuições gráficas a seguir.
Correlação positiva
No diagrama de dispersão da Figura 1, o eixo x representa uma variável, enquanto o eixo y representa outra variável qualquer. Além disso, cada ponto representa os escores observados de um participante nas duas variáveis.
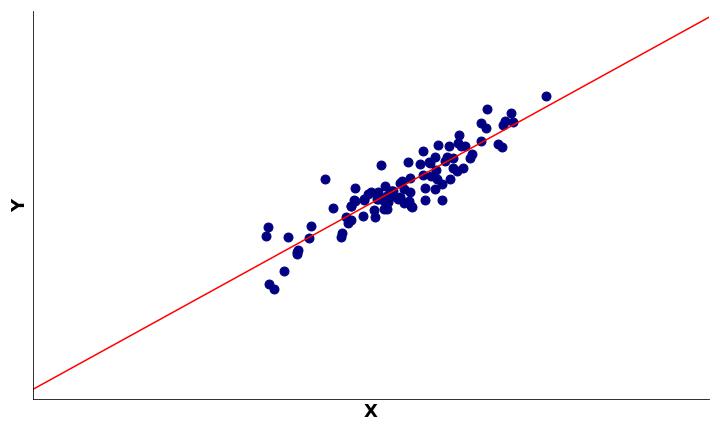
Na Figura 1, as observações estão próximas à linha vermelha, que representa a linha de tendência dos dados. À medida que os valores aumentam em um eixo, eles também aumentam no outro eixo. Em outras palavras, a Figura 1 mostra duas variáveis que estão positivamente correlacionadas.

Correlação negativa
A Figura 2 mostra o padrão diametralmente oposto.
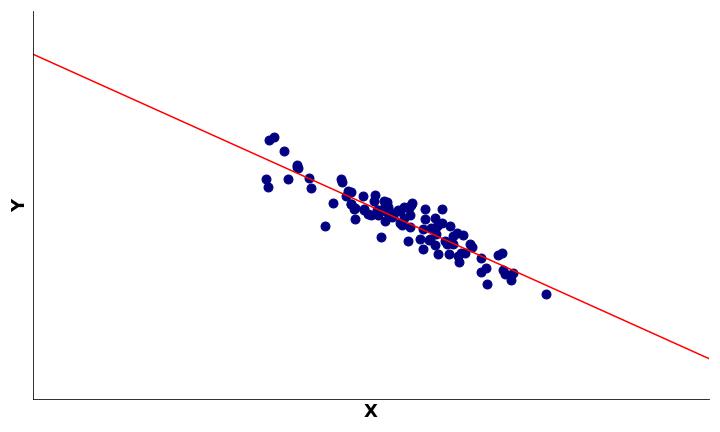
Na Figura 2, as observações também estão próximas à linha de tendência dos dados. No entanto, note que agora essa linha tem inclinação descendente. Isto é, à medida que os valores aumentam em um eixo, eles tendem a diminuir no outro eixo. Em outras palavras, a Figura 2 mostra duas variáveis que estão negativamente correlacionadas.
Correlação nula
Agora, contraste os cenários anteriores com o que vemos na Figura 3.
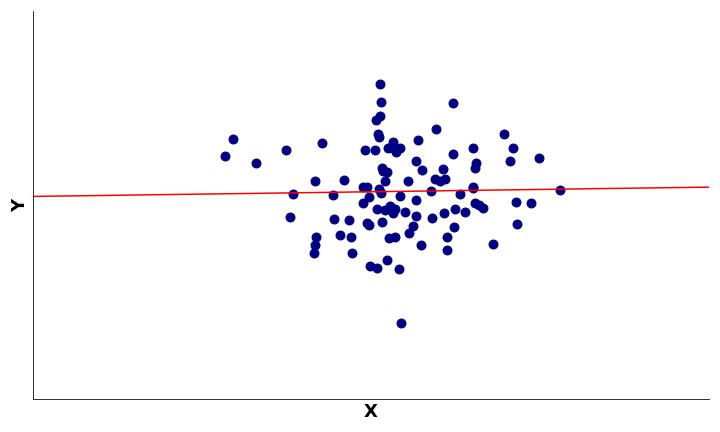
Como podemos ver na Figura 3, a linha vermelha está aproximadamente paralela à reta do eixo x, ou seja, temos a ausência de tendência linear entre variáveis. Em outras palavras, A Figura 3 mostra um exemplo de duas variáveis que têm uma correlação nula.
Pontos importantes sobre as relações lineares
Com isso em mente, eis alguns pontos importantes que devem ser lembrados sobre as relações lineares:
- A mudança em uma variável está associada à mudança na outra variável (Figuras 1 e 2);
- Tal mudança é sempre constante, ou seja, não importa se uma variável aumenta de 1 para 2 ou de 50 para 51, pois sempre que aumentarmos uma unidade no valor da primeira variável, esperaremos que o valor aumentado na outra será o mesmo.
O que significam os resultados da correlação de Pearson?
O r de Pearson é uma métrica que expressa a relação linear entre variáveis por meio de um número que vai de –1 a +1. Isto é, quanto mais próximo dos extremos (–1 ou +1), maior é a força da correlação. Por outro lado, valores próximos de zero indicam que a correlação é fraca (Figura 3).
O sinal da correlação, por sua vez, indica a direção da relação entre variáveis. Se a correlação é positiva, então o aumento em uma variável implica o aumento na outra variável (Figura 1). Por outro lado, se a correlação é negativa, então o aumento em uma variável implica o decréscimo na outra variável (Figura 2).
A Figura 4 associa diferentes valores de r de Pearson a diferentes padrões de diagramas de dispersão. Quanto mais forte é a correlação entre variáveis, mais nitidamente os pontos parecem indicar um padrão gráfico linear.

Como interpretar os valores do coeficiente de correlação?
Até aqui, você já deve ter uma noção de como interpretar a direção e a força da correlação, mas pode querer uma interpretação mais objetiva do significado dos números apresentados nos testes de correlação. Contudo, não existe consenso sobre o a interpretação dos valores da correlação. O que existem, de fato, são algumas recomendações.
Cohen (1992), por exemplo, sugere os seguintes pontos de corte:
- r = |±0,10| → correlação fraca;
- r = |±0,30| → correlação moderada;
- r = |±0,50| → correlação forte.
Por outro lado, Rumsey (2023) traz a seguinte sugestão de tamanhos de efeito:
- r = |±1| → relação linear perfeita;
- r = |±0,70| → relação linear forte;
- r = |±0,50| → relação linear moderada;
- r = |±0,30| → relação linear fraca;
- r = 0 → ausência de relação linear.
Note que as interpretações são simétricas, independentemente de o coeficiente ser positivo ou negativo. Além disso, as sugestões acima não são prescritivas. Isto quer dizer, portanto, que pesquisadores devem sempre interpretar seus coeficientes à luz da literatura de suas respectivas áreas de pesquisa.
Como avaliar a correlação de Pearson através do coeficiente de determinação?
Além das recomendações acima, podemos interpretar a correlação através do coeficiente de determinação, representado por r2. Se multiplicarmos o r2 por 100, então podemos interpretar o valor obtido como o percentual de variância que uma variável explica da outra, um valor conhecido como variância explicada.
Por exemplo, se r = 0,10, então 1% da variância de uma variável pode ser explicada pela outra, pois r2 = 0,102 = 0,01. Se r = 0,30, então 9% da variância de uma variável pode ser explicada pela outra, pois r2 = 0,302 = 0,09. A Figura 5 sumariza a relação entre os valores da correlação de Pearson, r, e os valores do coeficiente de determinação, r2.
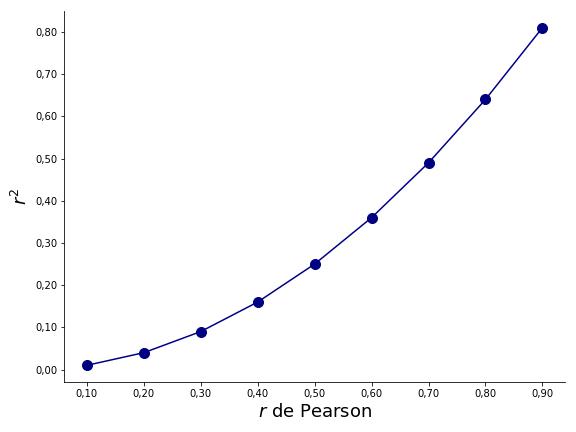
Reforçando, é importante que se tenha em mente que sugestões de interpretação são sempre arbitrárias. É possível que, em um contexto de competições esportivas de alto rendimento, um r2 = 0,09 tenha relevância prática, enquanto em um contexto de treinamento cognitivo, um r2 = 0,36 seja de pouca aplicabilidade, devido aos custos financeiros e de tempo para implementação do treinamento.
A mensagem final desta seção é que, se quisermos determinar se o tamanho de efeito é forte ou não, então precisaremos sempre olhar o contexto de pesquisa ou de aplicação no qual ele está inserido.
Qual é a importância da significância estatística para a correlação de Pearson?
Ao analisar correlações, você não deve se esquecer de que, como em qualquer estatística frequentista, é necessário olhar os valores de significância dos testes (isto é, se o valor de p é menor que o critério de significância pré-estabelecido). Em ciências humanas e sociais, é comum aceitarmos valores de correlações (e demais testes) quando p for menor do que 0,05 (isto é, alfa é definido como 0,05).
É possível ser ainda mais rigoroso utilizando técnicas de reamostragem, possibilitando informar os valores de intervalos de confiança (IC) do r. Nesse caso, nós consideraríamos que os valores de r são confiavelmente diferentes de zero quando os limites inferior e superior do IC não têm sinais diferentes. Em outras palavras, quando nosso nível de incerteza se restringe ao r de Pearson sempre com o mesmo sinal.
Por exemplo, se r = 0,30, IC 95% = [0,15, 0,45], então podemos concluir que há evidência suficiente em nossa amostra para afirmarmos que existe uma relação positiva entre as variáveis que estudamos. Em contrapartida, se r = 0,30, IC 95% = [–0,05, 0,65], então não temos evidência o suficiente para afirmarmos que nossa correlação é estatisticamente distinta de zero. Nesse último caso, temos valores positivos e negativos dentro do intervalo e, portanto, um indicativo de um valor de r não confiavelmente diferente de zero. Em postagens futuras, iremos abordar intervalos de confiança com mais detalhes.
Quando não utilizar a correlação de Pearson?
A correlação de Pearson, apesar de muito útil, não pode ser utilizada em qualquer contexto. Desse modo, você deve procurar alternativas à correlação de Pearson quando:
- A relação entre as variáveis não for linear;
- As variáveis não forem contínuas.
Se a sua análise se encaixa em um desses casos, então você deve procurar alternativas não paramétricas para testar a correlação entre variáveis. Duas delas são o τ (letra grega tau) de Kendall e o ρ (letra grega rho) de Spearman.
Conclusão
Neste post, você aprendeu o que significa duas variáveis estarem linearmente relacionadas. Além disso, você também aprendeu o que é e como interpretar o coeficiente de correlação de Pearson e o coeficiente de determinação. Por fim, descrevemos brevemente as questões da significância estatística, do cálculo de intervalos de confiança ao redor do r de Pearson, e em quais situações você não deve utilizar a correlação de Pearson.
Gostou desse conteúdo? Aproveite e também se inscreva em nosso canal do YouTube!
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Cohen, J. (1992). Statistical power analysis. Current Directions in Psychological Science, 1(3), 98–101. https://doi.org/10.1111/1467-8721.ep10768783
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Mukaka, M. M. (2012). Statistics corner: A guide to appropriate use of correlation coefficient in medical research. Malawi Medical Journal, 24(3), 69–71.
Rumsey, D. J. (2023, 6 de fevereiro). What is r value correlation? Dummies. https://www.dummies.com/article/academics-the-arts/math/statistics/how-to-interpret-a-correlation-coefficient-r-169792/
Schober, P., Boer, C., & Schwarte, L. A. (2018). Correlation coefficients: Appropriate use and interpretation. Anesthesia and Analgesia, 126(5), 1763–1768. https://doi.org/10.1213/ANE.0000000000002864
Como citar este post
Lima, M. (2021, 11 de fevereiro). O que é correlação de Pearson? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-e-correlacao-de-pearson/














Respostas de 2
O coeficiente de correlação representado pela letra “r” pode variar entre -1 e +1. Quando os valores “r” são negativos, a correlação é classificada como do tipo inversa, já quando os valores de “r” são positivos a correlação é direta.
essa afirmativa é correta ?
sou estudante de farmácia
Oi, Luiz. Sim, o termo inversa está correta, mas sugiro evitar o termo relação “direta” para a correlação positiva. Geralmente os termos mais usuais são simplesmente correlação positiva e negativa mesmo.