O coeficiente de correlação de postos de Spearman é uma estatística não paramétrica que mede a dependência entre postos de duas variáveis. Neste post, você aprenderá o que é a correlação de Spearman, quando usá-la, como calculá-la e como interpretar seus resultados.
Qual é a definição da correlação de Spearman?
O coeficiente de correlação de postos de Spearman também é conhecido como ρ (letra grega rho) de Spearman, rs de Spearman ou, simplesmente, correlação de Spearman. Esse coeficiente descreve a relação entre os postos de duas variáveis que estão monotonicamente relacionadas.
Por exemplo, suponha que cinco amigas instalaram um contador de passos em seus celulares e compartilharam seus resultados umas com as outras após a primeira semana de uso do aplicativo. A Figura 1 resume as distâncias e tempos percorridos por cada uma das cinco amigas.
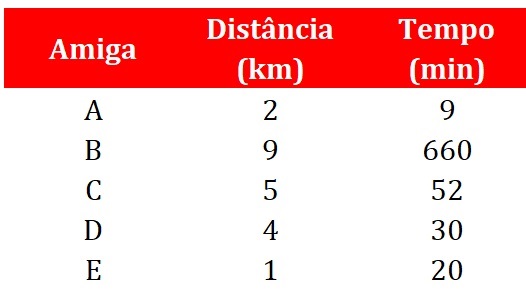
Uma inspeção da Figura 1 sugere que a distância percorrida aumenta conforme o tempo percorrido também aumenta. De fato, o coeficiente de correlação de Pearson entre as duas variáveis indica uma correlação forte, atingindo o nível convencional de significância de 0,05, isto é, r = 0,88, p = 0,046. No entanto, a relação entre as variáveis não parece ser linear (veja a Figura 2).
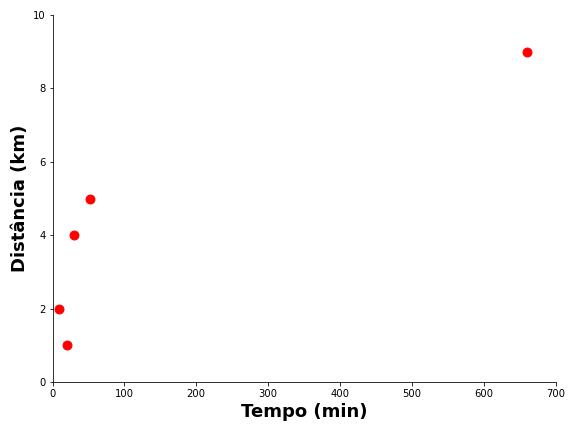
Isso ocorre principalmente por causa da amiga B, que percorreu uma distância quase duas vezes maior que a segunda amiga mais ativa da semana, mas para isso precisou se movimentar mais de 10 vezes mais tempo (ou seja, a velocidade dela foi baixa).
Como veremos, a consequência de a relação entre as variáveis das Figura 1 e 2 ser não linear é que a correlação de Pearson subestima a força da relação entre elas. Por isso, em tais casos, é melhor usarmos a correlação de Spearman.
Contudo, para melhor entendimento da correlação de Spearman, antes vamos entender os significados dos termos postos e relação monotônica.

O que são postos?
Uma solução para o problema anteriormente apresentado é tentarmos “linearizar” a relação entre as variáveis antes de calcularmos o coeficiente de correlação. Em síntese, postos consistem em transformações da variável original.
A transformação em postos é bastante simples: em cada uma das variáveis de interesse, os participantes são ranqueados (o termo postos vem do inglês, ranks), atribuindo-se o posto 1 ao menor escore, o posto 2 ao segundo menor escore, e assim por diante. A Figura 3 apresenta os postos das duas variáveis.
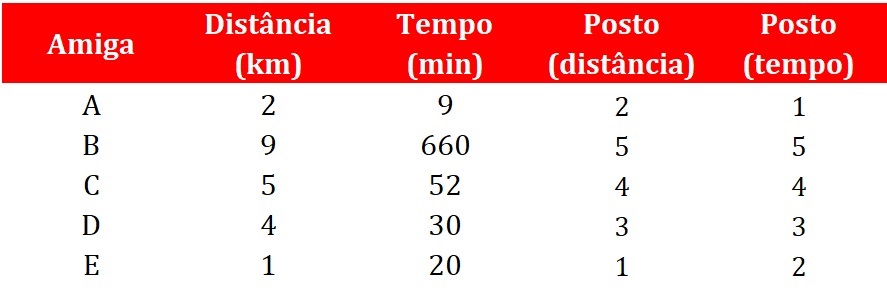
Com base na transformação em postos mostrada na Figura 3, agora as variáveis passaram a ser descritas em nível ordinal: os postos representam a posição relativa de cada amiga, da mais inativa (recebendo postos menores) até a mais ativa (recebendo postos maiores).
A consequência dessa transformação é que as posições relativas entre as amigas são preservadas, mas não as distâncias relativas de seus escores. Por exemplo, consideremos apenas a variável tempo percorrido: a diferença absoluta entre as amigas B e C (660 – 52 = 608 min) é bem maior que a diferença entre as amigas C e D (52 – 38 = 14 min). Por outro lado, as diferenças relativas, em termos de postos, é igual a 1 nos dois casos (isto é, 5 – 4 = 4 – 3 = 1).
O que é relação monotônica?
Monotonicidade é um conceito matemático relacionado a funções entre conjuntos. A relação entre X e Y é monotônica crescente quando, para todos os pares de valores de X, em que x1 ≤ x2, o mesmo ocorre em Y, em que y1 ≤ y2.
Em outras palavras, sempre que o valor de uma variável aumenta, o valor da outra variável também aumenta ou se mantém constante. Se o tempo de movimento aumenta e a distância percorrida também aumenta ou se mantém igual, então temos uma relação monotônica crescente.
Por outro lado, a relação entre X e Y é monotônica decrescente quando, para todos os pares de valores de X, em que x1 ≤ x2, o oposto ocorre em Y, em que y1 ≥ y2.
Em outras palavras, sempre que o valor de uma variável aumenta, o valor da outra variável diminui ou se mantém constante. Se o tempo de movimento aumenta e o percentual de gordura diminui ou se mantém igual, então temos uma relação monotônica decrescente.
O ponto essencial é que a monotonicidade entre duas variáveis é um pressuposto menos restritivo que a linearidade, pois leva em consideração apenas a ordem dos postos nas duas variáveis. Isto é, duas variáveis com relação linear também têm relação monotônica, mas variáveis com relação monotônica podem não estar linearmente relacionadas.
A Figura 4 ilustra a relação monotônica (mas não linear) entre duas variáveis, bem como a relação linear (e também monotônica) entre duas variáveis.
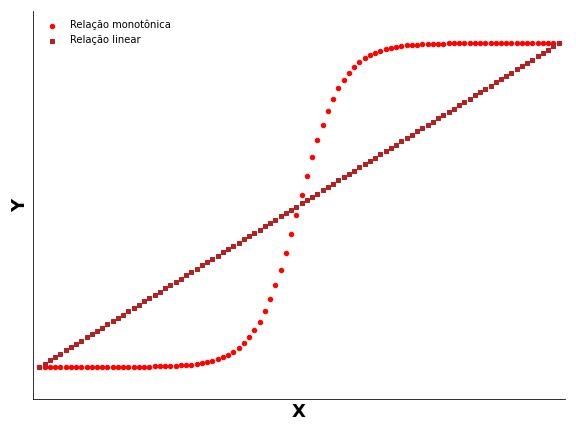
Importante, a correlação de Pearson estima a força e a direção da relação entre variáveis linearmente relacionadas, enquanto a correlação de Spearman faz o mesmo para variáveis monotonicamente relacionadas.
Como calcular a correlação de Spearman?
Em sua prática cotidiana, você provavelmente jamais precisará calcular manualmente a correlação de Spearman. No entanto, do ponto de vista didático, apresentaremos os cálculos do exemplo anterior das cinco amigas.
Na prática, depois de computar os postos, o algoritmo do coeficiente de correlação de Spearman calcula as diferenças entre postos para cada observação, e eleva essas diferenças ao quadrado. A Figura 5 ilustra essas etapas.
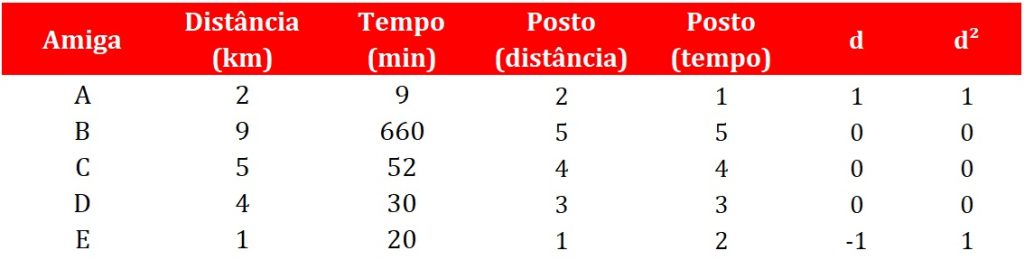
Por exemplo, atribuímos o posto 1 à amiga E na variável distância, e o posto 2, na variável tempo, o que resulta em d = – 1 e d2 = 1. O mesmo é feito para as demais amigas. Por fim, o coeficiente de correlação de Spearman é calculado por meio da seguinte equação:
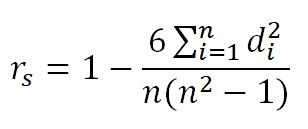
onde d2 corresponde às linhas da última coluna da Figura 5, i corresponde a cada uma das linhas da Figura 5 e n corresponde ao tamanho amostral. Para os dados da Figura 5, temos o seguinte resultado:
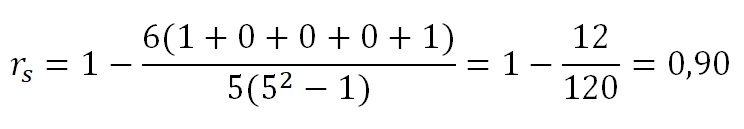
Ou seja, o valor de rs = 0,90 indica que a correlação monotônica entre as variáveis é forte e, inclusive, superior àquela estimada pela correlação de Pearson, que havia sido de r = 0,88.
Como interpretar o coeficiente de correlação de Spearman?
A correlação de Spearman sumariza a relação entre duas variáveis por meio de um número que varia de –1 a +1. Quanto mais próximo dos extremos (–1 ou +1), maior é a força da relação monotônica entre variáveis. Já os valores próximos de 0 indicam correlações mais fracas ou inexistentes.
No entanto, também precisamos interpretar o sinal do coeficiente, que indica a direção dessa relação. Se positiva, o aumento em uma variável está associado ao aumento na outra variável. Os valores negativos indicam que o aumento de uma variável está associado ao decréscimo na outra outra.
Alguns valores de correlação de Spearman, e seus respectivos diagramas de dispersão, são sumarizados na Figura 6.

Posso interpretar relações não lineares com a correlação de Spearman?
Uma vez que a correlação de Spearman se foca em relações monotônicas e não tem pressupostos lineares, como na correlação de Pearson, é possível utilizá-la para sumarizar relações não lineares. Por isso, nos dados da Figura 7, a correlação de Spearman é mais eficaz em identificar a relação entre as variáveis que a correlação de Pearson.
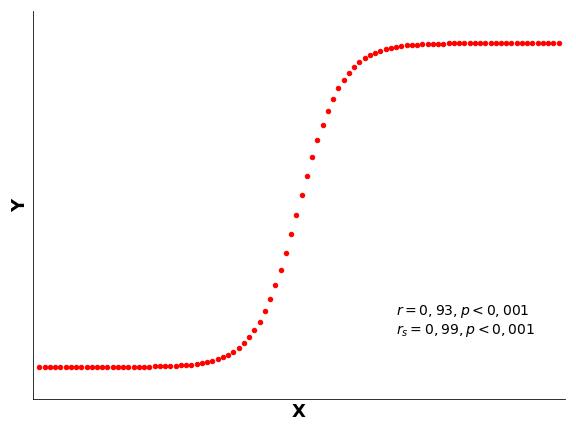
Embora ambos os coeficientes indiquem correlação significativa entre o par de variáveis da Figura 7, a correlação de Pearson subestima a relação entre variáveis, quando comparada à correlação de Spearman. Isso ocorre, como já vimos anteriormente, porque a linearidade, tal como assumida pela correlação de Pearson, é um pressuposto mais restritivo que a monotonicidade, assumida pela correlação de Spearman.
Como interpretar os coeficientes de correlação de Spearman?
Até aqui, você já deve ter uma noção de como interpretar a direção e a força da correlação de Spearman, mas pode querer uma interpretação mais objetiva do significado dos números apresentados nos testes de correlação. Contudo, não existe consenso sobre o a interpretação dos valores da correlação. O que existem, de fato, são algumas recomendações.
Cohen (1992), por exemplo, sugere os seguintes pontos de corte:
- rs = |±0,10| → correlação fraca;
- rs = |±0,30| → correlação moderada;
- rs = |±0,50| → correlação forte.
Por outro lado, Rumsey (2023) traz a seguinte sugestão de tamanhos de efeito:
- rs = |±1| → relação linear perfeita;
- rs = |±0,70| → relação linear forte;
- rs = |±0,50| → relação linear moderada;
- rs = |±0,30| → relação linear fraca;
- rs = 0 → ausência de relação linear.
Note que as interpretações são simétricas, independentemente de o coeficiente ser positivo ou negativo. Além disso, as sugestões acima não são prescritivas. Isto quer dizer, portanto, que pesquisadores devem sempre interpretar seus coeficientes à luz da literatura de suas respectivas áreas de pesquisa.
Como avaliar a correlação através do coeficiente de determinação?
Podemos ter uma melhor noção do significado da correlação através do coeficiente de determinação (rs2), que indica o quanto uma variável encontra-se associada à outra em termos de percentual de variância compartilhada.
O rs2 é calculado simplesmente elevando rs ao quadrado. Por exemplo, se rs2 = 0,80, então 64% da variância de uma variável pode ser explicada pela outra, pois rs2 = 0,802 = 0,64 (multiplicamos o valor por 100, para que ele seja expresso em termos percentuais). Se rs2 = 0,90, então 81% da variância de uma variável pode ser explicada pela outra, pois rs2 = 0,902 = 0,81. A Figura 8 apresenta outros valores de coeficientes de determinação.
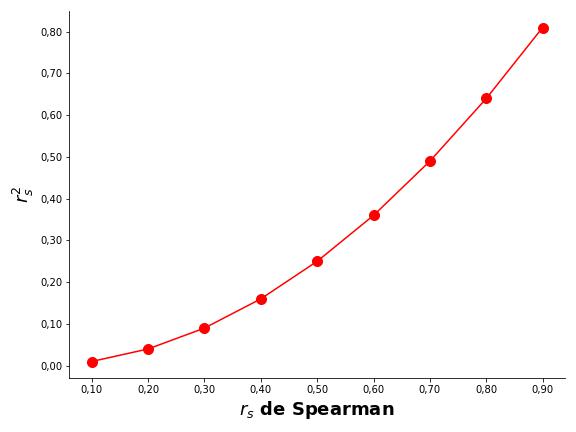
Por isso, interpretar o rs2 pode trazer maior clareza sobre o quanto os construtos encontram-se relacionados. Contudo, é importante atenção, pois à medida que o coeficiente de correlação vai aumentando, a variância compartilhada cresce exponencialmente (veja a Figura 8). Por exemplo, a diferença de variância explicada entre os coeficientes de correlação de 0,10 para 0,20 é de apenas 3% (0,04 – 0,01 = 0,03). Entretanto, entre rs = 0,80 e rs = 0,90, a diferença na variância explicada já é de 17% (0,81 – 0,64 = 0,17).
É importante destacar que, para a interpretabilidade do tamanho do efeito das correlações, você pode se basear nas diretrizes mencionadas, mas é a revisão de literatura que irá, de fato, lhe informar se os seus achados são fracos ou fortes. Lembre-se de interpretar os tamanhos de efeito de seu estudo sempre à luz da literatura de sua área de pesquisa.
Conclusão
Neste post, você aprendeu mais sobre a correlação de Spearman, uma das formas de realizar análises de correlação entre variáveis. Se você procura analisar relações lineares, o coeficiente de Pearson é o mais adequado, como explicamos neste post. Outra medida não paramétrica que pode te interessar é o τ (letra grega tau) de Kendall.
Gostou desse conteúdo? Quer aprender mais sobre análise de correlação? Então confira também nossos posts sobre correlação ponto-bisserial, correlação parcial e correlação policórica.
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Cohen, J. (1992). Statistical power analysis. Current Directions in Psychological Science, 1(3), 98–101. https://doi.org/10.1111/1467-8721.ep10768783
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Mukaka, M. M. (2012). Statistics corner: A guide to appropriate use of correlation coefficient in medical research. Malawi Medical Journal, 24(3), 69–71.
Rumsey, D. J. (2023, 6 de fevereiro). What is r value correlation? Dummies. https://www.dummies.com/article/academics-the-arts/math/statistics/how-to-interpret-a-correlation-coefficient-r-169792/
Schober, P., Boer, C., & Schwarte, L. A. (2018). Correlation coefficients: Appropriate use and interpretation. Anesthesia and Analgesia, 126(5), 1763–1768. https://doi.org/10.1213/ANE.0000000000002864
Como citar este post
Lima, M. (2021, 14 de fevereiro). O que é correlação de Spearman? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-e-correlacao-de-spearman/














Respostas de 5
Como seria o calculo do Correlação de Spearman?
Olá, Marcos. Veja que atualizamos o post, incluindo a fórmula e um exemplo de como realizar o cálculo. Há outros post no blog mostrando como executar a análise no JASP.
Equipe Psicometria Online.
quando di=0 como faço?
Oi, Carlos. Por di, você se refere à diferença dos postos das duas variáveis? Se for essa a dúvida, isso não é um problema. Na verdade, se os di’s de todos os participantes for igual a 0, isso fará com que o rhô de Spearman seja igual a 1 (correlação perfeita entre os postos das duas variáveis).
Equipe Psicometria Online.
Excelente professor Bruno Damásio.
Conteúdo bem explicativo de forma clara e concisa!