Neste post, você aprenderá sobre o gráfico de Bland-Altman, uma representação útil para avaliar a concordância entre dois métodos de mensuração da mesma quantidade subjacente. Primeiramente, descreveremos o cenário em que tipicamente queremos avaliar a concordância entre métodos. Em seguida, apresentaremos o gráfico de Bland-Altman e seus principais elementos. Por fim, nós mostraremos o passo a passo de como construir o gráfico de Bland-Altman, além de darmos dicas gerais de como interpretá-lo.
Avaliação da concordância entre dois métodos
A fim de determinar se dois métodos de mensuração são intercambiáveis entre si, pesquisadores podem aferir o grau de concordância entre eles. Por exemplo, pesquisadores mensuram a pressão arterial sistólica de um grupo de pacientes usando um esfigmomanômetro ou um monitor de pressão semiautomático.
Em seguida, eles almejam avaliar se a concordância entre os dois métodos de mensuração são equivalentes o suficiente para podermos investigar mudanças clínicas relevantes. Esse objetivo de pesquisa é importante, pois um dos métodos de mensuração pode ser mais demorado ou mais caro que o outro. Ou seja, se pesquisadores demonstrarem que o método mais rápido e barato for equivalente ao outro método, eles podem substituí-lo sem prejuízos para a tomada de decisão clínica.
Anteriormente, falamos sobre métodos de mensuração. Contudo, o “método” pode consistir em diferentes avaliadores. Por exemplo, se dois assistentes de pesquisa mensuram de maneira independente o peso de ratos em um estudo laboratorial, cada avaliador pode ser considerado um “método”, e nosso interesse é avaliar se os pesos aferidos pelos dois avaliadores concordam entre si.
Em tais casos, técnicas que avaliam a concordância são úteis. Por exemplo, quando as medidas avaliadas são categóricas, podemos quantificar a concordância por meio do kappa de Cohen. No entanto, quando as medidas são contínuas, o gráfico de Bland-Altman é mais apropriado.

O que é o gráfico de Bland-Altman?
O gráfico de Bland-Altman (Bland–Altman plot) é um tipo especial de diagrama de dispersão. Em síntese, ele permite avaliar: (a) os limites de concordância (tipicamente, de 95%) entre os dois métodos de mensuração; (b) o viés entre dois métodos de mensuração; e (c) se o viés é ou não constante ao longo da escala de mensuração.
A Figura 1 apresenta um exemplo de gráfico de Bland-Altman. Ele plota a média de cada participante nas duas medidas sob comparação, no eixo x, versus a diferença entre essas duas medidas, no eixo y.
Em seguida, mostraremos como construir esse gráfico.
Como criar um gráfico de Bland-Altman?
Primeiramente, nosso exemplo se baseia em dados publicamente disponíveis em Hirakata e Camey (2010). Dois métodos foram usados para estimar o tempo de gestação de 50 mulheres, a saber, via data da última menstruação e via ultrassom. A Figura 2 mostra algumas das linhas desse banco de dados.
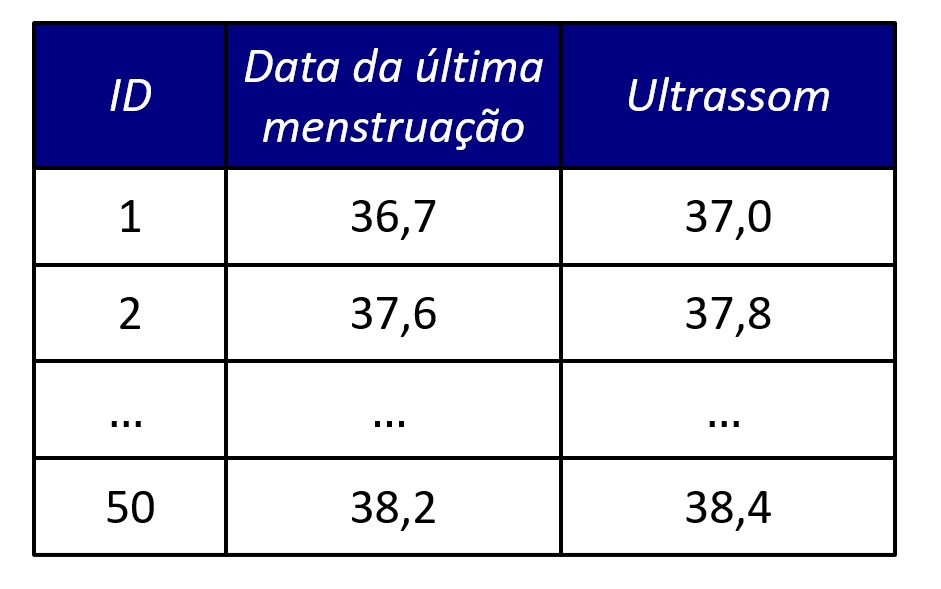
Note que, na Figura 2, os valores contidos em cada linha consiste no número de semanas estimadas de gestação conforme dois métodos distintos.
Calculando a média e a diferença das medidas
Com base nesses valores brutos, calcularemos a média das estimativas obtidas pelos dois métodos, bem como a diferença entre eles.
As médias de cada participante são nossas melhores estimativas dos escores verdadeiros de cada gestante. Sua fórmula é a seguinte:
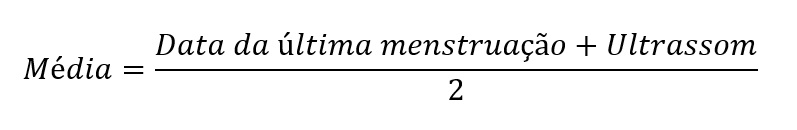
Por outro lado, a diferença das medidas indica o viés de um método em relação ao outro (i.e., se um método produz escore maior que o outro). Sua fórmula é a seguinte.
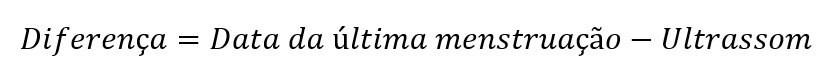
A Figura 3 reapresenta os dados da Figura 2, mas agora com as colunas média e diferença.
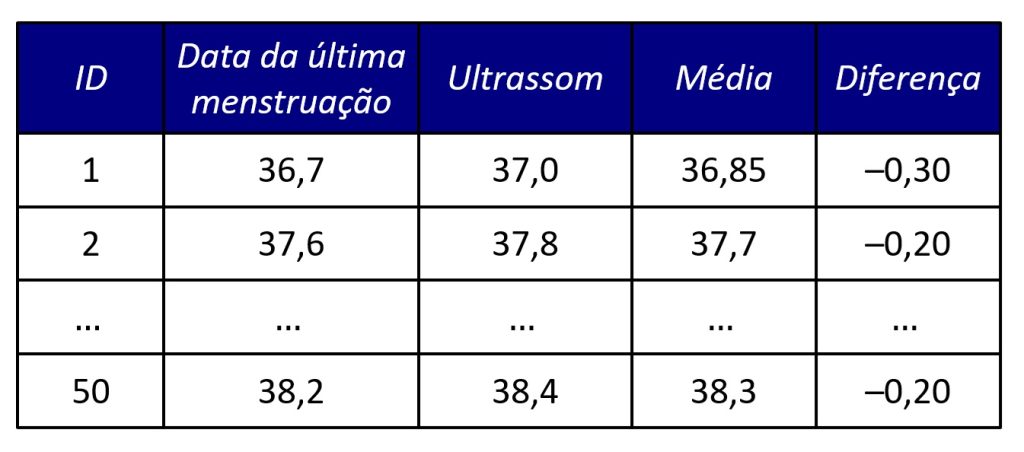
Note que, ao menos para os casos apresentados na Figura 3, as diferenças foram sempre negativas. Em outras palavras, o método do ultrassom forneceu estimativas de tempo de gestão mais elevadas que o método da data da última menstruação, ao menos para os casos da Figura 3.
Plotando a média e a diferença das medidas em um diagrama de dispersão
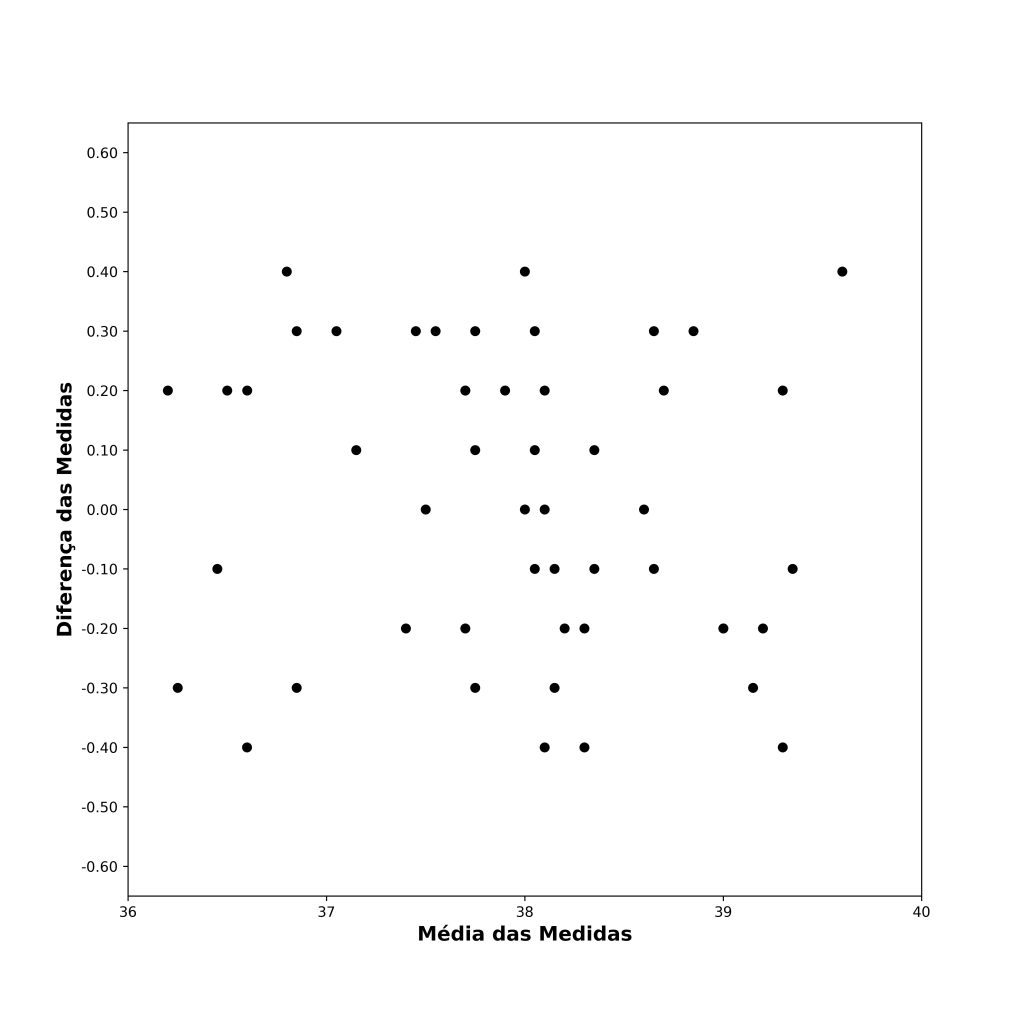
Em seguida, começaremos a plotar nosso gráfico de Bland-Altman. Cada par ordenado de valores (média, diferença) será plotado como um ponto em um plano cartesiano. Desse modo, o início de nosso gráfico será um diagrama de dispersão, com a média das medidas no eixo x, e a diferença das medidas, no eixo y (Figura 4).
Em seguida, podemos calcular a média da coluna diferenças, que será a nossa estimativa de viés, a tendência consistente de um método em produzir escores mais elevados que o outro.
Em nosso exemplo, o valor obtido foi de 0,014. Quanto mais distante de zero, maior será o viés de um dos métodos de mensuração sobre o outro. Na prática, podemos avaliar se o viés difere estatisticamente de zero por meio de um teste t para amostra única.
A direção do viés dependerá da ordem de subtração dos métodos de mensuração no eixo y. O valor de viés é plotado como uma linha pontilhada no centro do gráfico (Figura 5).
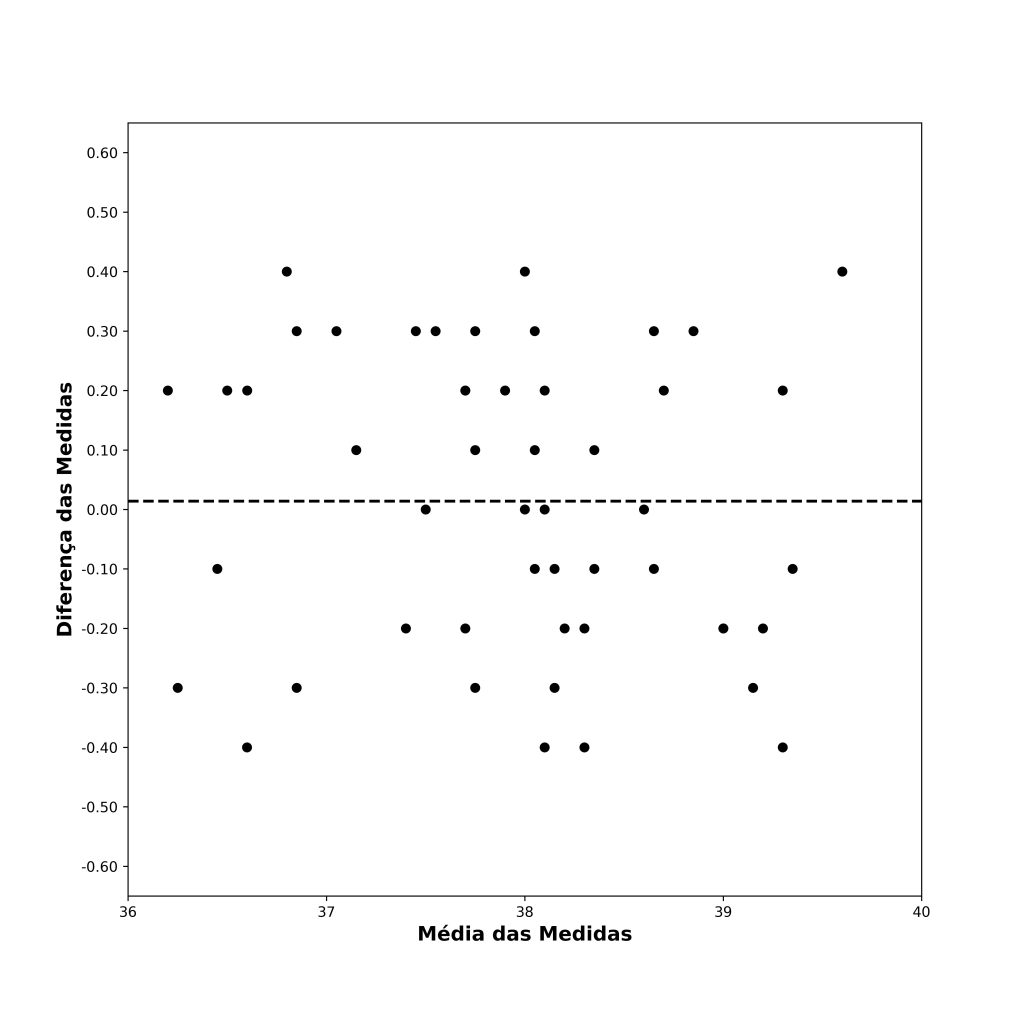
Por fim, fazemos uma breve análise do padrão dos pontos no diagrama. Pontos com um padrão aleatório na Figura 5 indicam diferenças consistentes ao longo da escala de mensuração. Contudo, teríamos um problema se o padrão de dispersão dos pontos fosse heterocedásticos em relação à linha de viés, ou se indicassem associação entre as variáveis nos dois eixos.
Plotando os limites de concordância no gráfico de Bland-Altman
Em seguida, calcularemos e plotaremos os limites de concordância:
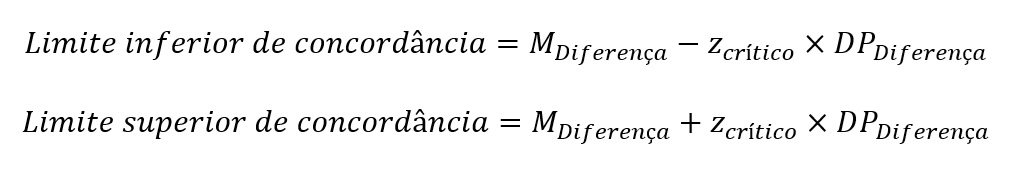
Onde o zcrítico depende do percentual de concordância almejado; se 95%, então z = 1,96. O valor de DPDiferença representa flutuações aleatórias ao redor do viés, consistindo no desvio-padrão da coluna Diferença, na Figura 3. Os valores obtidos são –0,47 e 0,51, que são plotados como linhas pontilhadas na Figura 6.
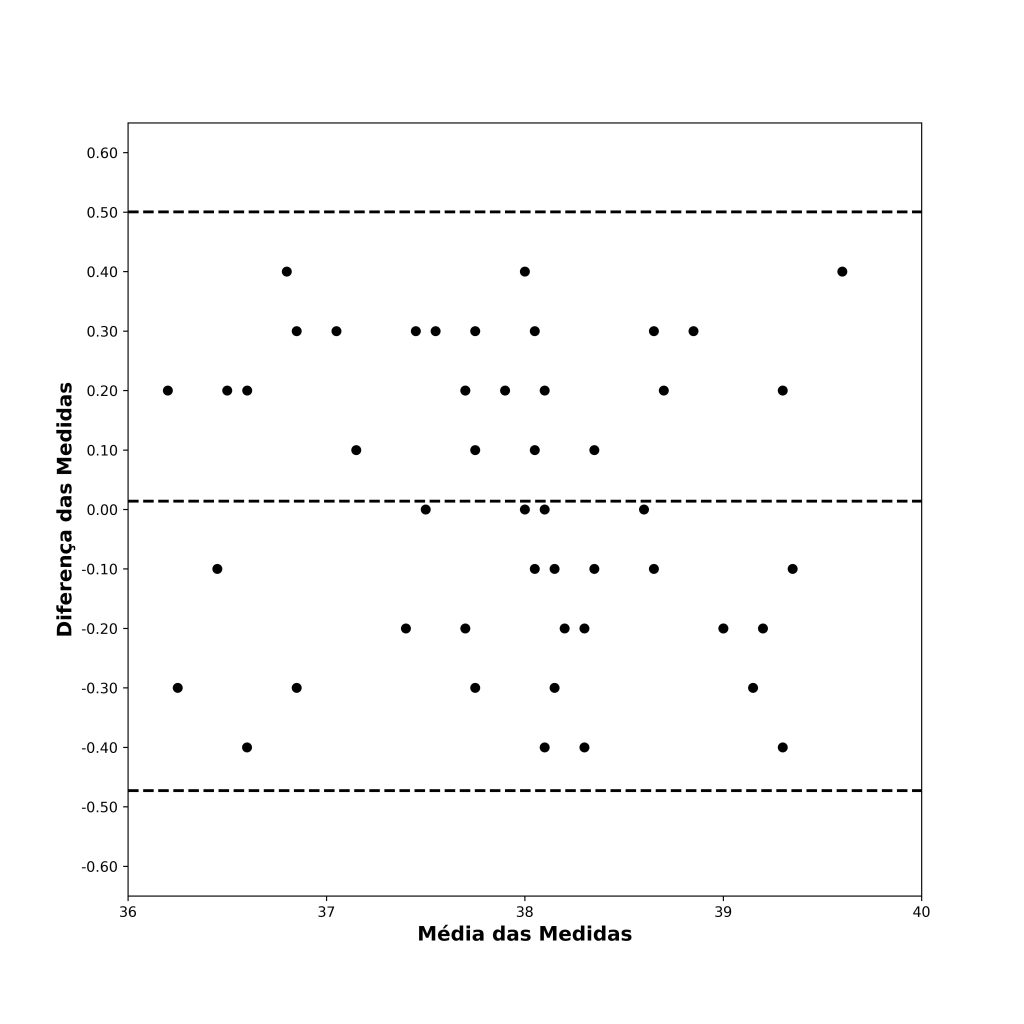
Contudo, note que esses valores não representam intervalos de confiança. Ao invés disso, eles indicam quais magnitudes de diferenças entre os métodos nós mais provavelmente observaremos, apenas devido ao erro de mensuração. Entretanto, essa interpretação só é válida se pudermos pressupor que as diferenças das medidas estão normalmente distribuídas.
Dizemos que os métodos são intercambiáveis quando diferenças dentro dos limites de concordância não são clinicamente relevantes.
Por exemplo, suponha que queremos investigar o efeito de uma intervenção sobre uma determinada medida. No entanto, o efeito esperado por nossa intervenção é de apenas 0,20 unidade. Como esse valor está dentro dos limites de concordância entre métodos de mensuração (Figura 6), não seremos capazes de detectá-la. Isso ocorre porque a nossa menor mudança clinicamente detectável será dada pela amplitude dos limites de concordância do gráfico de Bland-Altman.
Plotando intervalos de confiança ao redor das estimativas
Os valores de viés e de limites de concordância são estimativas amostrais. Em outras palavras, eles estão sujeitos a flutuações em amostragens repetidas, tais como outras estatísticas que comumente calculamos em nossas pesquisas.
Sendo assim, podemos quantificar a precisão dessas estimativas em nossa amostra. Para esse fim, calcularemos e plotaremos intervalos de confiança ao redor de nossas estimativas. Leitores interessados podem consultar as fórmulas em Bland e Altman (1999, p. 142).
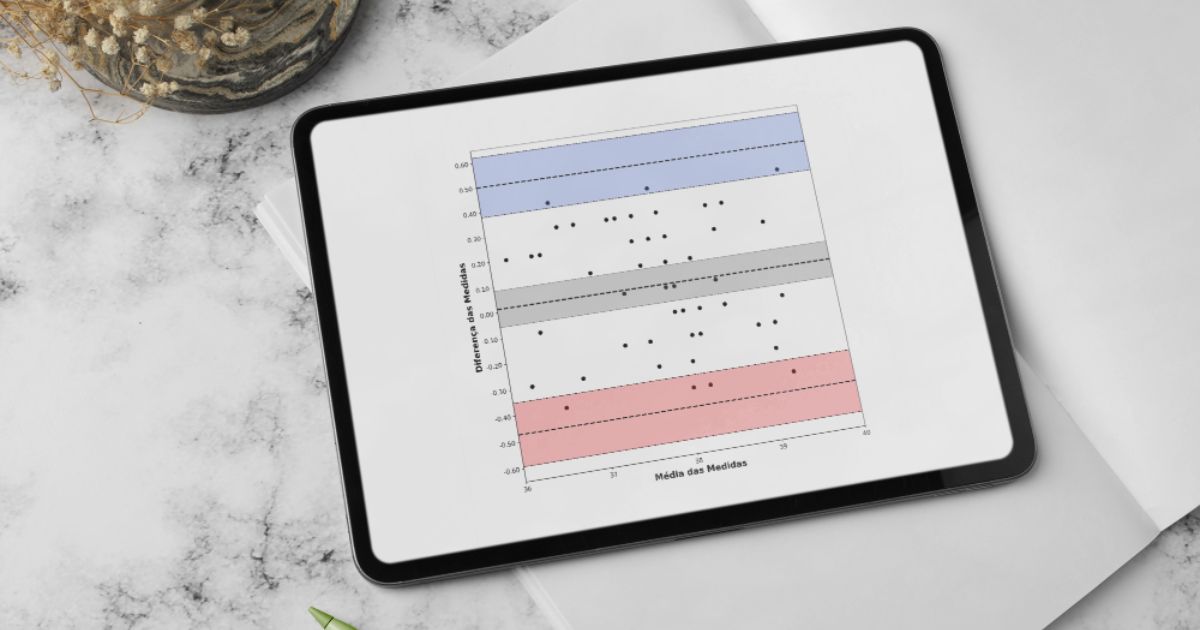
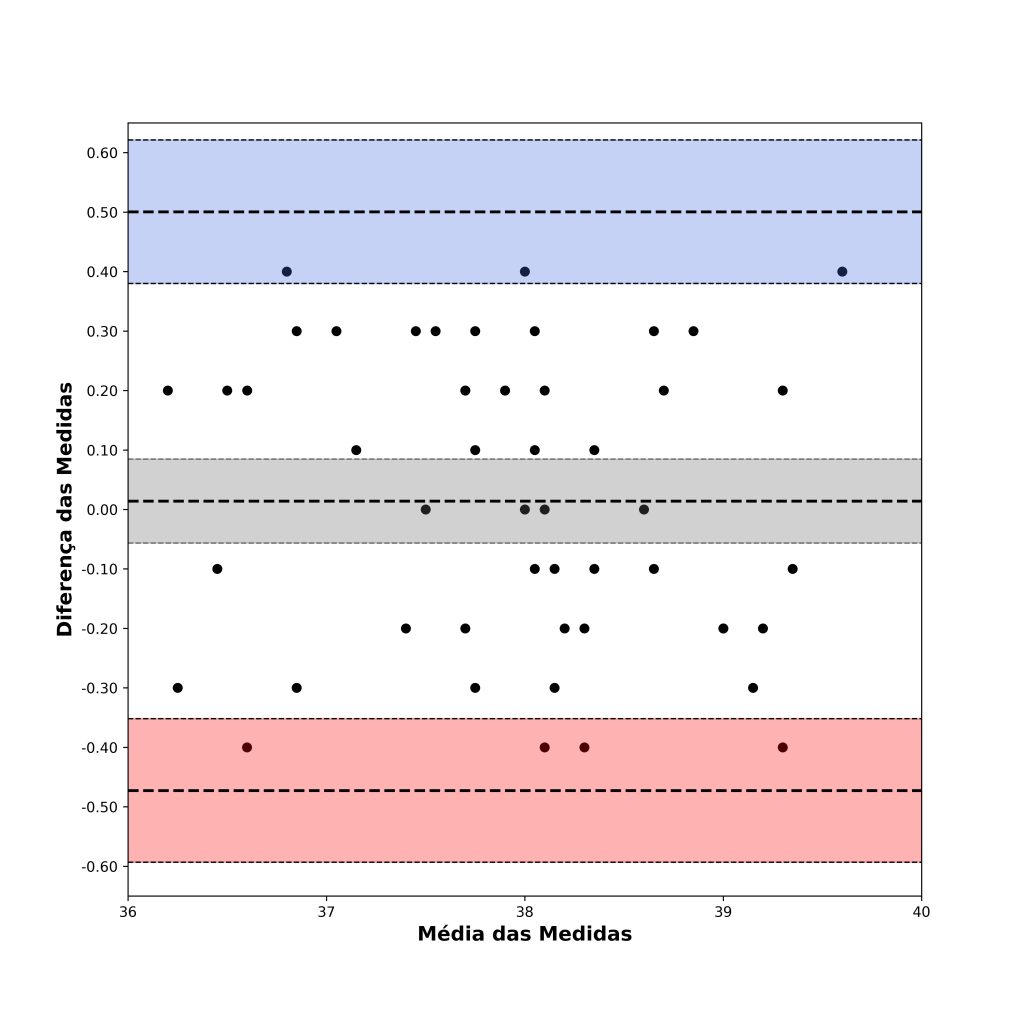
A Figura 7 apresenta três intervalos de confiança: de cima para baixo, as linhas pontilhadas finas representam os intervalos de confiança para (a) o limite superior de concordância, (b) o viés e (c) o limite inferior de concordância.
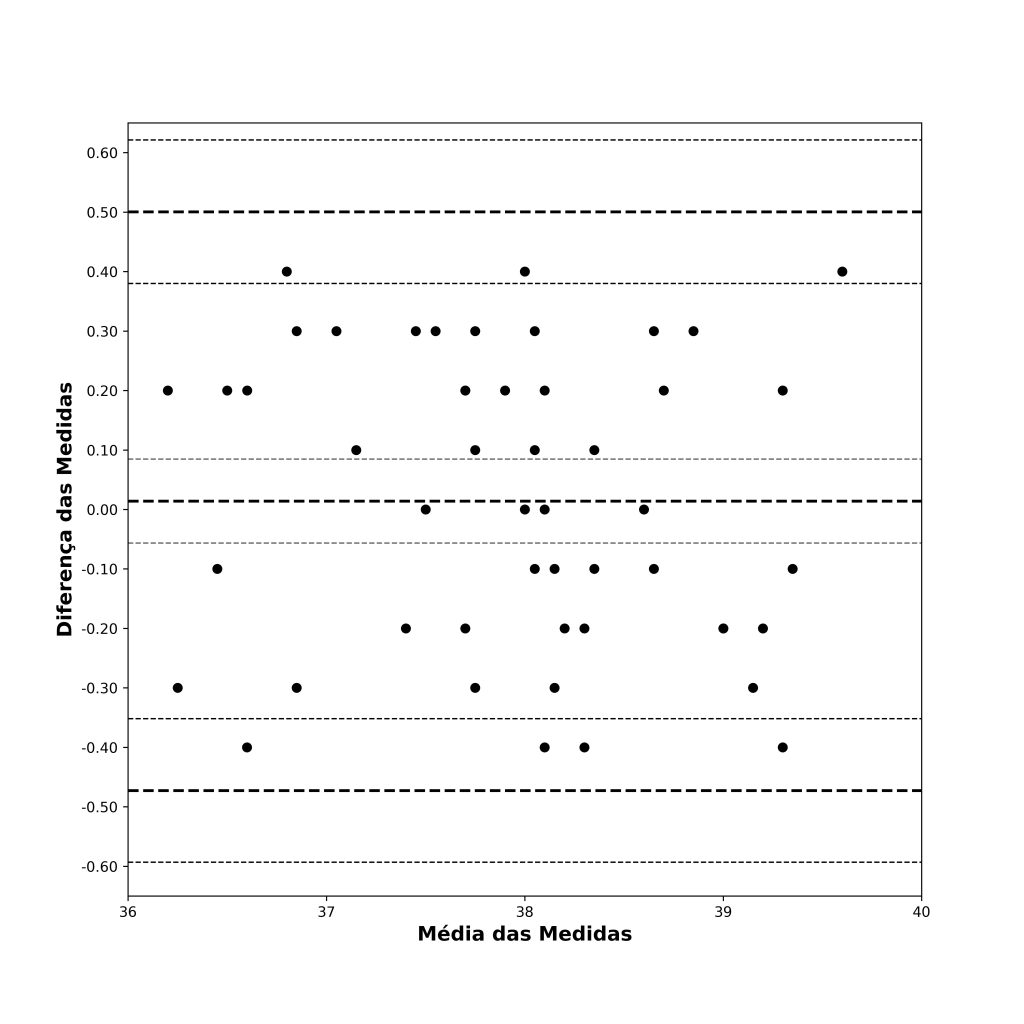
Uma maneira de melhorar a visualização desses intervalos de confiança é sombreá-los com cores distintas, conforme mostramos na Figura 8.
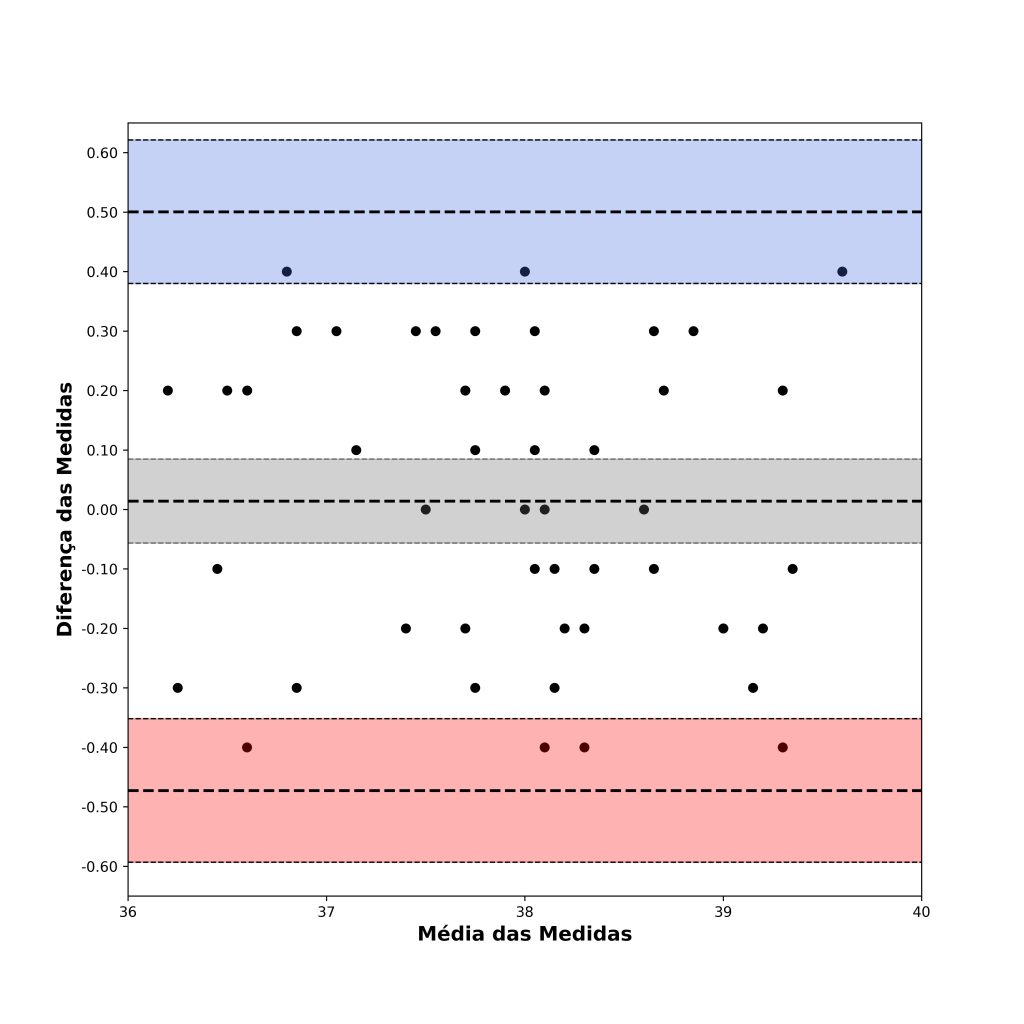
Em nosso exemplo, a estimativa mais otimista dos limites de concordância diz respeito ao limite superior do intervalo de confiança do limite inferior de concordância e ao limite inferior do intervalo de confiança do limite superior de concordância, isto é, um limite de concordância entre –0,352 e 0,380 (o começo e o fim das regiões brancas da Figura 8).
Esses limites são aceitáveis o suficiente para não causar problemas em interpretações clínicas? A resposta a esse pergunta, é claro, dependerá de julgamento clínico. Por exemplo, se queremos avaliar um efeito que é de 2 ou mais semanas de gestação, então podemos considerar os limites de concordância como aceitáveis para investigarmos mudanças clinicamente relevantes.
Exemplos de gráficos de Bland-Altman
Suponha que nossos métodos de mensuração, sejam eles quais forem, produzem valores idênticos entre si. A Figura 9 ilustra esse cenário ideal.
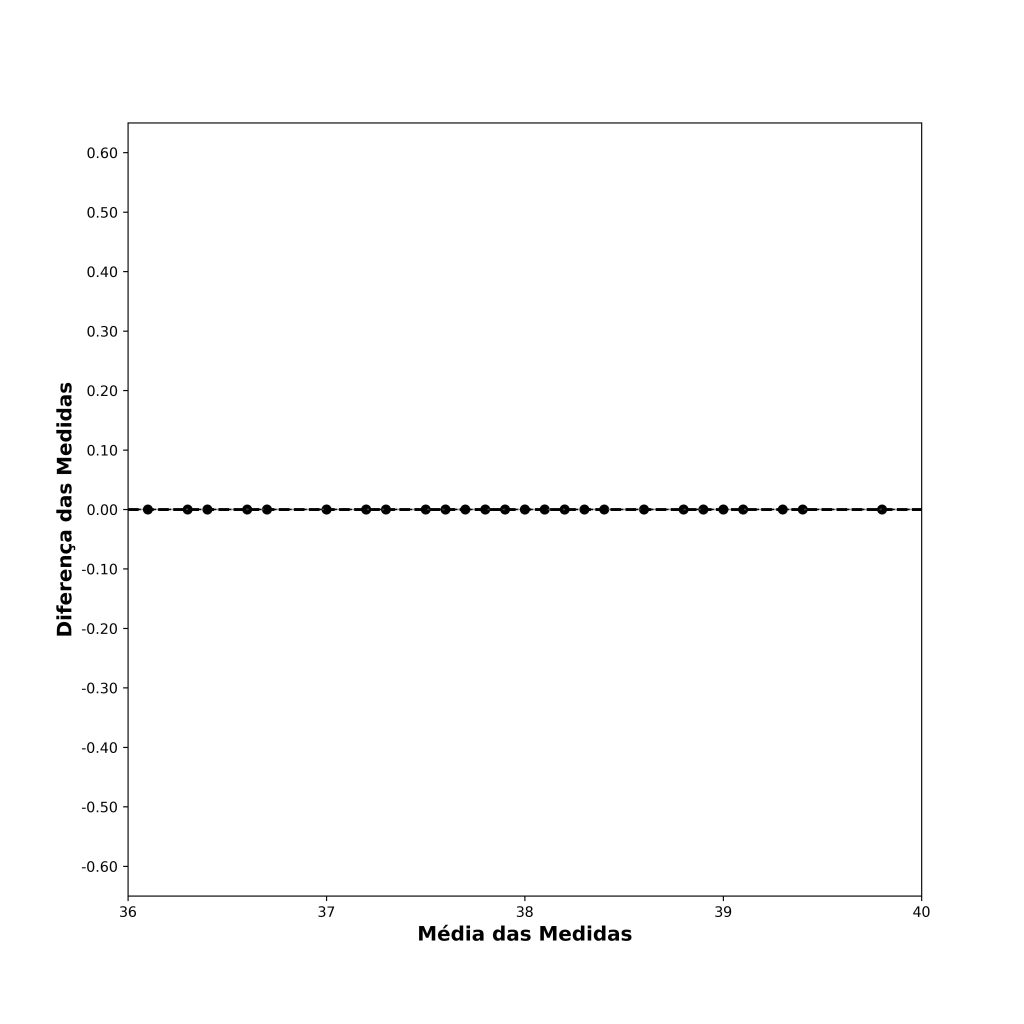
Quando os métodos produzem escores totalmente concordantes, as médias das medidas serão os próprios valores, e, portanto, todas as diferenças das medidas serão iguais a 0. Logo, concluímos que, quanto maior é a concordância, menor será o viés, e mais próxima a linha do viés estará de zero.
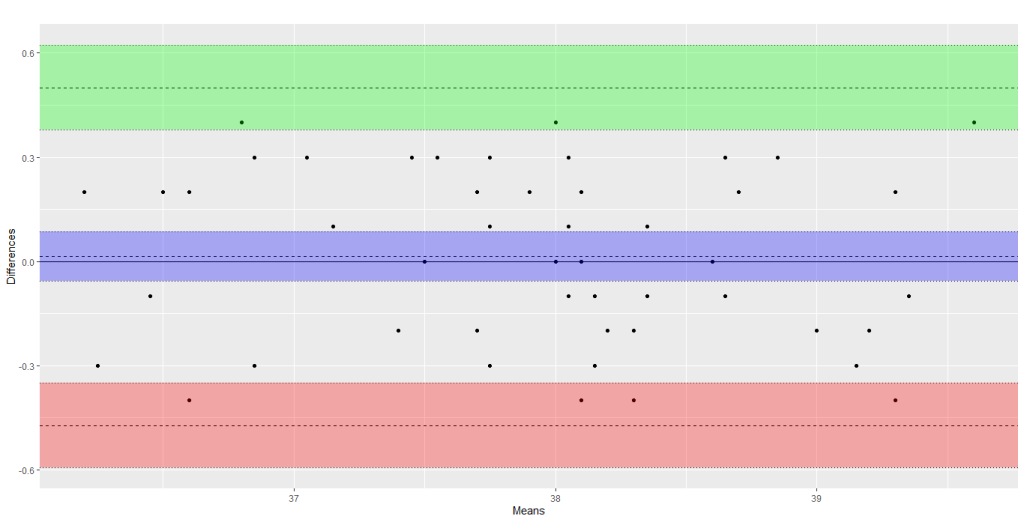
Um pressuposto do gráfico de Bland-Altman é de que o viés e a variabilidade são uniformes ao longo de toda a escala de mensuração da quantidade de interesse. No entanto, esse pressuposto pode estar incorreto, pois o viés pode variar em função da escala de mensuração, conforme exemplificamos na Figura 10.

Reconhecidamente, o exemplo da Figura 10 é um tanto exagerado. Contudo, em casos mais sutis, um teste formal desse pressuposto pode ser feito por meio de uma regressão linear simples, onde inserimos a média das medidas como variável preditora, e a diferença entre elas, como variável critério.
Se o coeficiente de inclinação for estatisticamente significativo, então isso quer dizer que temos viés proporcional. Desse modo, os limites de concordância clássicos são inadequados, devendo ser substituídos por limites de concordância baseados em regressão (veja Bland & Altman, 1999, pp. 145–148).
Onde criar o gráfico de Bland-Altman?
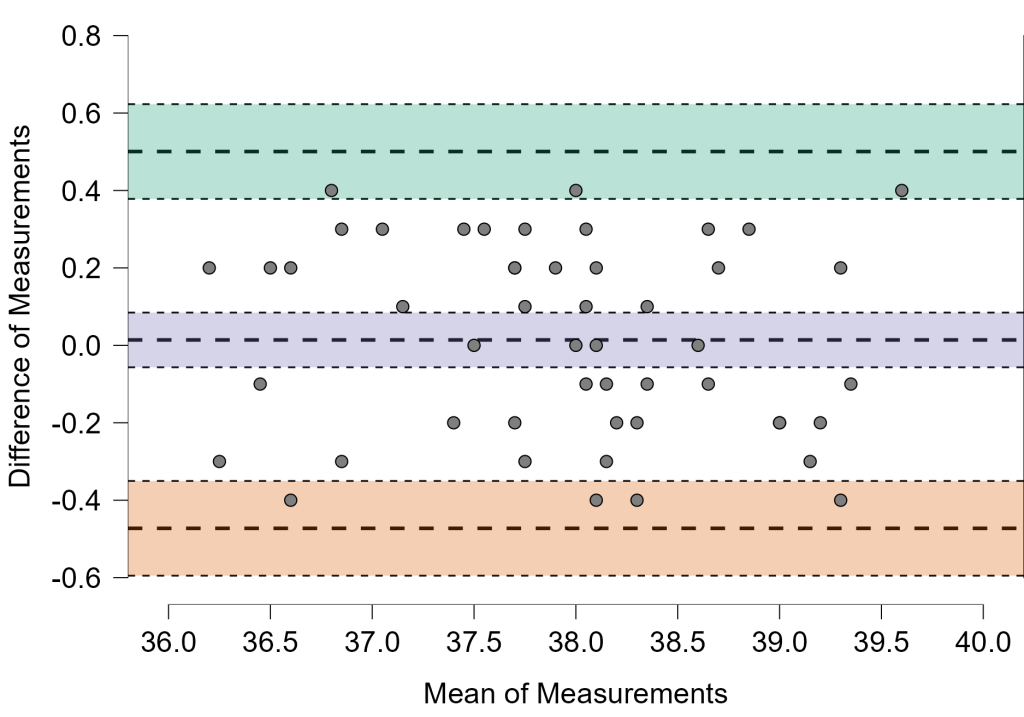
O R permite criar o gráfico de Bland-Altman, por meio da função bland.draw, do pacote blandr. Uma versão sem edições de um gráfico gerado no R é apresentada na Figura 11. Além disso, podemos personalizá-lo ainda mais por meio do pacote ggplot2.
O pacote estatístico JASP também é uma excelente opção gratuita e amigável que pode ser usada para análises estatísticas. Ele não só implementa o gráfico de Bland-Altman, mas também gera as estimativas de viés, limites de concordância e intervalos de confiança em forma tabular. Por exemplo, a Figura 12 foi totalmente criada no JASP.
Conclusão
Neste post, você aprendeu sobre o gráfico de Bland-Altman, o passo a passo para criá-lo e como interpretá-lo.
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Bland, J. M., & Altman, D. G. (1986). Statistical methods for assessing agreement between two methods of clinical measurement. The Lancet, 1(8476), 307–310.
Bland, J. M., & Altman, D. G. (1999). Measuring agreement in method comparison studies. Statistical Methods in Medical Research, 8, 135–160. https://doi.org/10.1177/096228029900800204
Hirakata V. N., & Camey S. A. (2010). Análise de concordância entre métodos de Bland-Altman. Clinical & Biomedical Research, 29(3). https://seer.ufrgs.br/index.php/hcpa/article/view/11727
Como citar este post
Lima, M. (2025, 2 de janeiro). O que é o gráfico de Bland–Altman? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-e-o-grafico-de-bland-altman/