Se você já leu artigos que reportam testes qui-quadrado ou regressões logísticas, é possível que você já tenha se deparado com o termo razão de chances (ou seu equivalente em inglês, odds ratio, OR). Mas o que é chance? E o que é razão de chances? Como calculá-la? E como interpretá-la?
Neste post, responderemos a essas quatro questões.
Veja também:
O que é chance?
A chance (ou seu equivalente em inglês, odds) de um evento ocorrer é definida como a probabilidade p de ocorrência desse evento dividida pela probabilidade q de não ocorrência. Em outras palavras, a chance é a razão entre a probabilidade de um evento acontecer e a probabilidade de ele não acontecer. A Figura 1 ilustra o conceito de chance, relacionando-o ao conceito de probabilidade.
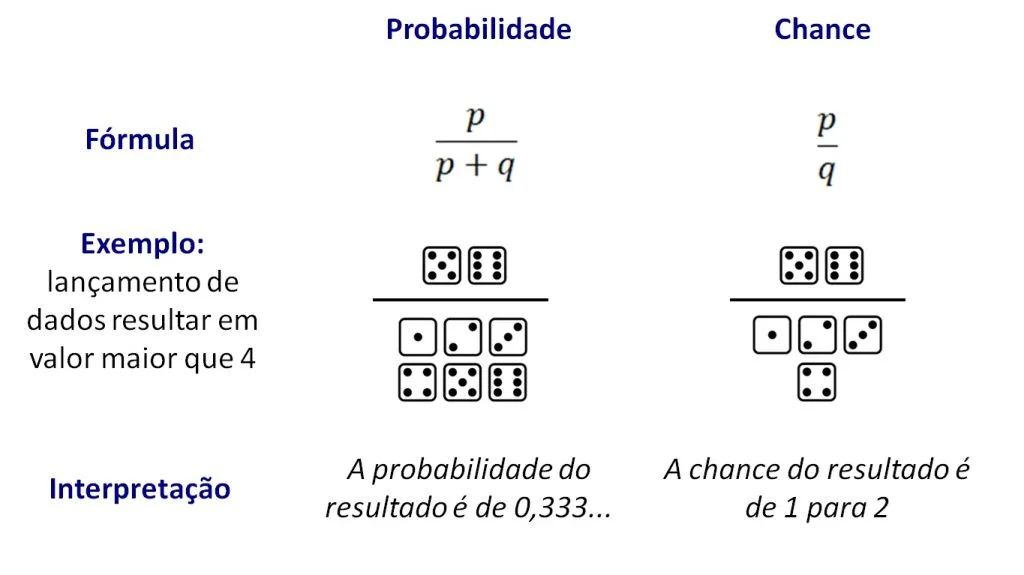
Por exemplo, a probabilidade de obtermos um valor maior que 4 em um lançamento de dados é de 2 em 6, pois há dois valores maiores que 4 em um dado. Para transformar essa probabilidade em chance, dividimos a probabilidade do evento (2 em 6) pela probabilidade do não evento (4 em 6), que resulta em 1/2, ou seja, 0,50.
Em síntese, concluímos que a chance de obtermos um número maior que 4 a partir do lançamento de um dado é de 1 em 2 ou, de forma equivalente, é duas vezes mais provável não obtermos um valor maior que 4, do que obtermos um valor menor ou igual a 4, a partir de um lançamento de dados.

O que é razão de chances?
A razão de chances é uma medida de tamanho de efeito que expressa a força da associação entre as variáveis categóricas X e Y. Ela é definida como a chance de ocorrência de Y na presença de X dividida pela chance de ocorrência de Y na ausência de X.
Por exemplo, considere a hipótese de que existe uma associação entre o consumo de cogumelos mágicos e o relato da observação de objetos voadores não identificados (OVNIs). Em outras palavras, se isso for verdadeiro, quem consome cogumelos mágicos deve ser mais provável do que quem não os consome de reportar já ter visto OVNIs.
Desse modo, a razão de chances avaliaria quantas vezes mais (ou menos) chances alguém que consome cogumelos mágicos tem de reportar já ter visto OVNIs, em comparação a quem não consome tais cogumelos.
Vamos assumir que um pesquisador coletou dados para testar essa hipótese. A Figura 2 ilustra uma tabela de contingências 2 × 2, que mostra o cruzamento entre o número de pessoas que consome ou não cogumelos mágicos e o número de pessoas que alega ou não já ter visto OVNIs.
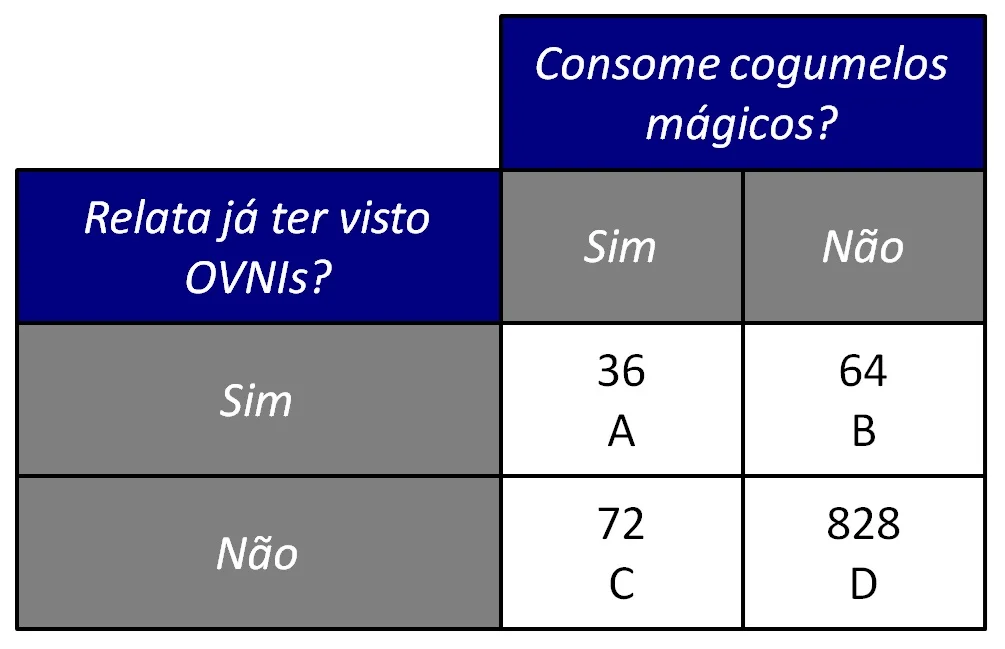
A associação entre as duas variáveis poderia ser testada, por exemplo, por meio de um teste qui-quadrado de independência. A partir desse teste, concluimos que a associação entre as variáveis é estatisticamente significativa, χ2(1, N = 1.000) = 73,24, p < 0,001.
No entanto, o teste qui-quadrado não responde à pergunta “qual é a magnitude dessa associação?”. Neste caso, para respondê-la, precisamos recorrer à razão de chances.
Como calcular a razão de chances?
No contexto da razão de chances, queremos avaliar a chance de um participante relatar já ter visto OVNIs, dado que ele consome cogumelos mágicos, em comparação à chance de um participante relatar já ter visto OVNIs, dado que ele não consome cogumelos mágicos. Para tanto, seguiremos três passos para o cálculo:
Passo 1: Primeiramente, calcule a chance de um participante relatar já ter visto OVNIs, dado que ele consome cogumelos mágicos. Isto é, compute a razão A/C. Com base na Figura 2, essa chance é de 36/72 = 0,50.
Passo 2: Em seguida, calcule a chance de um participante relatar já ter visto OVNIs, dado que ele não consome cogumelos mágicos. Isto é, compute a razão B/D. Com base na Figura 2, essa chance é de 64/828 = 0,077.
Em outras palavras, os passos 1 e 2 sugerem que há mais chances de alguém relatar já ter visto OVNIs entre aqueles que consomem cogumelos mágicos do que entre aqueles que não os consomem. Mas quantas vezes mais chances? Essa resposta é dada pela razão de chances, calculada no último passo.
Passo 3: Finalmente, calcule a razão entre as duas chances anteriores para obter a razão de chances (RC). Ou seja, RC = 0,50/0,077 = 6,47. Esse valor indica que quem consome cogumelos mágicos tem 6,47 vezes mais chances de relatar já ter visto OVNIs em comparação a quem não consome tais cogumelos.
Como interpretar a razão de chances?
Os três passos descritos anteriormente podem ser sumarizados em uma única equação:
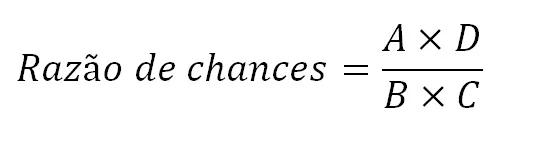
Com base no exemplo anterior, temos:
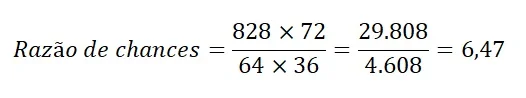
Cujo resultado é idêntico ao obtido no cálculo em três passos descrito na seção anterior.
A razão de chances complementa a informação do teste qui-quadrado de independência. Agora, além de sabermos que há uma associação significativa entre consumo de cogumelos e relatos de já ter visto OVNIs, podemos fazer uma afirmação acerca da magnitude dessa associação.
Para concluir esta seção, vamos sumarizar as três principais interpretações do valor da razão de chances:
- Razão de chances = 1: não há associação entre variáveis. Em outras palavras, as chances de ocorrência do evento são iguais entre condições ou grupos;
- Razão de chances > 1: isso ocorrerá quando o numerador tiver valor maior que o denominador. Desse modo, as chances do evento são maiores para o grupo ou condição no numerador;
- Razão de chances < 1: isso ocorrerá quando o denominador tiver valor maior que o numerador. Desse modo, as chances do evento são maiores para o grupo ou condição no denominador.
Observações importantes sobre a razão de chances
Neste ponto, duas observações importantes sobre a razão de chances merecem destaque.
Primeiramente, os valores da razão de chance variam desde valores muito próximos de zero (quando o numerador é pequeno e o denominador é grande) até valores que tendem ao infinito (quando o numerador é grande e o denominador é pequeno).
Quando o valor obtido é menor que 1, sua interpretação não é muito intuitiva. Desse modo, uma solução simples em tais situações é inverter numerador e denominador:

O novo valor reflete quantas vezes o evento é mais provável para o grupo ou condição no denominador, versus para o grupo ou condição no numerador.
Essa mesma lógica se aplica às chances. Por exemplo, anteriomente nós calculamos a chance de um participante relatar já ter visto OVNIs, dado que ele não consome cogumelos mágicos, 64/828 = 0,077. Se calcularmos 1/0,077 = 12,98, então concluíremos que há quase 13 vezes mais chance de quem não consome cogumelos mágicos não relatar já ter visto OVNIs, do que relatar já ter visto.
Em segundo lugar, para avaliarmos a razão de chances, é útil construirmos intervalos de confiança de 95% ao redor dessa estimativa. Se os intervalos não capturam o valor 1, então podemos inferir que há uma associação entre as variáveis.
Se os valores estiverem acima de 1, isso refletirá uma chance maior do evento para o grupo ou condição no numerador, enquanto se os valores estiverem abaixo de 1, isso refletirá uma chance maior do evento para o grupo ou condição no denominador.
Razão de chances em tabelas de contingência I × J
E quando eu tenho uma tabela de contingências maior? Em tais situações, não existe apenas uma única razão de chances que poderá ser calculada (Agresti, 2002, p. 54). Seja I o número de linhas de uma tabela e J, o número de colunas, então é possível calcular (I – 1)(J – 1) razões de chance.
Por exemplo, a Figura 3 apresenta uma tabela de contingências 2 × 4, representando quatro áreas de preferência de calouros e de veteranos de um curso de graduação qualquer. Com base nesses dados, podemos calcular (2 – 1)(4 – 1) = 3 razões de chance.
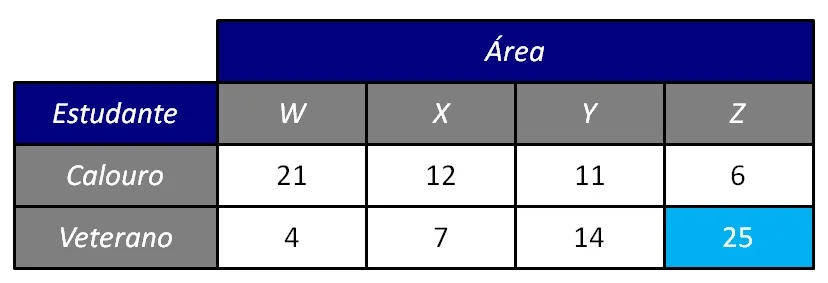
Note que a célula Veterano/Z está destacada em azul claro. Isso foi feito para indicar que selecionamos a linha Veterano e a coluna Z como referência, a partir da qual compararemos a linha Calouro e todas as demais colunas.
O cálculo das razões de chance é feito de maneira similar àquela apresentada anteriormente, exceto que “decompomos” a tabela original em três tabelas de contingência 2 × 2, desde que a linha e coluna que selecionamos como referência esteja presente em todas elas. A Figura 4 ilustra essa ideia.
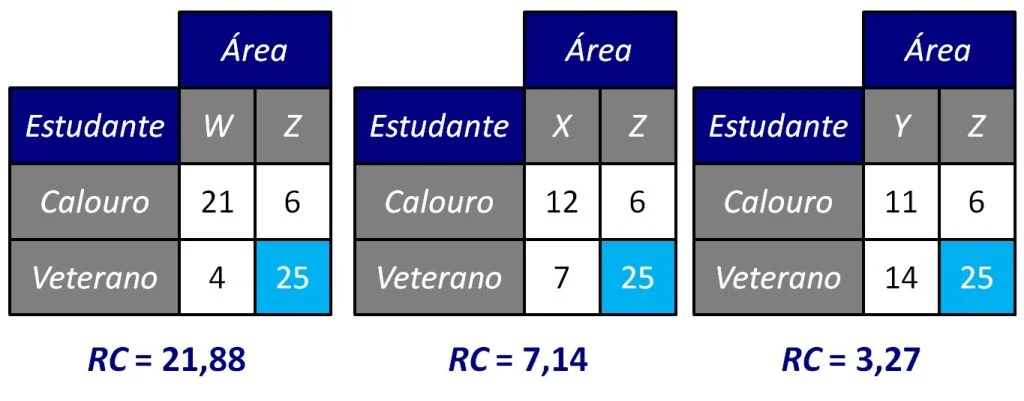
Podemos interpretar os resultados da Figura 4 da seguinte maneira: (a) painel esquerdo: calouros têm 21,88 mais chances de preferir a área W em relação à área Z do que veteranos; (b) painel central: calouros têm 7,14 mais chances de preferir a área X em relação à área Z do que veteranos; e (c) painel direito: calouros têm 3,27 mais chances de preferir a área Y à área Z do que veteranos.
Conclusão
Neste post, você aprendeu o que é razão de chances, como calculá-la e como interpretá-la. Você também aprendeu como interpretar a razão de chances no contexto de uma tabela de contingências 2 × 2, bem como sua extensão para tabelas de ordem superior.
Se você gostou desse conteúdo, então recomendamos que veja também nossos posts sobre o coeficiente φ (letra grega phi) e o V de Cramér, outras medidas de tamanho de efeito para testes de associação.
Precisa aprender análise de dados? Então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Agresti, A. (2002). Categorical data analysis (2nd ed.). John Wiley & Sons, Inc.
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Hair, J. F., Jr., Black, W. C., Babin, B. J., Anderson, R. E., & Tatham, R. L. (2009). Análise multivariada de dados (6ª ed.). Artmed.
Como citar este post
Lima, M. (2024, 24 de julho). Razão de chances (odds ratio): O que é, como calcular e como interpretar? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-e-razao-de-chances-odds-ratio













