A regressão linear múltipla é uma técnica estatística que usamos a fim de modelar a relação linear entre uma variável de desfecho contínua e múltiplas variáveis preditoras que podem ser contínuas ou categóricas.
A principal diferença entre as regressões lineares múltipla e simples é que, na simples, só usamos uma variável preditora. Por outro lado, na regressão linear múltipla, nós usamos duas ou mais variáveis preditoras.
Saiba mais: O que é regressão linear simples?

Quando usar regressão linear múltipla?
Podemos usar a regressão linear múltipla quando o objetivo da pesquisa envolve:
- Estimar o valor de uma variável de desfecho (também chamada de variável dependente, VD) por meio de um conjunto de variáveis preditoras (também chamadas de variáveis independentes, VIs).
- Investigar quais variáveis se relacionam com uma variável de desfecho.
- Investigar qual conjunto de variáveis traz uma melhor explicação para a variável de resultado.
- Entender a relação entre uma variável de resultado e uma preditora, controlando pelo efeito de outras variáveis preditoras.

A partir desses tipos de uso, podemos, portanto, pensar em alguns exemplos práticos:
- Estimar a nota de língua portuguesa em uma turma a partir da quantidade de exercícios de casa resolvidos, horas de estudo, número de faltas e quantidade de livros lidos no último ano.
- Identificar qual variável mais impacta a nota de língua portuguesa. Por exemplo, seriam os exercícios de casa, horas de estudo, número de faltas ou a quantidade de livros lidos no último bimestre? Desse modo, ao identificarmos a importância relativa dessas variáveis, podemos planejar uma intervenção educacional.
- Entender quais variáveis têm impacto sobre a qualidade de vida de um país a partir de um censo com dezenas de variáveis.
- Investigar se a quantidade de horas de aula matemática é uma boa variável preditora para a nota da prova de matemática, quando também observamos se os alunos fazem os exercícios em sala de aula.
O que preciso saber antes de fazer a regressão linear múltipla?
Anteriormente, nós já falamos sobre os pressupostos da regressão aqui e aqui. Uma vez que esse é um assunto muito importante, vale a pena relembrar que, antes de executarmos a regressão linear múltipla, nós devemos conferir se os dados seguem aos seguintes pressupostos:
- Linearidade: a relação entre a variável de desfecho e as variáveis preditoras deve ser linear.
- Homoscedasticidade (ou homogeneidade de variância): os termos de erro devem ter variância constante, ou seja, essa variância devem ser independente dos valores das variáveis preditoras. Quebramos esse pressuposto quando o termo de erro é maior ou menor a depender do nível da variável preditora.
- Independência de erros: os erros nas variáveis preditoras não devem estar correlacionados entre si.
- Ausência de multicolinearidade: as variáveis preditoras não podem ter multicolinearidade. Em outras palavras, se duas variáveis preditoras tiverem correlação muito alta, elas devem ser combinadas em uma única variável, ou então o pesquisador deverá selecionar apenas uma delas para inserir no modelo de regressão.
- Baixa exogeneidade: os valores das variáveis preditoras não devem estar contaminados com erros de medida. Contudo, ressaltamos que esse pressuposto não é muito realístico para a Psicometria. Ainda assim, é importante conhecê-lo. Erros de medida podem levar estimativas inconsistentes e superestimação dos coeficientes de regressão.
Entendendo a fórmula da regressão linear múltipla
Se você leu nossa postagem sobre regressão linear simples, você já deve saber que a fórmula da regressão nada mais é do que a equação que descreve uma reta:
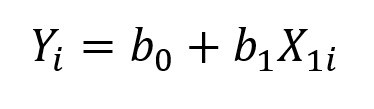
onde Y é a variável de resultado de interesse, isto é, a variável que queremos prever; X1 é nossa variável preditora; o subscrito i representa o caso i em nosso banco de dados; b0 é o intercepto do modelo, que representa o valor previsto de Y quando X = 0; e b1 é a inclinação da reta, que representa a mudança prevista em Y a partir da mudança em uma unidade de X. O b1 indica, portanto, o quão influente é a variável preditora.
Na regressão linear múltipla, por sua vez, temos uma fórmula bastante parecida. Em síntese, nela acrescentamos mais preditoras. Por exemplo, no caso em que temos duas variáveis preditoras, representamos nosso modelo da seguinte maneira:
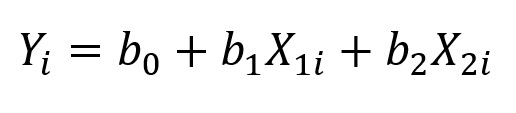
onde X2 é a segunda variável preditora de nosso modelo, com seu respectivo coeficiente associado, b2; os demais termos têm o mesmo significado da equação anterior.
O modelo de regressão linear múltipla com dois preditores pode se generalizar para a situação em que temos k variáveis preditoras:
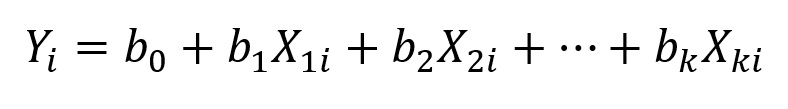
onde cada um dos preditores, X1, X2, …, Xk tem o seu respectivo coeficiente, b1, b2, …, bk associado.
O que é a regressão linear múltipla na prática?
Em seguida, vamos entender o que é a regressão linear através de um exemplo prático. Para isso, vamos dar continuidade ao nosso exemplo da regressão linear simples, onde analisamos se o escore de felicidade médio de um país tem relação com alguns indicadores.
No caso da regressão simples, analisamos se a felicidade tem relação com o Produto Interno Bruto (PIB) do país. No entanto, é possível estender esse modelo. Por exemplo, podemos acrescentar ao modelo de predição as variáveis liberdade para fazer escolhas de vida e suporte social.
Para termos uma base de comparação, em nosso modelo original, somente com o PIB, obtivemos R² de 0,63. Resumimos os índices de ajuste do nosso novo modelo na Tabela 1.
| Erro-padrão residual | 0,558 (gl = 152) | |
| R² múltiplo | 0,753 | |
| R² ajustado | 0,749 | |
| Estatística F | 154,9 (gls = 3 e 152) | p < 0,001 |
Como analisar as medidas de ajuste da regressão linear múltipla?
Podemos começar nossa análise checando se a regressão linear é um modelo diferente o suficiente do modelo nulo (que é a média da variável de interesse). O que nos dá esta informação é a estatística F. Se o valor de F for significativo, com p < 0,05, podemos dizer que a regressão linear é diferente do modelo nulo. No nosso exemplo, obtivemos valor de p menor do que 0,001, F(3, 152) = 154,9, p < 0,001.
Em um primeiro momento podemos pensar que o modelo ter um valor de p muito menor do que o necessário (0,001 << 0,05) é muito bom. Isto não é necessariamente verdade. O valor de p associado à estatística F apenas nos diz se o modelo é diferente do modelo nulo. Dito de outra forma, valores de p muito pequenos nos dizem que a chance dos modelos serem diferentes é grande. Entretanto, não diz o quão diferente eles são.
Avaliando a qualidade do modelo de regressão linear múltipla através do R²
Para avaliarmos a qualidade do modelo, podemos usar as medidas de R², que irá nos dizer qual é o percentual da variação dos dados pode ser explicada pelas variáveis preditoras. O R² do nosso modelo foi de 0,753. Isso significa que 75,3% da variação dos escores médios de felicidade pode ser explicada pelas variáveis preditoras, o que é excelente!
Apesar dos resultados impactantes, precisamos de cautela quando usamos o R² na regressão linear múltipla. O R² tem um viés: ele sempre aumenta conforme acrescentamos novas variáveis à regressão, ainda que estas variáveis sejam ruins enquanto preditoras. Desta maneira, é possível ter modelos com muitas variáveis ruins e um bom R². Para resolver este viés, existe uma outra estatística, o R² ajustado, que leva em conta que estamos acrescentando novas variáveis ao modelo. Em nosso caso, o R² ajustado é apenas ligeiramente menor que o R², 0,749 ou 74,9%, o que é um ótimo sinal!
O que é o erro-padrão residual?
Uma outra medida de ajuste presente é o erro-padrão residual. Ele indica o quão distante da linha de tendência da regressão estão os dados. Quanto menor o erro-padrão residual, melhor é nosso modelo. Porém, ele não é uma medida padronizada, seguindo o mesmo nível de medida da variável de interesse. Com isso, não há uma maneira padronizada de analisá-lo.
Outro ponto importante é que o R² é calculado à partir do erro-padrão residual. Portanto, ambas as medidas dão informações semelhantes.
Como saber se meu modelo de regressão linear múltipla tem boas variáveis preditoras?
Agora que sabemos que nosso modelo de regressão é adequado para os nossos dados, podemos voltar nossa atenção às variáveis preditoras. Sendo assim, da mesma maneira que fizemos ao analisar o modelo geral, a primeira coisa que vamos olhar são os valores de significância das variáveis, que também devem ser menores do que 0,05 (Tabela 2).
| b | β | Erro-padrão b | t | p | |
| Intercepto | 2,05 | 0,00 | 0,20 | 10,223 | < 0,001 |
| PIB | 1,28 | 0,46 | 0,17 | 7,44 | < 0,001 |
| Liberdade | 1,94 | 0,25 | 0,35 | 5,54 | < 0,001 |
| Suporte social | 1,19 | 0,32 | 0,24 | 5,02 | < 0,001 |
Em nossos exemplo, todos os coeficientes (bs) têm valores de p associados < 0,001. Em outras palavras, todas as variáveis preditoras contribuem significativamente para a predição da felicidade média em um país. O valor p é derivado da estatística t, que, por sua vez, corresponde à razão entre b e erro-padrão do b.
Da mesma maneira como fizemos para o ajuste do modelo, precisamos olhar o tamanho do impacto destas variáveis na variável de resultado. No caso das variáveis preditoras, existem duas medidas que podemos usar: os coeficientes não padronizados (bs) e os coeficientes padronizados (βs).
Como interpretar os valores dos coeficientes não padronizados?
Em síntese, o valor do coeficiente não padronizado (o b) determina o quanto a variável preditora impacta na variável de resultado. Isto é, quanto maior é o valor do módulo do b (ignorando seu sinal), mais influente ele é nos valores da variável de resultado.
Outra maneira de interpretar o b é que, na regressão linear múltipla, ele expressa a mudança esperada em Y, para a mudança em uma unidade da variável X a ele associado, controlando pelos efeitos dos demais preditores incluídos no modelo.
Por exemplo, nosso modelo de regressão estima que, se aumentássemos uma unidade no valor do PIB de um país, aumentaríamos em média 1,28 os escores de felicidade de um país (b = 1,28, t = 7,44, p < 0,001).
Quando usar os coeficientes padronizados?
Os bs da regressão sempre estão na mesma unidade de medida da variável original (e.g., os escores de felicidade que vão de 1 a 5). Consequentemente, pode ser difícil de identificar de maneira fácil o quão importante é aquela variável.
A fim de resolver este problema, podemos usar coeficientes padronizados, representados pela letra grega beta (β). Em síntese, o β é uma versão padronizada do b, que pode ser interpretado da seguinte maneira: o β indica qual é a mudança prevista na variável de resultado, em unidades de desvio-padrão, a partir da mudança em uma unidade de desvio-padrão da variável preditora — controlando pelos demais preditores inseridos no modelo.
Quando o β = 0, a relação entre as variáveis é fraca; em contrapartida, quando o beta é –1 ou +1, há uma relação forte entre as variáveis. Note que βs negativos, padronizados ou não, indicam que o aumento da variável preditora implica na diminuição da variável de resultado.
Em nosso exemplo, a variável mais influente para os escores médios de felicidade foi o PIB (β = 0,46), seguido por suporte social (β = 0,32) e a liberdade de escolhas de vida (β = 0,25).
Um ponto interessante para se notar é que quando fizemos a regressão linear simples, o PIB tinha β = 0,79; no entanto, agora seu valor caiu para 0,46.
Esta diminuição acontece pois há uma sobreposição entre o PIB, a liberdade de escolha e o suporte social. Apenas para fins de ilustração, podemos pensar que países com maior PIB também têm maior suporte social. Sendo assim, uma parte do poder explicativo do PIB diminui quando acrescentamos o suporte social no modelo.
Esta noção de que o poder de uma variável se altera quando acrescentamos outras ao modelo voltará quando falarmos de mediação e moderação.
Devo excluir variáveis não significativas ou fracas?
Você pode querer excluir variáveis por serem fracas ou com valor de p > 0,05 a fim de obter um modelo mais enxuto e parcimonioso. Mas não necessariamente esta é a melhor coisa a se fazer.
Por exemplo, se na sua pesquisa você tem um modelo teórico que está sendo avaliado a partir da regressão, é importante deixar as variáveis fracas e insignificantes dentro modelo. Isso demonstra que nem todas as suas hipóteses foram confirmadas empiricamente e, portanto,, deve ser objeto de discussão em seu estudo. Além disso, a não exclusão de variáveis fornece a maior transparência possível quanto ao modelo originalmente concebido na pesquisa.
Por outro lado, se você estiver procurando um modelo que seja o melhor para prever determinada situação, excluir variáveis pode aumentar o poder preditivo. Contudo, no caso de pesquisas científicas, ainda é necessário manter os dois modelos quando possível, para maior transparência dos resultados.
Para além da regressão linear múltipla
Após a leitura deste post, você agora deve ter uma boa ideia de como interpretar uma regressão linear múltipla. Acreditamos que isso te dará uma grande capacidade de análise em diversas situações.
Agora, se quiser ir além, entender a regressão linear te abre portas para compreender diversos tipos de análises que tomam a regressão linear como base. Sendo assim, recomendamos outros posts de nosso blog, que abordam tópicos como mediação e moderação, análise fatorial exploratória, modelagem por equações estruturais, regressão logística e regressão de Poisson. Bons estudos!
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Como citar este post
Damásio, B. (2021, 2 de março). O que é regressão linear múltipla? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-e-regressao-linear-multipla/















Respostas de 6
Gostei da aula
Obrigado, José!
Equipe Psicometria Online.
Olá Bruno Figueiredo. Espero que esteja bem.
Parabenizo-o pela explicação referente à regressão linear múltipla. De forma simples e didática e mostrando as entrelinhas facilitou a minha interpretação sobre a questão. Sugiro que continue com tal metodologia a fim de atingir os interessados nas questões estatísticas mas que ao mesmo tempo necessitam de um embasamento. Realmente, muito obrigado!
Oi, Frank. Que bom que o conteúdo te ajudou. Agradecemos o feedback!
Equipe Psicometria Online.
Já havia buscado outros blogs e vídeos tentando entender como analisar o valor de beta e só consegui entender aqui. Muito obrigada mesmo!
Oi, Ana Carla. Que bom que conseguimos te ajudar a entender a interpretar os coeficientes. Agradecemos o feedback!
Equipe Psicometria Online.