A regressão linear simples é o modelo mais básico dentro da família das regressões lineares. Nesse tipo de análise, utilizamos apenas uma variável preditora (também chamada de variável independente) para explicar ou prever os valores de uma variável de resultado (também chamada de variável dependente).
Por outro lado, quando empregamos duas ou mais variáveis preditoras, denominamos nosso modelo de regressão linear múltipla.
Neste post, abordaremos apenas a versão simples da regressão linear, isto é, a que possui apenas uma variável preditora. Se você quer entender mais sobre a regressão linear múltipla, então consulte nosso post sobre o tema.
Para que serve a regressão linear simples?
Utilizamos a regressão linear simples para descrever a relação linear entre duas variáveis. Ou seja, ela nos permite entender como o valor de uma variável pode mudar em função da variação de outra. Por isso, é uma ferramenta bastante útil em diversas situações.
De forma geral, recorremos à regressão linear simples quando:
- Queremos prever o valor de uma variável com base no valor de outra;
- Buscamos entender se (e como) duas variáveis estão relacionadas entre si;
- Precisamos criar um modelo inicial, antes de partir para modelos mais complexos, como a regressão linear múltipla.
Para deixar tudo mais concreto, veja alguns exemplos de aplicação da técnica:
- Avaliar se as habilidades de leitura variam em função da idade cronológica;
- Investigar se a insônia é um preditor da depressão;
- Utilizar um modelo simples, como a previsão da depressão a partir da insônia, e, em seguida, adicionar novas variáveis preditoras para criar um modelo mais complexo, mas também com maior poder preditivo.

Entenda os pressupostos antes de fazer a regressão linear simples
A regressão linear simples só é confiável quando os dados atendem aos seguintes pressupostos estatísticos:
- Linearidade: a relação entre as variáveis deve ser linear. Em outras palavras, o efeito da variável preditora sobre a variável de resultado deve ser constante ao longo de toda a escala.
- Homocedasticidade (ou homogeneidade das variâncias): os erros (ou resíduos) devem ter variância constante, independentemente dos valores da variável preditora. Violamos esse pressuposto quando há mais (ou menos) erro em determinados níveis da variável preditora.
- Independência dos erros: os erros devem ser independentes entre si. Isso significa que o erro associado a uma observação não pode estar relacionado ao erro de outra.
- Ausência de multicolinearidade: as variáveis preditoras não devem apresentar correlação quase perfeita entre si. Embora esse ponto seja relevante em modelos com múltiplas preditoras, é importante tê-lo em mente para futuras extensões do modelo.
- Baixa endogeneidade: os valores das variáveis preditoras não devem estar contaminados por erros de medida. Apesar de ser um pressuposto difícil de alcançar na prática — especialmente em áreas como a Psicometria —, é importante lembrar que a presença de erro de medida nas preditoras pode gerar estimativas inconsistentes e superestimar os coeficientes de regressão.
Entendendo a fórmula da regressão linear simples
O coeficientes de uma regressão linear simples nada mais são do que uma equação da reta:
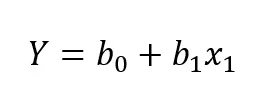
Onde Y se refere à variável de resultado (o que queremos prever) e x1 se refere à variável preditora (o que usamos para prever os valores da variável de resultado). A equação anterior expressa nossos coeficientes pela letra b. O b0, também chamado de intercepto, expressa o valor previsto para Y quando x1 = 0. O valor de b1, por sua vez, também chamado de inclinação da reta, expressa a força da relação linear entre as variáveis.
A Figura 1 apresenta um diagrama de dispersão relacionando duas variáveis quaisquer. Nela, cada ponto representa uma observação, com seus respectivos escores nas variáveis preditora e de resultado. Além disso, a linha pontilhada vermelha representa a reta que melhor descreve a relação entre as duas variáveis, onde x é a variável preditora, e Y é a variável de resultado.
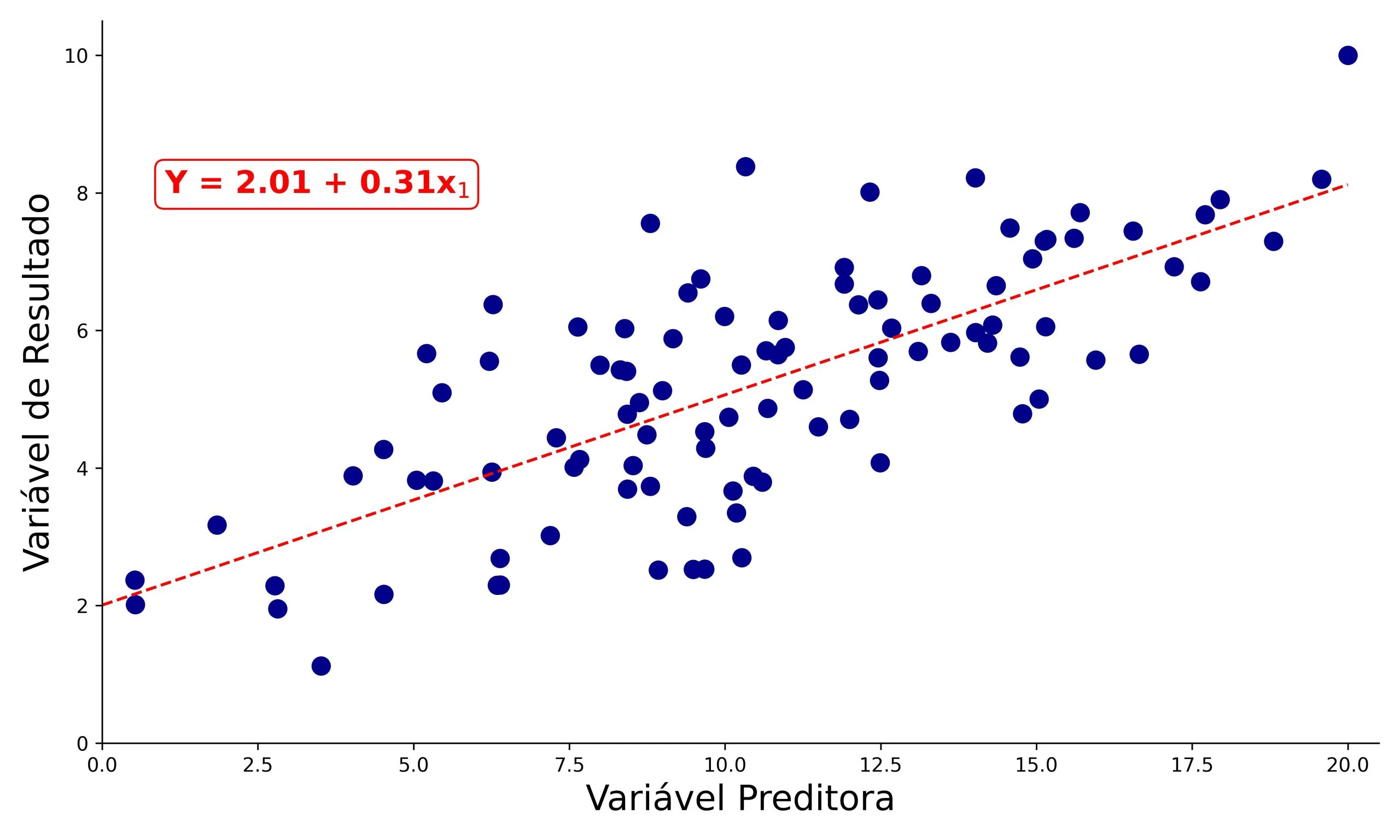
Para facilitar nossa interpretação, vamos assumir que, na Figura 1, a variável preditora representa o número de horas estudadas para um exame (entre 0 e 20 horas) e a variável de resultado, a nota obtida no exame (entre 0 e 10). Repare a seguir como os valores dos coeficientes (2,01 e 0,31) determinam a reta no gráfico da Figura 1.
A equação da reta de regressão sugere esperamos uma nota próxima a 2 por parte de um estudante que não estudou para o exame (b0 = 2,01), e um aumento na pontuação de 0,31, para cada hora adicional de estudo (b1 = 0,31).
Exemplo prático de regressão linear simples
Em seguida, mostraremos como conduzir e interpretar uma regressão linear simples. Para facilitar, usaremos os mesmos dados que usamos para criar a Figura 1. Sendo assim, nosso objetivo é prever a nota nos exames por parte dos estudantes, tomando como variável preditora o tempo que eles estudaram para o exame.
A Tabela 1 apresenta as estatísticas de ajuste do modelos de regressão linear simples aos dados.
| Soma dos quadrados | Graus de liberdade | Média quadrática | F | p | |
| Regressão | 165,237 | 1 | 165,237 | 113,395 | < 0,001 |
| Resíduos | 142,804 | 98 | 1,457 | ||
| Total | 308,042 | 99 |
A Tabela 2, por sua vez, apresenta os coeficientes de regressão que nos permitirão fazer interpretações sobre a relação entre variáveis.
| Variável | b | EP(b) | β | t | p |
| Intercepto | 2,01 | 0,33 | 6,17 | < 0,001 | |
| x1 | 0,31 | 0,03 | 0,73 | 10,65 | < 0,001 |
Agora que fomos formalmente apresentados aos resultados da regressão, vamos entender cada item das Tabelas 1 e 2.
Soma dos quadrados, graus de liberdade e média quadrática
De maneira simplificada, esses valores são cálculos intermediários usados para obtermos a estatística F e o R², sobre os quais falaremos adiante. Por exemplo, a soma dos quadrados total representa a variabilidade total dos valores de Y, ou seja, o erro quadrático que cometemos ao tentar prever Y usando a própria média de Y como preditora.
Na regressão linear simples, nosso objetivo é avaliar se o modelo baseado em x1 (a variável preditora) é melhor do que o modelo nulo, que usa a média de Y para predizer Y. Ou seja, queremos ver se as informações de x1 ajudam a explicar melhor Y do que simplesmente utilizar a média de Y como preditor.
Sendo assim, a soma dos quadrados de regressão representa a parte da variabilidade de Y explicada pelo nosso modelo (ou seja, o quanto o modelo melhora a previsão em relação ao uso da média de Y). Já a soma dos quadrados dos resíduos é o quanto o modelo ainda não consegue explicar, ou seja, a variabilidade não explicada pelas previsões do modelo.
Para calcular a estatística F, nós calculamos não usamos as somas dos quadrados diretamente. Ao invés disso, nós utilizamos os graus de liberdade (o número de valores que podem variar em uma análise, levando em consideração o número de parâmetros estimados no modelo), de modo a calcular médias quadráticas.
A média quadrática de regressão representa a variabilidade média de Y que o modelo de regressão explica, enquanto a média quadrática dos resíduos representa a variabilidade média de Y que o modelo de regressão não explica, ou seja, o erro do modelo.
A estatística F
Anteriormente, dissemos que nosso objetivo na regressão linear simples é examinar se nosso modelo de regressão é melhor que um modelo nulo — aquele que usa a própria média de Y para predizer Y. Em outras palavras, se nosso modelo de regressão não for significativamente superior que o modelo nulo, significa que ele é de pouca utilidade para pesquisadores.
Para essa avaliação, atentamo-nos para a estatística F, que consiste na razão entre a variabilidade média de Y explicada pelo modelo de regressão e a variabilidade média de Y não explicada pelo modelo de regressão. Matematicamente:
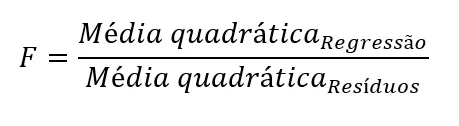
Usando os valores presentes na Tabela 1, temos F = 165,237 / 1,457 = 113,409, valor quase idêntico ao apresentado na Tabela 1 (F = 113,395) — pequenas diferenças no cálculo manual se devem a erros de arrendondamento.
Além disso, o software estatístico calcula o valor de p associado à estatística F obtida e aos graus de liberdade de regressão e dos resíduos. Se o valor de p for menor que nosso nível de significância (tipicamente, 0,05), concluímos que nosso modelo de regressão é estatisticamente melhor que o modelo nulo.
Em nosso exemplo, é exatamente isso que acontece. Poderíamos dizer, portanto, que nosso modelo de regressão foi estatisticamente melhor em explicar as notas dos estudantes no exame que o uso da própria média dos estudantes (modelo nulo), F(1, 98) = 113,40, p < 0,001.
O que é R²?
O coeficiente de determinação (R²) é uma medida que nos diz qual é a proporção (entre 0 e 1) da variância nos valores de Y que nosso modelo é capaz de explicar. Calculamos o R² da seguinte maneira:
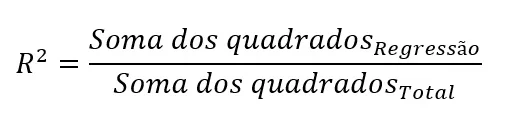
Usando os valores presentes na Tabela 1, temos R² = 165,237 / 308,042 = 0,536. Se multiplicarmos esse valor por 100, poderemos afirmar que nosso modelo de regressão explica, em sentido estatístico, 53,6% da variabilidade nas notas dos estudantes.
Ressaltamos que não existe uma maneira padronizada de quanto deve ser o valor de R². No entanto, devemos sempre interpretá-lo com base na teoria subjacente à relação hipotetizada entre nossas variáveis.
Para fins de exemplo, poderíamos considerar que 53,6% da variabilidade explicada nas notas com base no tempo de estudo para o exame. No entanto, isso também indica que os outros fatores explicam os 46,4% remanescentes da variabilidade em Y (tais como motivação, estratégias de estudo, autoeficácia etc.), os quais podem ser objetos de investigação em estudos subsequentes.
Saiba mais: Entenda o que é o coeficiente de determinação na regressão linear

O que preciso analisar no valor de p e na estatística t?
Em seguida, interpretaremos a Tabela 2. A primeira coisa que devemos olhar é se nossa variável preditora (x1 ou, em nosso exemplo, tempo de estudo) prediz significativamente as notas no exame.
A resposta a esse questionamento é dada pela estatística t e seu valor de p associado. Em síntese, a estatística t avalia se o valor de nosso coeficiente não padronizado (a coluna b, na Tabela 2) é estatisticamente diferente de 0. Se o valor de p for menor que nosso nível de significância (tipicamente, 0,05), então concluíremos que incluir a variável preditora melhora significativamente nosso modelo, em comparação ao modelo nulo.
Em nosso exemplo, a resposta é positiva: nossa variável preditora é uma variável que prediz significativamente os valores das notas dos estudantes no exame, t = 10,65, p < 0,001.
Obtemos o valor de p a partir da estatística t, na coluna ao lado da Tabela 2. Por isso, não é necessário analisar os valores brutos de t, mas é importante relatá-los, para que os resultados sejam transparentes.
Como interpretar os coeficientes não padronizados (bs)?
Antes de mais nada, as regressões lineares (simples e múltipla) geram tanto coeficientes não padronizados (bs) quanto coeficientes padronizados (betas ou βs).
Os valores dos coeficientes não padronizados (bs) são apresentados na Tabela 2, mas eles também já tinham aparecido na Figura 1. Em seguida, reapresentamos a Figura 1, mas agora com alguns detalhes adicionais.
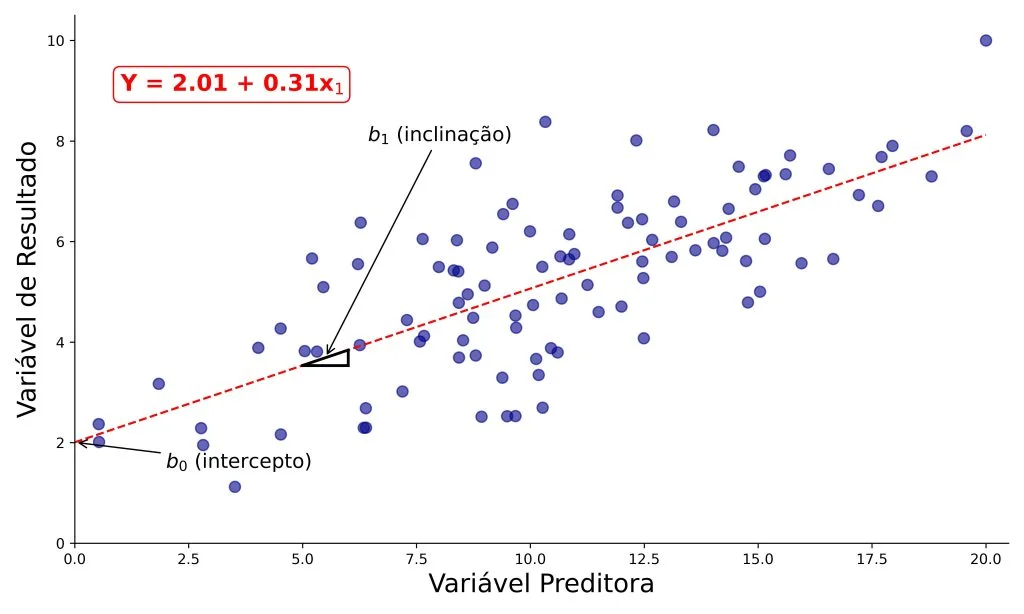
Em seguida, interpretaremos o intercepto e a inclinação da reta.
Como interpretar o intercepto?
Considere um estudante que simplesmente não estudou para a prova (x1 = 0). Para esse estudante, tomando como referência a equação da reta, teríamos:
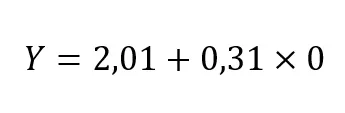
O que resulta em 2,01, isto é, o intercepto. Na Figura 2, o intercepto consiste no ponto do eixo Y por onde passa a reta de regressão. Sendo assim, o intercepto consiste no valor previsto para Y por nosso modelo de regressão quando x1 = 0.
Como interpretar a inclinação da reta?
Agora, considere um estudante que estude 5 horas para o exame. Calculamos o valor da nota prevista por nosso modelo da seguinte forma:
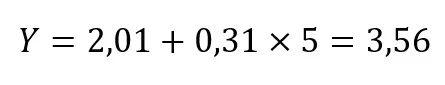
Segundo nosso modelo, o quanto a nota melhoraria se, ao invés de estudar 5 horas, um estudante estudasse uma hora a mais (i.e., 6 horas)? A nota prevista por nosso modelo por alguém que estude 6 horas é calculada a seguir:
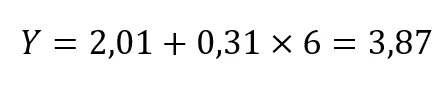
Não por um acaso, 6 horas – 5 horas = 1 hora, e nota 3,87 – nota 3,56 = nota 0,31. Logo, o coeficiente b1 = 0,31 representa a mudança prevista (aumento ou diminuição) na nota no exame em função da mudança em uma unidade (de estudo a mais ou a menos) na variável preditora.
Esse valor é representado pela altura do triângulo retângulo na Figura 2, sendo que, quanto mais alto for seu valor, mais íngreme será a inclinação da reta de regressão.
Como interpretar o coeficiente padronizado (β)?
Você pode se perguntar: mas o aumento de 0,31 na nota do exame em função de uma hora adicional de estudo é grande ou pequeno? Para termos uma interpretação mais fácil, podemos recorrer para o coeficiente padronizado (β) da Tabela 2.
Na regressão linear simples, o valor do β é idêntico ao de uma correlação. Sendo assim, se você já leu nosso artigo sobre correlação, você não terá dificuldades em interpretá-lo.
O β é dito um coeficiente padronizado porque seu valor é expresso em unidades de desvio-padrão, variando entre –1 e +1. Em síntese, o β expressa qual é a mudança esperada em Y, em desvios-padrões, dada a mudança em um desvio-padrão em x1. Valores próximos a zero indicam que há pouca ou nenhuma relação entre a varíavel preditora e a varíavel de resultado. Valores próximos a –1 e a +1 indicam que há uma relação forte entre as variáveis.
Em nosso exemplo, β = 0,73, o que é indicativo de uma relação forte entre o tempo de estudo para o exame a nota subsequente obtida nesse exame.
Erro-padrão
Nossa última métrica é o erro-padrão, que indica o quanto esperaríamos que de variabilidade no coeficiente não padronizado (b) caso repetíssemos o mesmo estudo várias vezes, com tamanhos amostrais iguais. Valores menores sugerem maior estabilidade, indicando que nosso coeficiente b tenderia a oscilar menos entre diferentes amostras.
Embora você não precise saber todos os detalhes técnicos, vale saber que o erro-padrão é utilizado tanto no teste de hipótese da significância do b (a estatística t nada mais é do que o valor de b dividido por seu erro-padrão), quanto no cálculo de intervalos de confiança (por exemplo, de 95%) ao redor de b.
Em ambos os casos, essas abordagens inferenciais nos permitem avaliar quais valores de b seriam implausíveis, e, portanto, poderiam ser rejeitados com base no valor empírico observado.
Uma observação sobre os coeficientes padronizados e não padronizados
Relembrando, nós definimos b como coeficiente não padronizado e β como coeficiente padronizado. No entanto, é importante que você saiba que a correspondência entre coeficientes não padronizados como bs e coeficientes padronizados como βs é uma convenção que nem sempre é seguida.
Sendo assim, recomendamos que você sempre explicite o significado de b e β em seus estudos, e que procure por essa informação quando ler os relatos de outros pesquisadores.
Regressão linear simples versus correlação de Pearson
Anteriormente, afirmamos que a regressão linear simples traz produz o mesmo valor (o coeficiente β) que o r de Pearson. Mas, se esse é o caso, qual das duas técnicas utilizar?
Se você estiver na dúvida, a regressão linear simples é mais adequada quando:
- O desenho da pesquisa envolve modelos de regressão linear múltipla, de modo que relatar uma regressão linear simples torna-se mais coerente do que apresentar apenas a correlação de Pearson;
- A regressão linear simples servirá como ponto de partida para a inclusão de outras variáveis no modelo;
- Você não está interessado nos coeficientes padronizados, mas deseja interpretar os resultados com base nos valores originais das variáveis;
- Você quer obter a equação da reta que descreve a relação entre as variáveis;
- Você está interessado em conhecer o valor do intercepto;
- Você deseja prever novos valores da variável de resultado, mas só possui os valores da variável preditora.
Por outro lado, a correlação de Pearson é mais simples de calcular e costuma ser mais adequada para a maioria dos casos em que não haverá inclusão de outras variáveis no modelo.
Conclusão
Após a leitura deste post, espero que você se sinta mais confiante para interpretar os resultados de uma regressão, compreendendo como analisar os coeficientes, as medidas de ajuste e o impacto da variável preditora sobre a variável de resultado.
Você também já está pronto para o próximo passo: a regressão linear múltipla, que nada mais é do que uma extensão da regressão linear simples, com a inclusão de múltiplas variáveis preditoras no modelo.
Gostou desse conteúdo? Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referência
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Como citar este post
Damásio, B. (2021, 14 de novembro). O que é regressão linear simples? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-e-regressao-linear-simples/














