O que são graus de liberdade?

O conceito de graus de liberdade está presente em diferentes contextos da análise quantitativa de dados. Por exemplo, os graus de liberdade aparecem entre parênteses nos relatos de artigos científicos, quando são reportados resultados de testes t, análises de variância e testes qui-quadrado.

Além disso, os graus de liberdade também estão presentes nas literaturas de análise fatorial confirmatória e de modelagem por equações estruturais, quando se discute a questão da identificabilidade de modelos.

Neste post, explicaremos o conceito estatístico de graus de liberdade. Além disso, você também aprenderá como o conceito aparece no dia a dia de pesquisadores quantitativos.

Qual é a definição de graus de liberdade?

Definição de graus de liberdade

Em estatística, os graus de liberdade (representado por gl, ou df, em inglês) consistem em uma medida que nos ajuda a determinar o número de observações que podem variar independentemente entre si no cálculo de uma estatística de interesse. Em outras palavras, eles indicam qual é o máximo que os valores podem variar para que nossas estatísticas ainda sejam válidas.

Os graus de liberdade são calculados como a diferença entre o número de observações, N, e o número de parâmetros que estamos estimando, k. Isto é, gl = N – k. Por exemplo, considere a seguinte igualdade:

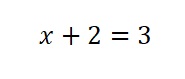
Nesse exemplo, temos duas observações (i.e., os valores 2 e 3) e uma incógnita (i.e., o x). Essa incógnita pode ser pensada como o “parâmetro” que queremos estimar. Nesse caso, é simples identificarmos o valor que torna a igualdade verdadeira: x = 1.

Aqui é importante destacar que só fomos capazes de obter uma solução única para nossa equação porque tínhamos mais valores obervados que valores a serem estimados. Por outro lado, veja o que acontece neste cenário:

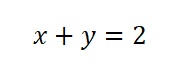
No novo exemplo, nosso conjunto solução contém infinitos pares que satisfazem a equação. Dois exemplos são x = 1, y = 1 e x = 0, y = 2, mas você facilmente pode identificar outros pares. Na linguagem da modelagem estatística, diríamos que essa equação representa um modelo não identificável, pois somos incapazes de encontrar uma solução única para a equação.

Graus de liberdade na modelagem por equações estruturais

No contexto da modelagem por equações estruturais, pesquisadores estimam parâmetros de múltiplas equações simultaneamente. O ponto importante aqui é que um modelo é: (a) identificável: quando sua especificação implica graus de liberdade positivos; ou (b) não identificável: quando a especificação implica graus de liberdade negativos.

Por exemplo, a Figura 1 apresenta um modelo de análise fatorial confirmatória que busca explicar a variância na resposta de dois itens por meio de um fator comum.

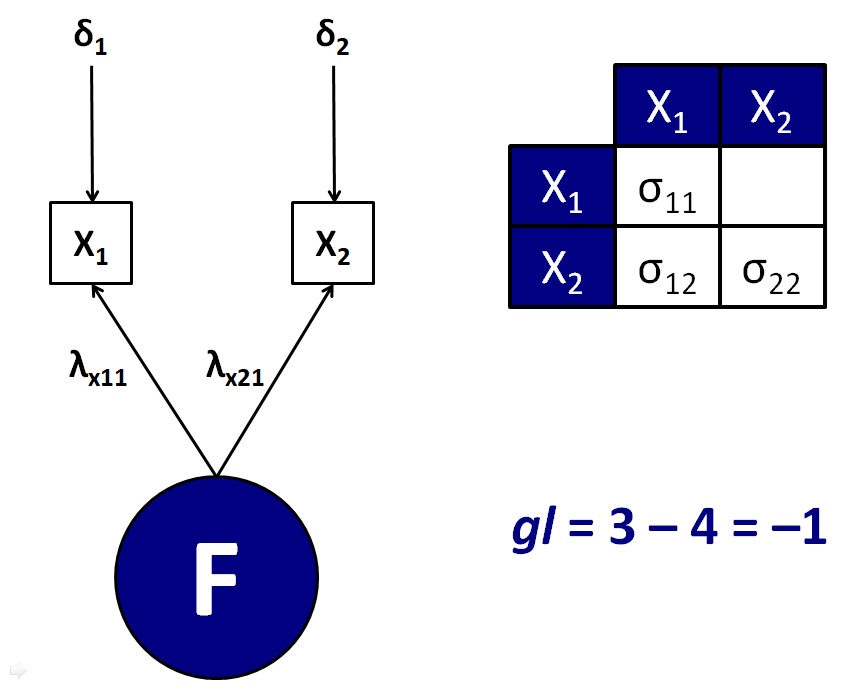
Como podemos ver, esse é um modelo não identificável, pois temos menos valores observados (as variâncias, σ₁₁ e σ₂₂; e a covariância, σ₁₂) que parâmetros no modelo (as cargas fatoriais, λ_X11 e λ_X12; e os resíduos, δ₁ e δ₂).

Veja também:

Um exemplo simples de graus de liberdade

Para melhorar nossa compreensão, vamos pensar em um exemplo simples. Uma avó presentou cada um de seus dois netos com um cartão de presentes no valor de 100 reais. No entanto, ela disse que eles poderiam realizar apenas três compras em um aplicativo de entrega de alimentos durante o fim de semana.

Assim sendo, cada neto seria responsável por administrar o valor de seu cartão de presentes da maneira que julgasse mais conveniente. No entanto, o uso dos recursos deveria ser feito com sabedoria.

Suponha que o neto A gastou 50 reais na primeira compra e 30 na segunda. Desse modo, sua terceira compra não pode ultrapassar 20 reais. Já o neto B gastou 10 reais na primeira compra e 15 na segunda. Desse modo, ele ainda poderá usar 75 reais em sua compra final. A Figura 2 ilustra esses cenários.

Apesar de a avó ter dado liberdade aos netos para escolher como gastar seus cartões de presentes, essa liberdade tem limites! A Figura 2 indica, portanto, que esses limites são determinados pelos gastos das duas primeiras compras. Embora os netos tenham liberdade, a terceira compra terá uma liberdade restringida pelos gastos anteriores.

Esse exemplo oferece uma metáfora do significado de graus de liberdade. Em seguida, forneceremos dois exemplos adicionais de como esse conceito aparece em testes de significância da hipótese nula.

Graus de liberdade em testes estatísticos

Teste t para grupos independentes

Eis um exemplo. Três argentinos e três brasileiros foram questionados sobre o quanto eles gostam de futebol, em uma escala de 0 (Detesto futebol) a 10 (Amo futebol).

A Figura 3 apresenta as médias de cada grupo. Esse é um cenário onde pesquisadores podem analisar seus dados usando o teste t para grupos independentes. A pergunta de pesquisa aqui é: “há diferenças nas médias das respostas de argentinos e brasileiros?”

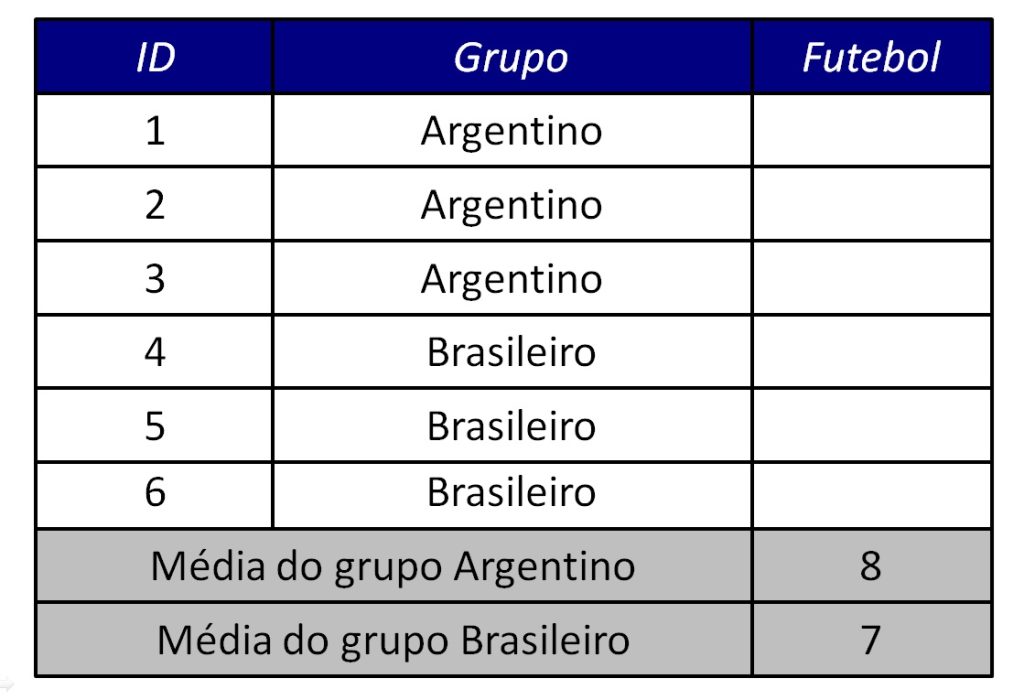
Reflita: qual é o número máximo de valores que podemos inserir livremente na tabela? Em outras palavras, quantos valores conseguimos inserir na tabela até que os valores omitidos fiquem determinados pelos valores já conhecidos?

Resposta: podemos preencher no máximo quatro valores da tabela (dois para argentinos e dois para brasileiros), antes que os outros sejam determinados pelas médias. A Figura 4 ilustra um possível preenchimento de quatro valores.

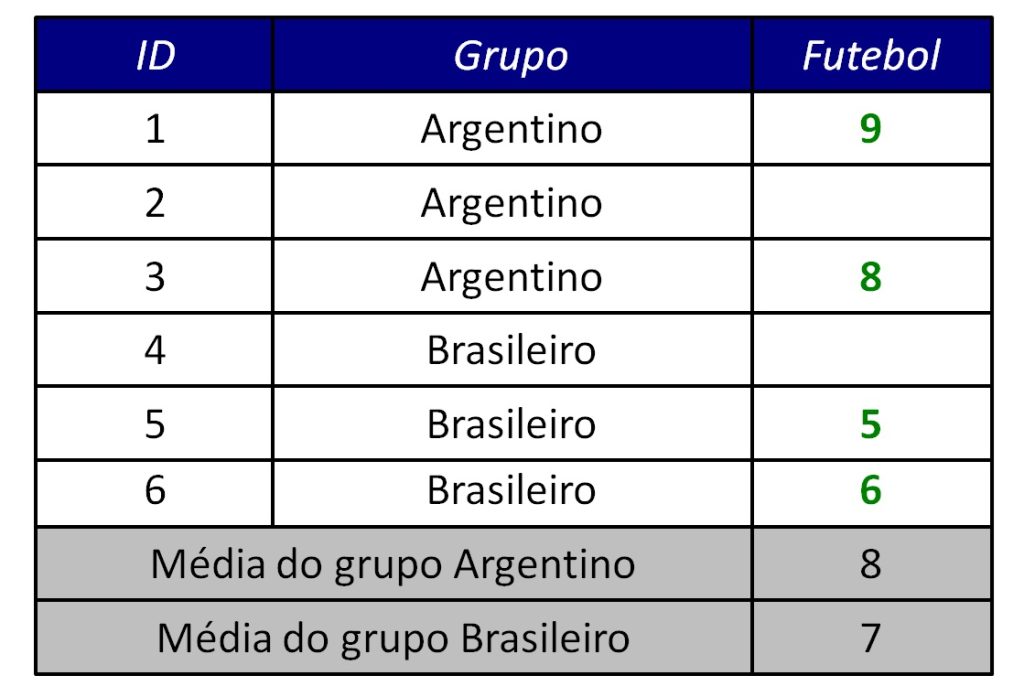
Sabendo que a soma das respostas dos dois primeiros argentinos é 17, a resposta do último argentino deve ser 7 para que a média seja, de fato, 8. O mesmo ocorre com os brasileiros: com soma 11, a resposta do último brasileiro deve ser 10 para que a média seja, de fato, 7.

A Figura 5 mostra a tabela completamente preenchida. Os valores em verde indicam as nossas escolhas arbitrárias. Temos 4 graus de liberdade ao preencher a tabela, dadas as médias. Uma vez preenchidos quatro valores, os demais (em vermelho) estarão determinados pelas médias.

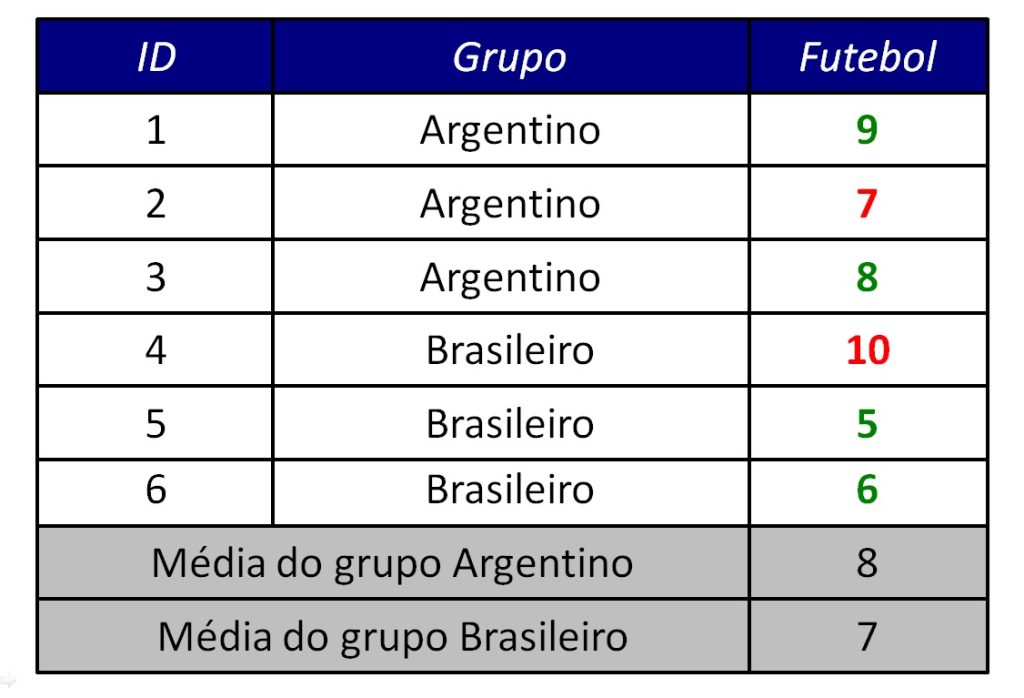
Nesse exemplo, N = 6 e k = 2 (no teste t, o k se refere às duas médias). Portanto, gl = 6 – 2 = 4, como mostrado no exemplo.

Teste qui-quadrado de independência

Considere que pesquisadores recrutaram participantes para reportar nacionalidade e esporte preferido. A Figura 6 mostra uma tabela de contingência 3 × 2, cruzando essas duas variáveis.

Os números de participantes em cada cruzamento das variáveis foram omitidos, mostrando apenas os totais marginais (somas das linhas ou colunas). Suponha que esses totais são fixos, mas o padrão de respostas ainda não é conhecido.

Pergunta: quantos valores podemos inserir livremente nas células da tabela antes que os totais marginais determinem os valores restantes?

Resposta: podemos preencher no máximo duas células (uma em cada coluna, desde que em linhas distintas). Após isso, os valores restantes são determinados pelos totais marginais. A Figura 7 ilustra um preenchimento possível de dois valores.

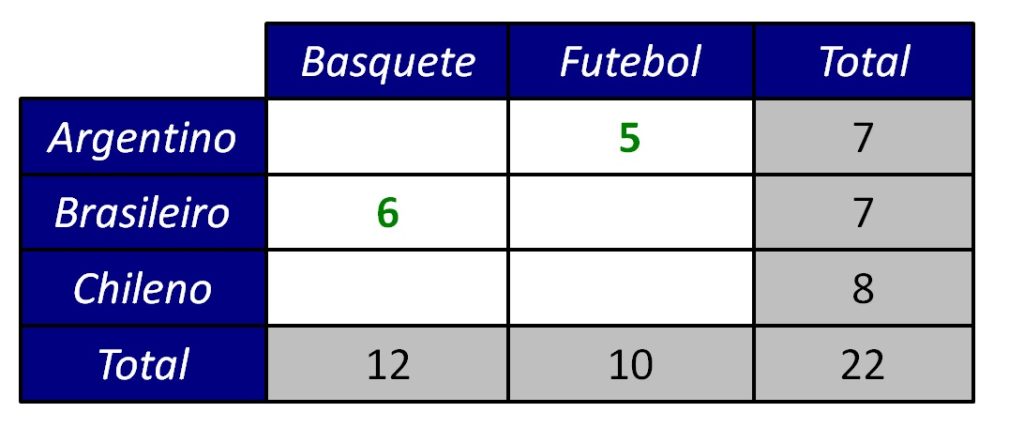
Se 5 de 7 argentinos preferem futebol, então os 2 restantes preferem basquete. Se 6 de 7 brasileiros preferem basquete, então o caso remanescente prefere futebol. Logo, 8 de 12 que preferem basquete não são chilenos; portanto, os outros 4 são chilenos. Assim, se 4 de 8 chilenos preferem basquete, os outros 4 preferem futebol.

A Figura 8 mostra a tabela de contingência totalmente preenchida. Células verdes foram preenchidas livremente (com dois graus de liberdade), e as vermelhas foram determinadas por esses valores e pelos totais marginais.

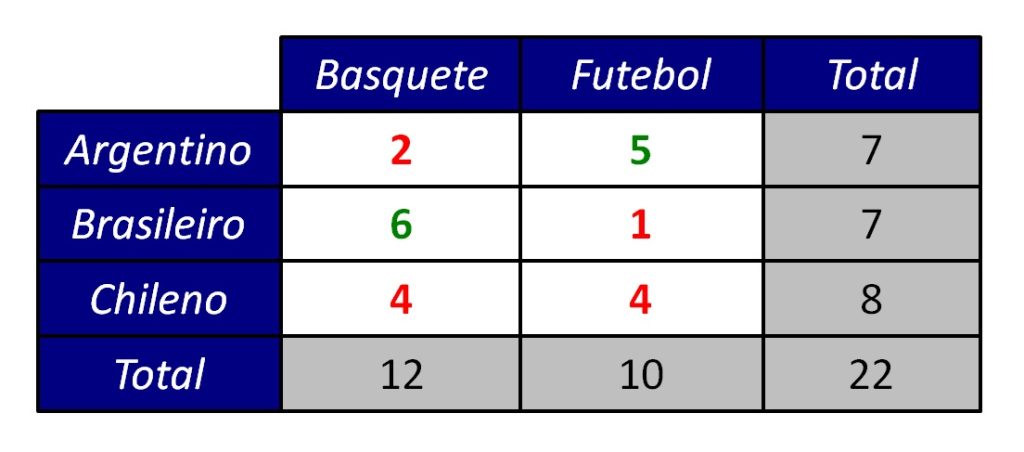
Conclusão: em uma tabela de contingência 3 × 2, temos apenas 2 graus de liberdade para preenchê-la. Seja m o número de linhas e n, o número de colunas da tabela. No teste qui-quadrado, nossos graus de liberdade são:

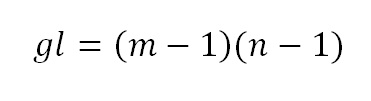
Em nosso exemplo, gl = (3 – 1)(2 – 1) = 2, como demonstrado anteriormente.

Qual é a importância dos graus de liberdade em estatística?

Os exemplos das seções anteriores ilustraram didaticamente a ideia de que graus de liberdade consistem no número de observações que podem variar independentemente entre si no cálculo de uma estatística de interesse. Mas qual é a importância dos graus de liberdade em estatística?

Nos testes de significância da hipótese nula, primeiro definimos uma hipótese nula, depois conduzimos um teste estatístico e, finalmente, comparamos a estatística do teste com o valor crítico de uma distribuição de probabilidade. Em geral, esse valor crítico está associado à cauda que contém os 5% (ou 2,5% em cada uma das caudas, em testes bicaudais) valores mais extremos da distribuição. Essa comparação determina, portanto, se rejeitaremos ou não a hipótese nula.

De particular importância, os graus de liberdade determinam a forma da distribuição de probabilidade contra a qual comparamos a estatística do teste de nossa amostra. Em seguida, ilustraremos essa ideia com as distribuições t e de qui-quadrado.

Distribuição t sob diferentes graus de liberdade

Lembrando, o teste t para grupos independentes compara as médias de dois grupos. A Figura 9 apresenta três distribuições ts, associadas a 4, 18 e 48 graus de liberdade.

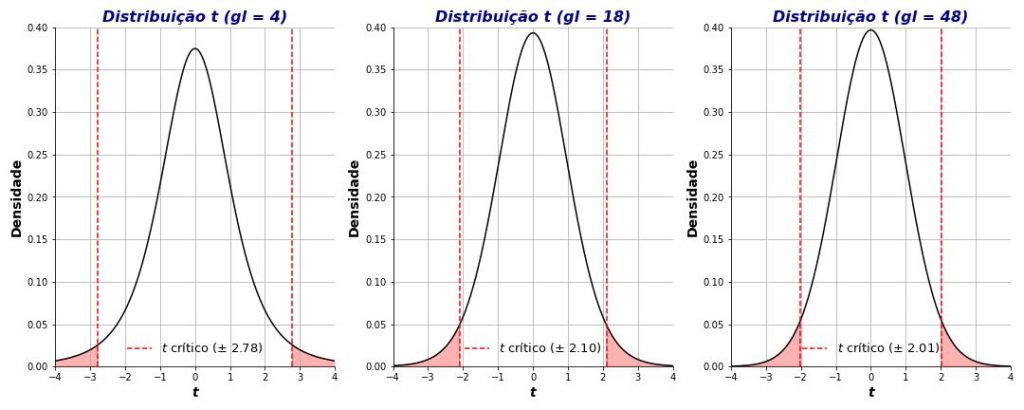
Você pode pensar nessas três distribuições, portanto, como diferentes representações da hipótese nula. O painel esquerdo representa a distribuição t sob a hipótese nula de que não há diferença entre dois grupos, totalizando 6 participantes, tal como em nosso exemplo de argentinos e brasileiros respondendo o quanto gostam de futebol. Os demais painéis representam hipóteses nulas similares, mas para estudos com 20 (gl = 18) e com 50 (gl = 48) participantes.

Mantidos outros fatores constantes, no teste t, quanto menores forem os graus de liberdade, maiores serão os valores críticos associados a um teste de significância da hipótese nula. Isso quer dizer que, em nosso exemplo sobre futebol, nosso teste t deveria produzir uma estatística t ≥ |±2,78| para que nosso valor de p fosse menor que 0,05.

À medida que os graus de liberdade aumentam, nossa hipótese nula passa a ser representada por caudas cada vez menos pesadas. Portanto, com gl = 18, uma diferença significativa passará a estar associada a um t crítico de |±2,10|, e esse valor diminuirá para t ≥ |±2,01|, quando gl = 48.

Se os graus de liberdade aumentarem ainda mais, a distribuição t se aproximará da distribuição normal, com valores críticos de t se aproximando de 1,96, tal como ocorre com o escore z na curva normal-padrão.

Distribuição de qui-quadrado sob diferentes graus de liberdade

A Figura 10 apresenta três distribuições de qui-quadrado, associadas a 1, 2 e 4 graus de liberdade. Em contrapartida ao que ocorre com os valores t críticos, no teste qui-quadrado de independência, quanto maiores são os graus de liberdade, maiores serão os valores qui-quadrados críticos que permitirão que pesquisadores rejeitem a hipótese nula de não associação entre variáveis.

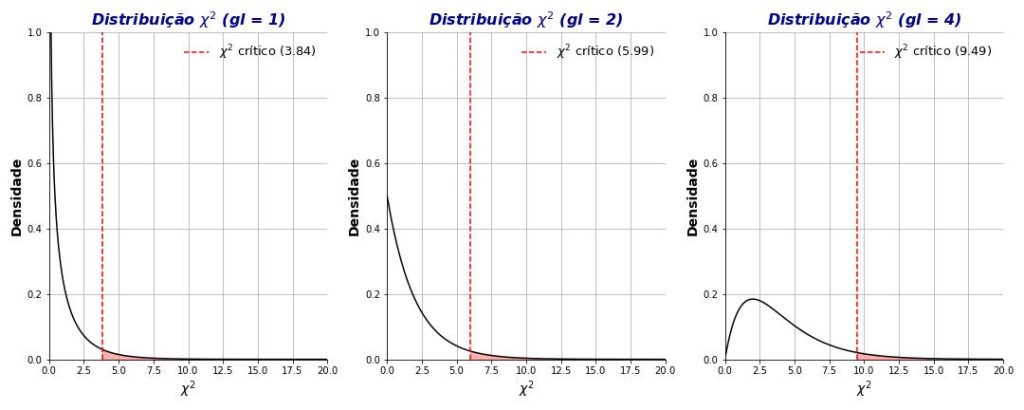
O painel central da Figura 10 pode ser pensado como representando a distribuição de qui-quadrado para a hipótese nula de não associação entre nacionalidade (argentino, brasileiro, chileno) e esporte preferido (basquete, futebol). Se a estatística de nosso teste produzisse um χ² ≥ 3,84, então rejeitaríamos essa hipótese nula.

O painel esquerdo representaria um delineamento similar, mas que tivesse, por exemplo, apenas duas nacionalidades, isto é, as duas variáveis categóricas com apenas dois níveis. Nesse caso, como m = 2 e n = 2, teríamos que gl = (2 – 1)(2– 1) = 1.

O painel à direita, por sua vez, representaria um delineamento com duas variáveis com três níveis cada como, por exemplo, com três nacionalidades e três esportes preferidos. Nesse caso, como m = 3 e n = 3, teríamos que gl = (3 – 1)(3 – 1) = 4.

Em síntese, os graus de liberdade são importantes porque eles determinam a forma da distribuição que representa a hipótese nula em um dado contexto de pesquisa. Na prática, contudo, os softwares estatísticos produzem automaticamente os valores da estatística do teste, graus de liberdade e valor de p, de modo que você não precisa se preocupar em como os cálculos são feitos.

O que é importante, no caso, é relatar adequadamente as estatísticas para o leitor. Para mais informações, consulte as orientações da American Psychological Association ou as diretrizes de sua área de pesquisa.

Conclusão

Neste post, você aprendeu um pouco mais sobre o conceito de graus de liberdade. Você viu que, em análise fatorial confirmatória e em modelagem por equações estruturais, queremos especificar modelos identificáveis, isto é, que possuem mais valores observados (e.g., variâncias, covariâncias) que valores a serem livremente estimados (e.g., cargas fatoriais, variâncias residuais, covariâncias entre erros).

No caso de testes estatísticos, os graus de liberdade são importantes porque eles determinam a forma da distribuição que representa a hipótese nula em um dado contexto de pesquisa. Se a forma a distribuição se altera a depender dos graus de liberdade do teste estatístico, então o valor crítico contra o qual compararemos a estatística do teste em nossa amostra também será diferente.

Gostou desse conteúdo? Então aproveite e também se inscreva em nosso canal do YouTube para ficar por dentro de nossos conteúdos por lá!

Precisa aprender análise de dados? Então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).

Referências

Brown, T. A. (2015). Introduction to CFA. In T. A. Brown, Confirmatory factor analysis for applied research (2^nd ed., pp. 35–87). The Guilford Press.

Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5^th ed.). Sage.

Walker, H. M. (1940). Degrees of freedom. Journal of Educational Psychology, 31(4), 253–269. https://doi.org/10.1037/h0054588

Como citar este post

Lima, M. (2021, 12 de agosto). O que são graus de liberdade? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-sao-graus-de-liberdade/