Ao planejar projetos de pesquisa quantitativa, pesquisadores devem sempre considerar o poder estatístico almejado. Essa etapa é essencial porque direciona as decisões sobre o delineamento do estudo, garantindo que os resultados obtidos sejam realmente informativos e confiáveis.
Neste post, explicaremos o que é o poder estatístico e por que ele é tão importante para o sucesso de um projeto de pesquisa. Além disso, vamos apresentar os principais fatores que influenciam o poder estatístico e esclarecer a diferença entre o poder estatístico clássico e o poder observado. Embora os dois conceitos pareçam similares, você verá que o poder observado não possui utilidade prática.
O que é poder estatístico?
O poder estatístico consiste na probabilidade de rejeitar a hipótese nula quando ela é realmente falsa. Em seguida, visando fornecer uma compreensão mais abrangente desse conceito, exploraremos alguns conceitos relacionados.

O que é teste de significância da hipótese nula?
No teste de significância da hipótese nula, a hipótese nula é a suposição que queremos testar e, potencialmente, rejeitar. Por exemplo, no tribunal do júri, o suspeito por um crime pode ser culpado ou inocente, e o papel do júri é dar um veredicto de “culpado” ou “não culpado” com base nas evidências apresentadas no tribunal.
Neste caso, a hipótese nula equivale à suposição de que o suspeito é inocente. Se as evidências forem fortes o bastante, o júri deve declarar o suspeito “culpado”. Caso contrário, o júri deve declará-lo “não culpado”. A Figura 1 representa as diferentes possibilidades de resultado de um julgamento.

Considerando apenas os casos em que o suspeito realmente cometeu o crime (Sim), o poder estatístico é análogo à probabilidade de o júri, com base nas evidências, declarar corretamente o suspeito culpado. Por outro lado, a probabilidade de o júri falhar em emitir esse veredicto correto, mesmo quando o suspeito é culpado, é análoga ao erro Tipo II.
Em um cenário ideal, o objetivo é ter um poder estatístico alto. Com isso, o erro Tipo II seria bastante raro. Em outras palavras, um poder estatístico elevado reduz o risco de falsos negativos, isto é, de declarar um criminoso como “Não culpado”.
Em termos práticos, considera-se que um estudo científico tem um poder estatístico adequado quando o valor atinge pelo menos 0,80. No exemplo do julgamento, isso significaria que o júri emite o veredicto de culpado corretamente em 80% dos casos. Dessa forma, os resultados se tornam mais confiáveis, minimizando, portanto, as chances de erro.
Poder estatístico, hipótese nula e hipótese alternativa
Agora, vamos deixar nossa metáfora de lado e retornar ao mundo da pesquisa científica. Relembrando, o poder estatístico é a probabilidade de rejeitarmos uma hipótese nula falsa. Especificamente, em pesquisas científicas, um poder de 0,80 indica que a probabilidade de detectar um efeito ou uma relação entre variáveis, caso esse efeito ou relação realmente exista, é de 80%.
Por exemplo, suponha que queremos avaliar se existem diferenças nos níveis de curiosidade de cães e gatos (conforme aferido por alguma medida com boas propriedades psicométricas). Supondo que os grupos sejam comparados por meio de um teste t para amostras independentes, teríamos as seguintes hipóteses:
- Hipótese nula (H0): os níveis médios de curiosidade não diferem entre cães e gatos.
- Hipótese alternativa (H1): os níveis médios de curiosidade diferem entre cães e gatos.
No que se refere à hipótese alternativa, adotamos uma hipótese bicaudal, isto é, que considera que cães podem ser mais curiosos gatos, ou que gatos podem ser mais curiosos que cães. Isso se opõe a uma hipótese alternativa unicaudal, que consideraria a hipótese nula implausível apenas se os níveis de curiosidade dos animais diferissem em uma direção pré-definida pelo pesquisador.
Poder estatístico e erros Tipos I e II
A Figura 2 apresenta esquematicamente o conceito de poder estatístico, juntamente com outros conceitos importantes relacionados ao teste de significância da hipótese nula.
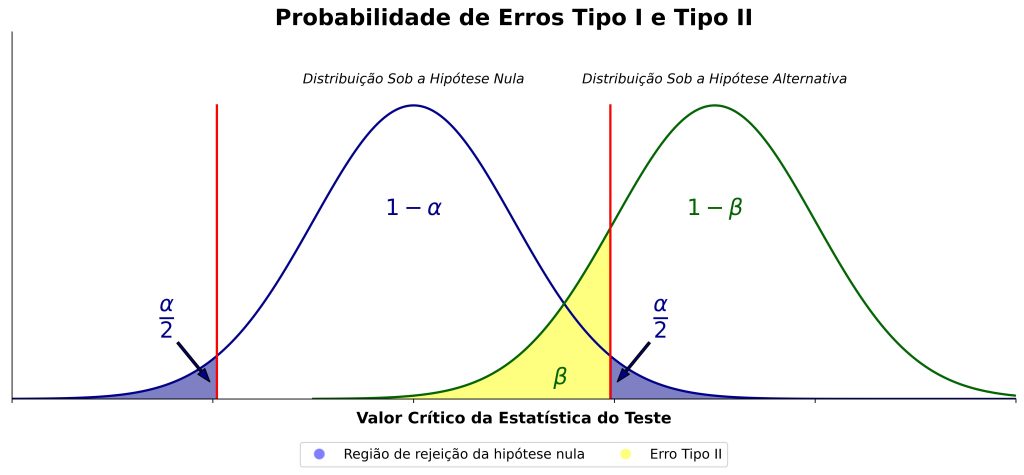
As regiões azuis da Figura 2 podem ser pensadas como “zonas de significância”, isto é, regiões cujos valores da estatística do teste t levariam à rejeição da hipótese nula. Por outro lado, a região amarela indica a probabilidade de erro Tipo II. Por fim, a região rotulada como “1 – β” representa o poder estatístico.
O poder estatístico nos informa sobre a probabilidade de observarmos um efeito estatisticamente significativo, considerando nosso tamanho amostral, nível de significância e o tamanho de efeito hipotetizado. Portanto, note que o poder estatístico é um conceito relacional: um mesmo tamanho amostral pode ter um poder estatístico adequado para detectar efeitos muito grandes, enquanto pode ter pouco poder estatístico para detectar efeitos menores.
Quais fatores influenciam o poder estatístico?
O poder estatístico é influenciado por quatro fatores principais, a saber, o nível de significância, o tamanho de efeito, a variabilidade na população-alvo e o tamanho amostral.
Nível de significância
Primeiramente, o poder estatístico diminui quando diminuimos o nível de significância. Por exemplo, os paineis da Figura 3 são idênticos, exceto pela posição das linhas verticais vermelhas. Em outras palavras, temos um nível de significância mais liberal no painel superior (α = 0,05), enquanto um critério mais conservador é apresentado no painel inferior (α = 0,01).
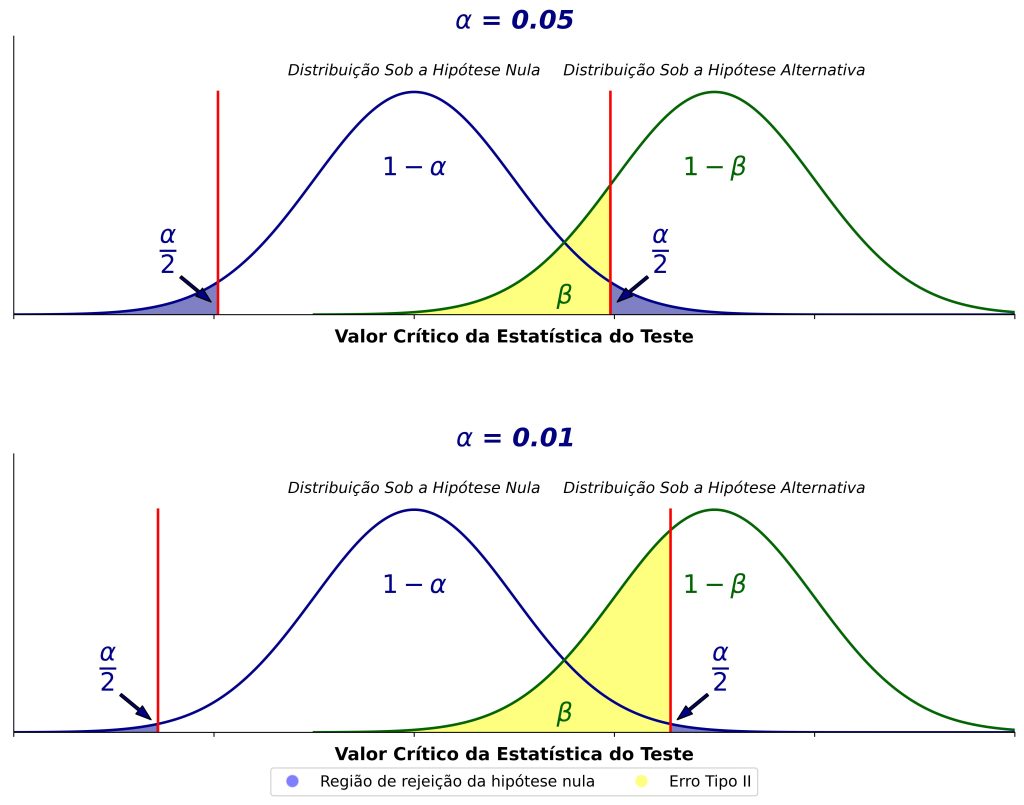
Como podemos ver na Figura 3, se diminuímos o nível de significância, estaremos sendo mais conservadores para rejeitar a hipótese nula (as regiões de rejeição ficarão menores), diminuindo assim a probabilidade de erro Tipo I. Em contrapartida, isso aumentará a probabilidade de erro Tipo II (região amarela maior) e, consequemtente, diminuirá o poder estatístico (região rotulada como “1 – β” menor).
Tamanho de efeito
Em segundo lugar, como mencionamos anteriormente, o poder estatístico é sempre considerado em relação a um tamanho de efeito a ser detectado. Em particular, o poder estatístico aumenta quando aumentamos o tamanho de efeito. A Figura 4 ilustra essa ideia.
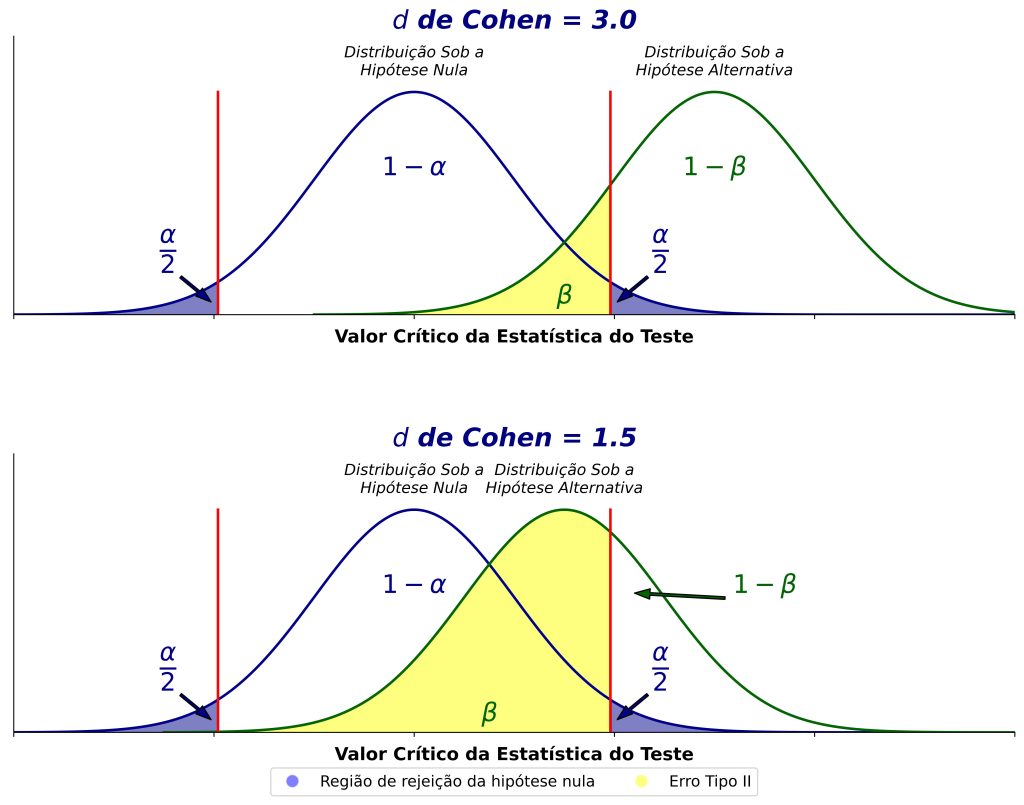
Quando o tamanho de efeito é menor (Figura 4, painel inferior), há mais sobreposição entre as distribuições sob as hipóteses nula e alternativa. Em outras palavras, podemos pensar no tamanho de efeito como “o grau de falsidade da hipótese nula” (muito falsa no painel superior, mas um pouco menos falsa no painel inferior). Concluímos, portanto, que mantendo outros fatores constantes, efeitos menores são mais difíceis de detectar (observe os tamanhos das regiões rotuladas como “1 – β” nos dois paineis).
Variabilidade na população-alvo
Além disso, a variabilidade na população-alvo também afeta o poder estatístico. Note que o termo população pode se referir a uma população genuína (e.g., residentes no Mato Grosso) ou a uma população hipotética criada artificialmente por meio de uma intervenção (e.g., indivíduos com transtornos de ansiedade que recebem 20 sessões de tratamento em terapia cognitivo-comportamental).
Se as populações são mais homogêneas, a tendência é que haja menor variabilidade amostral de estudo para estudo, o que aumenta a probabilidade de resultados consistentes ao longo dos estudos. A Figura 5 ilustra essa ideia.
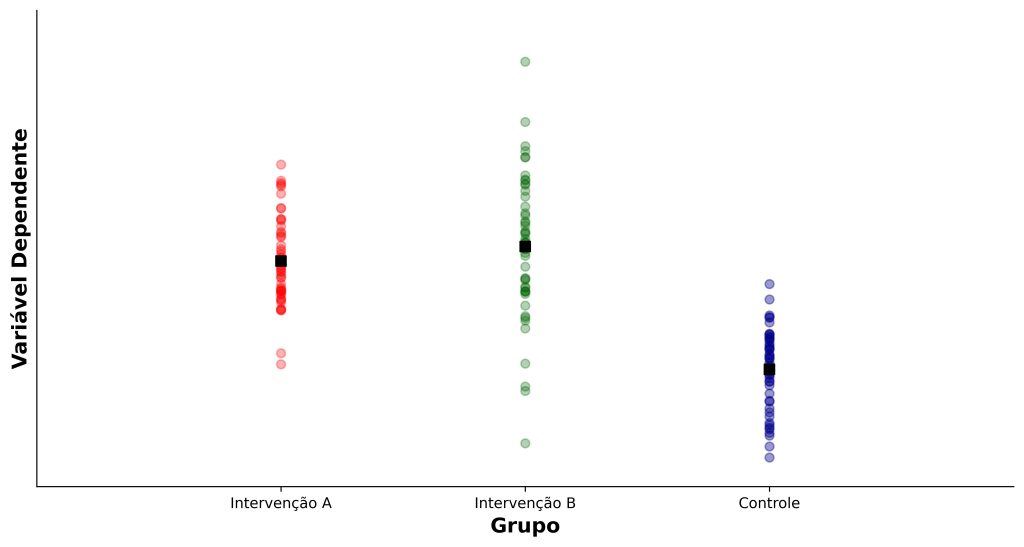
Por exemplo, suponha que queremos comparar um grupo intervenção com um grupo controle. Se nossa intervenção produzir efeitos mais homogêneos (Figura 5, Intervenção A), então teremos maior poder estatístico para detectar diferenças dessa condição em relação ao grupo controle. Em contrapartida, se nossa intervenção produzir efeitos mais heterogêneos (Figura 5, Intervenção B), então nosso poder estatístico para detectar diferenças em relação ao grupo controle será menor.
Tamanho da amostra
Por fim, o tamanho amostral é um fator crucial que afeta o poder estatístico. Essa relação está diretamente ligada ao conceito de erro-padrão. O erro-padrão indica quão precisamente um parâmetro é estimado na amostra. Assim, um erro-padrão baixo sugere que, em amostragens sucessivas, podemos esperar menor variabilidade nos valores das estimativas do parâmetro de interesse.
Por exemplo, suponha que estejamos interessados em estudar um certo grupo que acreditamos ter níveis de inteligência abaixo da média da população típica. Entre outros objetivos, queremos avaliar se a média dos escores de inteligência de nossa amostra difere significativamente da média da população típica (M = 100, DP = 15).
A Figura 6 apresenta duas distribuições. A distribuição do painel esquerdo se baseia em amostragens sucessivas e independentes com 10 participantes, enquanto a distribuição do painel direito se baseia em amostragens com 20 participantes. Em ambos os casos, as amostras são retiradas de uma população com M = 90 e DP = 15, isto é, cuja média é genuinamente distinta de 100, o valor esperado em uma população típica.
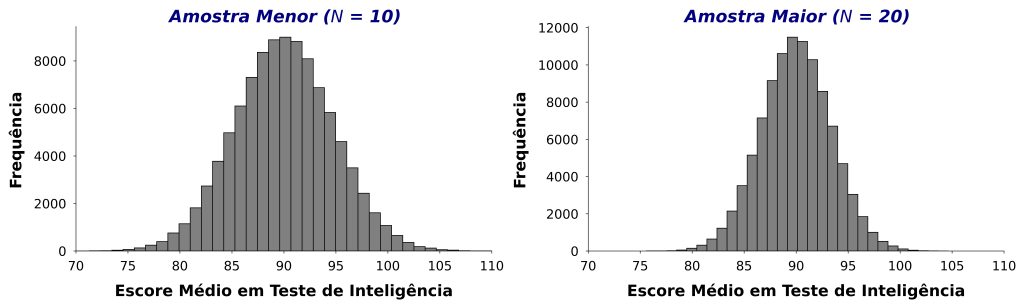
A Figura 6 sugere que, em uma amostra menor (painel esquerdo), as estimativas da média população variam mais em amostragens sucessivas. Por exemplo, eventualmente amostraremos algumas observações com escores de inteligência elevados e, consequentemente, falharemos em rejeitar a hipótese nula de que nossos dados vêm de uma população com M = 100 e DP = 15. Esse cenário, contudo, é mais improvável de acontecer quando o tamanho amostral aumenta (Figura 6, painel direito).
Qual é a importância do poder estatístico no planejamento de um projeto de pesquisa?
O poder para detectar um efeito depende da magnitude do efeito que queremos detectar
Anteriormente, vimos que tamanho de efeito e poder estatístico estão intimamente relacionados. Isso acontece porque, mantidos outros fatores constantes, quando o tamanho de efeito aumenta, o poder estatístico também aumenta.
Em seguida, discutiremos a importância do poder estatístico e como ele impacta o planejamento de pesquisa.
Exemplo de análise de poder a priori
Uma aplicação prática do conhecimento sobre poder estatístico é a análise de poder a priori. Por exemplo, considere um estudo sobre os níveis de curiosidade em cães e gatos. Com base em nossa expectativa de tamanho de efeito, podemos realizar uma análise de poder a priori utilizando o software G*Power. Essa análise é essencial para estimar o tamanho amostral necessário em um projeto de pesquisa, visando atingir um poder estatístico pré-estabelecido.
Por exemplo, suponha que queremos ser capazes de detectar, com um poder de 80%, a um nível de significância de 5%, um efeito do grupo sobre os níveis de curiosidade de d = 0,30. Além disso, definimos que os tamanhos grupais serão iguais e que nosso teste estatístico será bicaudal, isto é, sem expectativa da direção do efeito. A Figura 7 apresenta uma captura de tela do G*Power com as especificações dessa análise.
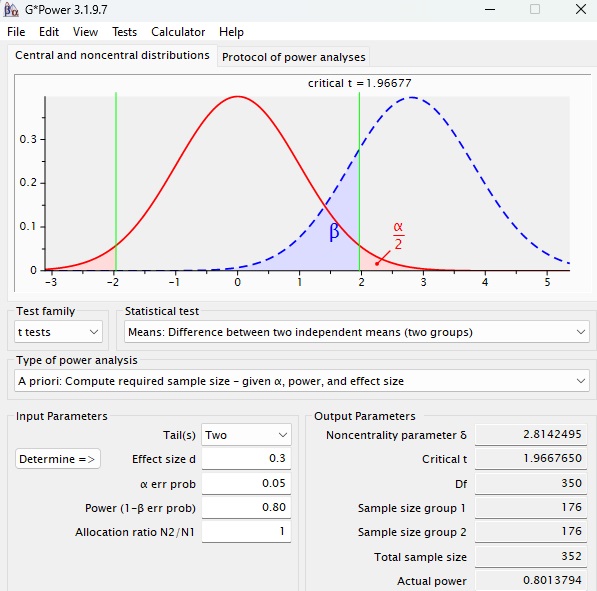
Com base na Figura 7, chegamos à seguinte conclusão: um delineamento que compara os níveis de curiosidade de cães e gatos necessita de pelo menos 176 sujeitos por grupo para ser capaz de detectar, com 80% de poder, um efeito de pelo menos d = 0,30, a um nível de significância de 5%.
Recomendamos o uso do G*Power, pois ele é um software gratuito, de fácil uso e que melhora a qualidade do planejamento de projetos de pesquisa.
Poder estatístico versus poder observado
Qual é a diferença entre poder estatístico e poder observado?
É fundamental diferenciar poder estatístico de poder observado. Uma prática comum na pesquisa científica é a coleta de dados, seguida da condução de testes estatísticos. Muitas vezes, os pesquisadores não encontram resultados estatisticamente significativos. Desse modo, por pressão de editores ou revisores, alguns pesquisadores calculam e relatam o poder observado do estudo. Contudo, estatísticos e metodólogos criticam essa prática (Gelman, 2018; Hoenig & Heisey, 2001; Lakens, 2014).
O poder estatístico (ou poder a priori) é a probabilidade de rejeitar uma hipótese nula falsa. Por outro lado, o poder observado (ou poder post hoc) é aquele obtido no teste estatístico conduzido em sua amostra, com base no tamanho de efeito estimado a partir dos dados. O poder observado é redundante no relato dos resultados, pois ele está intimamente relacionado ao valor de p. Assim, ele não fornece informações adicionais além daquelas já oferecidas pelo relato do teste estatístico.
Por que o poder observado não é informativo?
Vamos ilutrar o problema anteriormente descrito. Suponha que um pesquisador mensure os níveis de curiosidade de 33 cães e de 33 gatos (N = 66), com a expectativa de ser capaz de detectar um efeito de d = 0,50. Infelizmente, essa amostra tem apenas 51% de poder para detectar esse tamanho de efeito, valor considerado baixo (Figura 8).
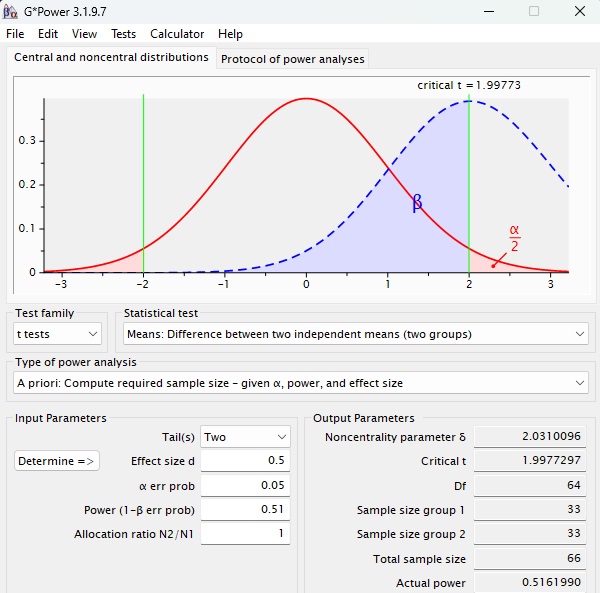
Esse pesquisador não detecta efeito significativo. Sendo assim, ele considera reportar o poder observado. Em seguida, mostraremos que isso é inútil.
Vamos simular 100 mil estudos hipotéticos, com N = 66, nível de significância de 0,05 e d = 0,50. Em cada simulação, computamos as estatísticas t e valores de p correspondentes, bem como o poder observado. Essas simulações, cujos resultados são apresentados na Figura 9, replicam os resultados de Lakens (2014).
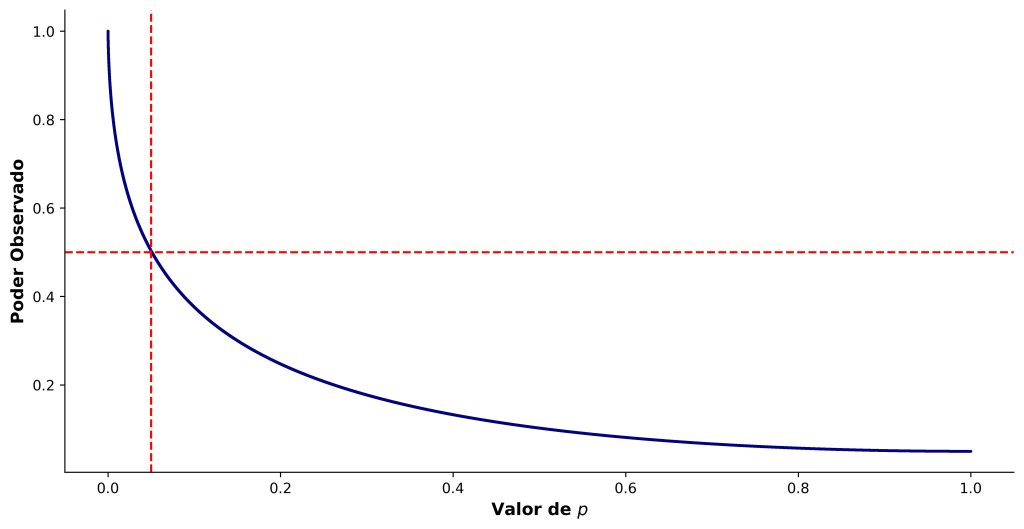
Como mostra a Figura 9, existe uma relação curvilínea negativa entre os valores de p e o poder observado. Embora os valores de poder observado variem de estudo para estudo, sabemos que, com base nos parâmetros da simulação, o poder estatístico (a priori) é de 51%.
Desse modo, concluímos que o poder estatístico (a priori) é fixo, enquanto o poder observado (post hoc) é variável e redundante em relação às demais informações apresentadas nos resultados. Este último é variável porque se baseia em estimativas, que são elas próprias sujeitas a flutuações, enquanto aquele primeiro se baseia em um parâmetro, considerado fixo em um dado delineamento de pesquisa.
Resumo
Em resumo, o poder estatístico é um conceito importante, especialmente durante a fase de planejamento de uma pesquisa, antes da coleta de dados. No G*Power, ele é definido pelo pesquisador na análise a priori. Por outro lado, o poder observado é calculado após a coleta de dados e estimado na análise post hoc no G*Power. Lakens (2014) considera o poder observado um conceito estatístico inútil e não recomenda seu uso, uma opinião que é compartilhada por Gelman (2018).
Para finalizar esta seção, apresentamos a reflexão de Hoenig e Heisey (2001, p. 23, livre-tradução): “Os cálculos de poder [a priori] nos informam quão bem seremos capazes de caracterizar a natureza no futuro, dado um determinado estado e desenho de estudo estatístico, mas eles [os cálculos post hoc] não podem usar as informações dos dados para nos informar sobre os prováveis estados da natureza”.
Conclusão
Neste post, explicamos o que é poder estatístico, quais fatores afetam o poder estatístico e qual é a importância desse conceito na fase de planejamento de um projeto de pesquisa. Além disso, diferenciamos o poder estatístico de um conceito de nome similar, mas enganoso e de pouca utilidade a pesquisadores (i.e., poder observado).
Gostou desse conteúdo? Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Gelman, A. (2018). Don’t calculate post-hoc power using observed estimate of effect size. Annals of Surgery, 269(1), e9–e10. https://doi.org/10.1097/SLA.0000000000002908
Hoenig, J. M., & Heisey, D. M. (2001). The abuse of power: The pervasive fallacy of power calculations for data analysis. The American Statistician, 55(1), 19–24.
Lakens, D. (2014, 19 de dezembro). Observed power, and what to do if your editor asks for post-hoc power analyses. The 20% Statistician [blog]. http://daniellakens.blogspot.com/2014/12/observed-power-and-what-to-do-if-your.html
Como citar este post
Lima, M. (2021, 9 de julho). Qual a importância do poder estatístico? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/qual-a-importancia-do-poder-estatistico/














