Você sabe qual é a diferença entre variância e desvio-padrão? Neste post, explicaremos como esses dois conceitos diferem. Além disso, também descreveremos o que os dois conceitos têm em comum.

O que são medidas de dispersão?
Quando falamos de variância e desvio-padrão, logo pensamos na variabilidade dos dados. Em estatística descritiva, a variabilidade (também chamada de espalhamento ou dispersão) consiste no quão diferentes são as observações de uma amostra.
Por exemplo, dois amigos, Carlos e Diego, caminharam em média 3 km por dia em uma determinada semana. No entanto, apesar de eles terem caminhado, em média, a mesma distância, Carlos foi mais regular em suas caminhadas diárias (Figura 1).

Por outro lado, Diego foi mais irregular durante a semana, alternando entre dias de caminhadas intensas e dias de nenhuma ou quase nenhuma caminhada (Figura 2).

Medidas de dispersão buscam descrever essas observações e discriminar conjuntos de dados com variabilidades distintas. Pesquisadores usam diferentes medidas de dispersão para analisar seus dados, incluindo, por exemplo, a amplitude, a amplitude interquartílica, a variância e o desvio-padrão. A seguir, discorreremos sobre as duas últimas, que são o foco deste post.

Variância e desvio-padrão: como calcular?
As fórmulas da variância e do desvio-padrão são muito parecidas. Primeiramente, calculamos a variância (s2) com base na seguinte fórmula:

onde x representa o escore da observação i em uma amostra, X-barra representa a média amostral, e N representa o tamanho amostral.
Por outro lado, calculamos o desvio-padrão (DP) com base na seguinte fórmula:

onde os símbolos têm o mesmo significado que na fórmula anterior.
Note que a principal diferença entre as duas fórmulas é que, no caso do desvio-padrão, tiramos a raiz quadrada do valor resultante da fração, enquanto isso não é feito no caso da variância. Matematicamente, o desvio-padrão é a raiz quadrada da variância:
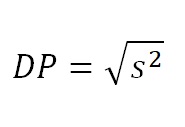
Ou, de forma similar, a variância é o quadrado do desvio-padrão:

Variância e desvio-padrão: exemplos de cálculo
Para facilitar o entendimento das fórmulas anteriores, vamos fazer uma decomposição delas em uma série de passos. Por exemplo, a variância pode ser calculada em cinco passos:
- 1º passo: calcular a média dos dados;
- 2º passo: calcular os desvios, definidos como as diferenças entre cada valor e a média;
- 3º passo: calcular os desvios quadráticos, definidos como os valores dos desvios (obtidos no 2º passo) elevados ao quadrado (os valores são elevados ao quadrado porque isso garante que desvios positivos e negativos não se anularão);
- 4º passo: somar os desvios quadráticos obtidos no 3º passo;
- 5º passo: dividir a soma obtida no 4º passo por N – 1 para obter o valor da variância.
Podemos calcular o desvio-padrão seguindo os mesmos cinco passos anteriores, com o acréscimo de mais um passo:
- 6º passo: calcular a raiz quadrada do valor obtido no 5º passo.
Aplicamos o algoritmo anteriormente apresentado aos dados de Carlos. A Figura 3 apresenta esses resultados, que indicam variância e desvios-padrões mais baixos, ou seja, s² = 0,50 km² e DP = 0,71 km.

Em seguida, fazemos o mesmo com os dados de Diego. A Figura 4 apresenta esses resultados, que indicam variância e desvios-padrões mais altos, isto é, s² = 6,50 km² e DP = 2,55 km.

Variância e desvio-padrão: qual deles reportar?
Tanto a variância quanto o desvio-padrão são medidas de dispersão que descrevem a variabilidade dos dados. No entanto, pesquisadores costumam preferir o desvio-padrão à variância no relato dos resultados de seus estudos.
Essa preferência se dá pelo fato de que a variância é expressa em unidades quadráticas. Isto é, na fórmula da variância, nós elevamos ao quadrado a diferença de cada escore em relação à média amostral. Sendo assim, nossas interpretações das variâncias dos escores de Carlos e Diego precisam ser feitas em quilômetros quadrados, o que é pouco alinhado com a nossa intuição.
Por outro lado, no desvio-padrão, calculamos a raiz quadrada dos desvios quadráticos médios, o que nos permite interpretar esse índice de variabilidade nas mesmas unidades da escala original – em quilômetros. Veja a diferença das duas interpretações:
- Interpretação usando a variância: embora Carlos e Diego tenham caminhado em média a mesma distância por dia ao longo da semana (Ms = 3 km), Diego teve caminhadas mais variáveis (s2 = 6,50 km²) que Carlos (s2 = 0,50 km²);
- Interpretação usando o desvio-padrão: embora Carlos e Diego tenham caminhado em média a mesma distância por dia ao longo da semana (Ms = 3 km), Diego teve caminhadas 3,61 vezes mais variáveis (DP = 2,55 km) ao longo dos dias que Carlos (DP = 0,71 km).
A diferença pode parecer sutil, mas é importante. Apenas no segundo caso é que avaliamos a razão entre os valores dos desvios-padrões, isto é, para fazermos afirmação do quão mais (ou menos) dispersas as observações de um dos amigos é em relação às observações do outro amigo.
Conclusão
Neste post, você aprendeu qual é a diferença entre variância e desvio-padrão. Por meio do desvio-padrão, podemos realizar análises cujas interpretações são mais alinhadas com nossas intuições, isto é, nas mesmas unidades que a nossa medida original.
No entanto, isso não quer dizer que a variância seja menos importante. Pelo contrário, a variância está presente em diferentes análises que compõem o arsenal de pesquisadores quantitativos, como as análises de variância (ANOVAs), além de aparecer também nas matrizes de variância–covariância da modelagem por equações estruturais.
Gostou desse conteúdo? Precisa aprender análise de dados? Então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Howell, D. C. (2013). Describing and exploring data. In D. C. Howell, Statistical methods for psychology (8th ed., pp. 15–62). Cengage Wadsworth Learning.
Como citar este post
Lima, M. (2022, 11 de fevereiro). Qual é a diferença entre variância e desvio-padrão? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/qual-e-a-diferenca-entre-variancia-e-desvio-padrao/













