O que é teste qui-quadrado de independência?

Neste post, explicaremos o que é o teste qui-quadrado de independência, como calculá-lo, interpretá-lo e reportá-lo.

Para que serve o teste qui-quadrado de independência?

O teste qui-quadrado de independência avalia se há diferenças estatísticas entre as frequências observadas e esperadas de casos que ocorrem em duas variáveis categóricas.

Em outras palavras, o teste compara as frequências que observamos no cruzamento de duas variáveis nominais ou ordinais com as frequências que seriam esperadas sob a hipótese nula de não associação entre as duas variáveis.

Por exemplo, suponha que avaliamos 100 adultos quanto aos hábitos de consumo de café (não consome, consome) e de qualidade de sono (não tem insônia, tem insônia). A Figura 1 apresenta uma tabela de contingências 2 × 2, isto é, uma representação que cruza a classificação nas duas variáveis para os 100 adultos de nossa amostra.

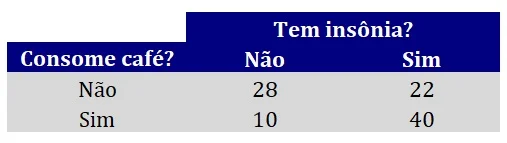
Nesse exemplo, desejamos explorar a relação entre duas variáveis categóricas nominais. Isto é, queremos responder à seguinte pergunta: existe associação entre consumo de café e insônia? Desse modo, veremos a seguir como calcular o teste qui-quadrado para dados oriundos desse delineamento hipotético.

Como calcular o teste qui-quadrado de independência?

A fórmula do teste qui-quadrado de independência é relativamente simples:

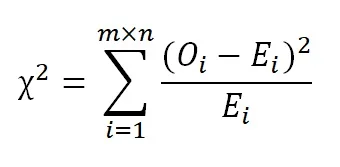
onde O_i corresponde à frequência observada na célula i, E_i corresponde à frequência esperada na célula i, m corresponde ao número de linhas, e n, ao número de colunas da tabela de contingências.

O χ² é uma estatística que reflete quão discrepantes são as nossas observações do que seria esperado sob a hipótese nula. Assim, você pode notar que se O = E para todas as células da tabela, então a estatística χ² será igual a zero. Por outro lado, quanto maior for a diferença entre O e E nas diferentes células, maior será a estatística χ².

A expressão “aquilo que seria esperado” se refere às expectativas de resultado sob a hipótese nula. Em nosso exemplo, a hipótese nula é a de que o consumo de café não está associado a sintomas de insônia. Em outras palavras, se isso for verdade, esperamos que os relatos de insônia entre quem consome e quem não consome café sejam aproximadamente iguais.

A Figura 1 apresentou as frequências observadas, O_i. Por outro lado, devemos calcular as frequências esperadas, E_i, com base nos totais marginais das frequências observadas. Apresentaremos esse cálculo a seguir.

Como calcular as frequências esperadas?

A Figura 2 reapresenta os dados da Figura 1, acrescida dos totais marginais, que correspondem às somas das linhas, das colunas e de todas as células da tabela de contingências.

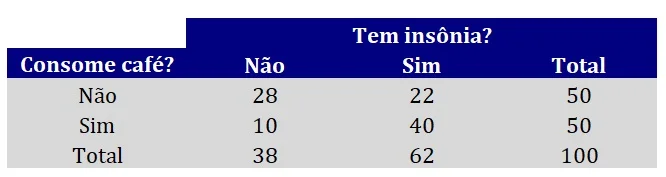
Além disso, também construíremos uma nova tabela, idêntica à anterior. Contudo, deixaremos as células inicialmente vazias. A Figura 3 apresenta essa nova tabela, que terá como finalidade representar as frequências esperadas sob a hipótese nula de não associação entre variáveis.

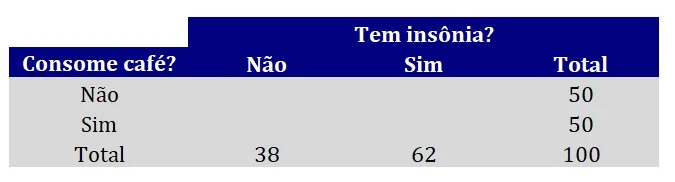
Em seguida, iremos preencher as células da tabela. A fórmula para preencher cada uma das células é dada por:

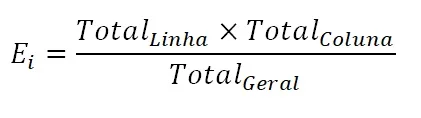
Por exemplo, vamos preencher a célula não consome café/não tem insônia. Desse modo, multiplicamos o total da linha não consome café (i.e., 50) e o total da coluna não tem insônia (i.e., 38) e dividimos seu resultado pelo total geral (i.e., 100). Assim, inserimos o valor resultante (50 × 38 / 100 = 19) como a frequência esperada nessa célula, sob a hipótese nula. A Figura 4 ilustra essa descrição.

O mesmo procedimento se repete para todas as células da tabela. Ao final do procedimento, teremos uma tabela similar àquela apresentada na Figura 5.

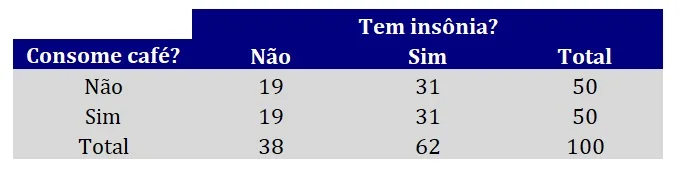
Pronto! Nossa tabela de contingências para frequências esperadas está preenchida. Contudo, lembre-se que após o termo “frequência esperada” está implícita a ideia de que é uma frequência esperada sob o pressuposto da hipótese nula de não associação entre variáveis.

Como calcular a estatística de qui-quadrado?

Agora que já temos as tabelas com as frequências observadas (Figura 1) e esperadas (Figura 5), podemos aplicar a fórmula do qui-quadrado. A Figura 6 decompõe a fórmula do qui-quadrado de independência em uma série de passos para, finalmente, computar a estatística do teste.

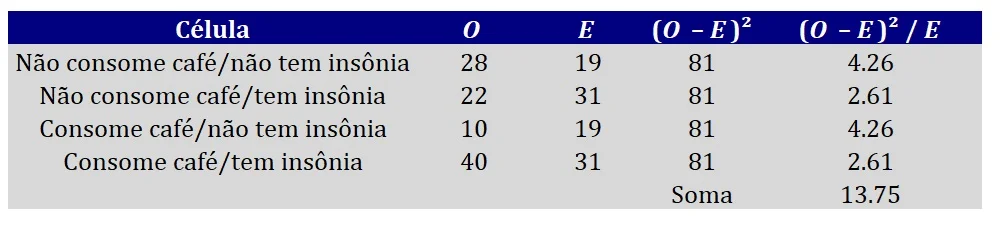
Na Figura 6, portanto, calculamos as diferenças entre valores observados e esperados para cada célula, elevamos esses desvios ao quadrado, e dividimos esses desvios quadráticos pelos valores esperados. Por fim, somamos os valores obtidos em todas as células. O valor da soma, isto é, 13,75, corresponde à estatística χ² observada em nossa amostra.

Quais são os resultados possíveis de um teste qui-quadrado de independência?

Quando calculamos a estatística χ², almejamos compará-la com um valor de referência, que é obtido de uma distribuição de χ² com graus de liberdade iguais ao de nossa amostra. No teste qui-quadrado de independência, o número de graus de liberdade (gl) é dado por gl = (m – 1)(n – 1). Em nosso exemplo, portanto, nosso teste tem 1 grau de liberdade.

A Figura 7 apresenta a distribuição de qui-quadrado com 1 grau de liberdade. Imagine que nosso objetivo é “fatiar” a distribuição no ponto exato em que teremos 95% da distribuição à esquerda, e 5% à direita do ponto de fatiamento.

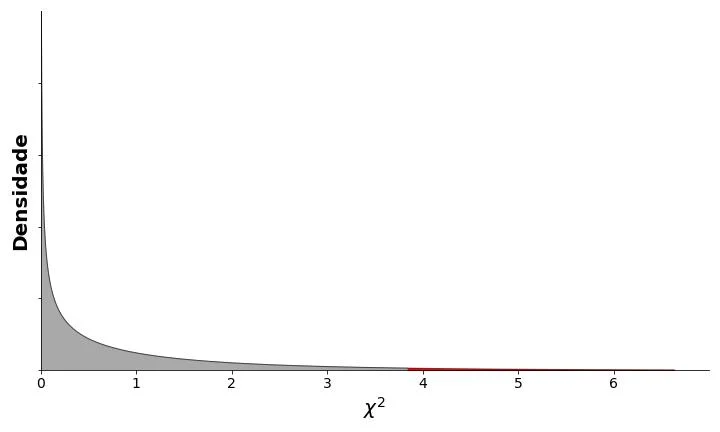
O valor de χ² correspondente a esse ponto de fatiamento é denominado χ² crítico que, na Figura 7, é de 3,84. Em outras palavras, ele corresponde ao ponto exato que divide as regiões cinza e vermelha da distribuição.

Ao comparar os valores de χ² observado e crítico da distribuição teórica da Figura 7, uma das seguintes situações poderá acontecer:

• χ²_observado < χ²_crítico: nesse caso, o valor que obtivemos cai na região cinza da Figura 7. Em outras palavras, falhamos em rejeitar a hipótese nula de que as frequências observadas e esperadas dos cruzamentos de consumo de café e relatos de insônia são iguais;
• χ²_observado > χ²_crítico: nesse caso, o valor que obtivemos cai na região de rejeição (a região vermelha da Figura 7). Em outras palavras, rejeitamos a hipótese nula de que as frequências observadas e esperadas dos cruzamentos de consumo de café e relatos de insônia são iguais.

Como interpretar o teste qui-quadrado de independência?

Recapitulando, devemos comparar a estatística χ² de nossa amostra com uma distribuição de χ², para avaliar se o valor obtido é igual ou mais extremo que o valor de χ² crítico para gl = 1.

Antigamente, isso era feito comparando-se o χ² obtido com uma tabela normatizada da distribuição de χ², que ainda aparece nos apêndices de alguns manuais de estatística. No entanto, com o advento de computadores modernos, isso não é mais necessário: softwares estatísticos nos fornecem facilmente o valor de p para o nosso teste.

Esse valor de p seria o equivalente a “fatiarmos” nossa distribuição no ponto exato de nosso χ²_observado e, posteriormente, calcular qual é a proporção da área à direita do fatiamento em relação à área total da distribuição inicial.

Em nosso exemplo, o χ² = 13,75, em uma distribuição com 1 grau de liberdade, está associado a um valor de p de 0,0002, que é inferior ao nosso nível de significância de 0,05. Por isso, rejeitamos a hipótese nula e interpretamos nossos resultados como indicativos de uma associação entre consumo de café e relatos de insônia.

Como calcular tamanhos de efeito do teste qui-quadrado de independência?

Três medidas de tamanho de efeito são tipicamente usadas em testes qui-quadrado de independência, a saber, o coeficiente phi (letra grega φ), o V de Cramér e a razão de chances (odds ratio).

Coeficiente phi

Podemos calcular o coeficiente φ diretamente a partir da estatística de qui-quadrado:

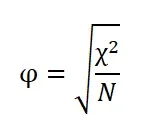
onde N é o total de observações da tabela de contingências. Em nosso exemplo, φ = √(13,75/100) = 0,37, o que podemos interpretar como uma associação moderada entre as variáveis. Note, contudo, que o coeficiente φ só deve ser calculado para tabelas de contingência 2 × 2.

V de Cramér

Nós também podemos calcular o V de Cramér a partir da estatística de qui-quadrado:

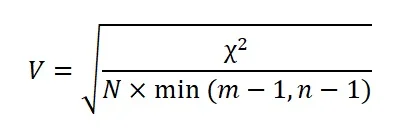
onde min(m – 1, n – 1) indica que devemos selecionar o menor entre os valores dos números de linhas e de colunas, subtraído de uma unidade. Se temos uma tabela de contingências 2 × 2, então min(m – 1, n – 1) = 1 e V = φ. No entanto, o V de Cramér é uma generalização do coeficiente φ para tabelas de contingência superiores a 2 × 2.

Razão de chances (odds ratio)

No presente exemplo, nós operacionalizaremos razão de chances como as chances relativas de quem consome café ter insônia, comparado a quem não consome café ter insônia. Para isso, rearranjamos os dados conforme a Figura 8, de modo a adequá-la à formula.

Em nosso exemplo, portanto, temos que a razão de chances (RC) = (40 × 28)/(10 × 22) = 5,09, indicando que quem consume café tem cinco vezes mais chances que quem não consome de ter insônia.

Como reportar os resultados do teste qui-quadrado de independência?

Os resultados de um teste qui-quadrado de independência devem fazer menção à estatística χ², aos graus de liberdade, ao valor de p e, finalmente, a uma medida de tamanho de efeito.

Desse modo, seguindo as normas de publicação da American Psychological Association (APA), 7ª edição, apresentamos uma sugestão de relato no parágrafo a seguir.

A Figura 1 apresenta a tabela de contingências cruzando as variáveis relacionadas ao consumo de café e sintomas de insônia. Com base nesses dados, um teste qui-quadrado de independência indicou que houve associação significativa e moderada entre consumo de café e insônia, χ²(1, N = 100) = 13,75, p < 0,001, φ = 0,37. Finalmente, a razão de chances indicou que aqueles que consome café têm 5,09 vezes mais chances de apresentar sintomas de insônia que aqueles que não consomem café.

Quais são os pressupostos do teste qui-quadrado de independência?

O teste qui-quadrado de independência possui alguns pressupostos estatísticos, isto é, algumas suposições devem ser satisfeitas para um adequado funcionamento do teste. Nesse teste, é importante que a frequência esperada mais baixa de cada célula seja maior ou igual a 5. No entanto, alguns autores sugerem um pressuposto menos rigoroso, a saber, pelo menos 80% das células devem ter frequências esperadas maiores ou iguais a 5.

Se você tiver uma tabela de contingências 2 × 2, é recomendado que a frequência esperada seja de pelo menos 10 por célula. Contudo, caso você viole tal pressuposto, é possível aplicar a correção de continuidade de Yates nos dados, ou usar o teste exato de Fisher. Ambas as alternativas estão disponíveis em pacotes estatísticos populares, como o SPSS e o JASP.

Conclusão

Neste post, você conheceu um pouco mais do teste qui-quadrado de independência. Além disso, você aprendeu como calculá-lo, interpretá-lo e reportá-lo. Se você quer aprender a realizar o teste qui-quadrado de independência em pacotes estatísticos, então veja nossos tutoriais no SPSS e no R.

Entretanto, lembre-se que o teste aqui apresentado não é o único que recebe a nomenclatura de “qui-quadrado”. Existe outro teste de nome parecido, denominado teste qui-quadrado de aderência, que considera a prevalência de casos nos níveis de uma única variável categórica.

Precisa aprender análise de dados? Então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).

Referências

Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5^th ed.). Sage.

Howell, D. C. (2013). Categorical data and chi-square. In D. C. Howell, Statistical methods for psychology (8^th ed., pp. 137–176). Wadsworth Cengage Learning.

Como citar este post

Lima, M. (2021, 4 de novembro). O que é teste qui-quadrado de independência? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/qui-quadrado-teste-de-independencia/