Reamostragem e o método bootstrap

Neste post, introduziremos o método bootstrap, uma técnica que cria novas amostras a partir da amostra original, por meio de amostragem com reposição, para estimar a precisão estatística. Primeiramente, descreveremos o que é reamostragem. Em seguida, apresentaremos a sequência de etapas envolvidas no método bootstrap. Além disso, apresentaremos um exemplo simples de implementação do método bootstrap. Por fim, elencaremos algumas das vantagens do uso dessa ferramenta no processo de inferência estatística.

O que é reamostragem?

Em estatística, amostrar consiste em selecionar elementos de uma população estatística. Por exemplo, suponha que o organizador de um evento enumere os ingressos para uma peça de teatro, de modo a realizar sorteios de brindes entre os presentes ao final da peça. Nesse exemplo, podemos pensar no número sorteado como uma amostra.

Vamos supor que o organizador sorteou o número 27. No entanto, existem outros brindes que serão sorteados. Se o organizador devolver esse número à urna, de modo que a mesma pessoa siga concorrendo aos demais brindes, então diremos que esse é um processo de amostragem com reposição. Em síntese, na amostragem com reposição, o mesmo elemento pode ser sorteado mais de uma vez.

A reamostragem consiste em criar novas amostras com base em uma amostra já observada. A Figura 1 ilustra esse conceito. Nela, temos uma amostra com os valores 1 a 10. Usando amostragem com reposição, criamos três novas amostras com base na amostra original.

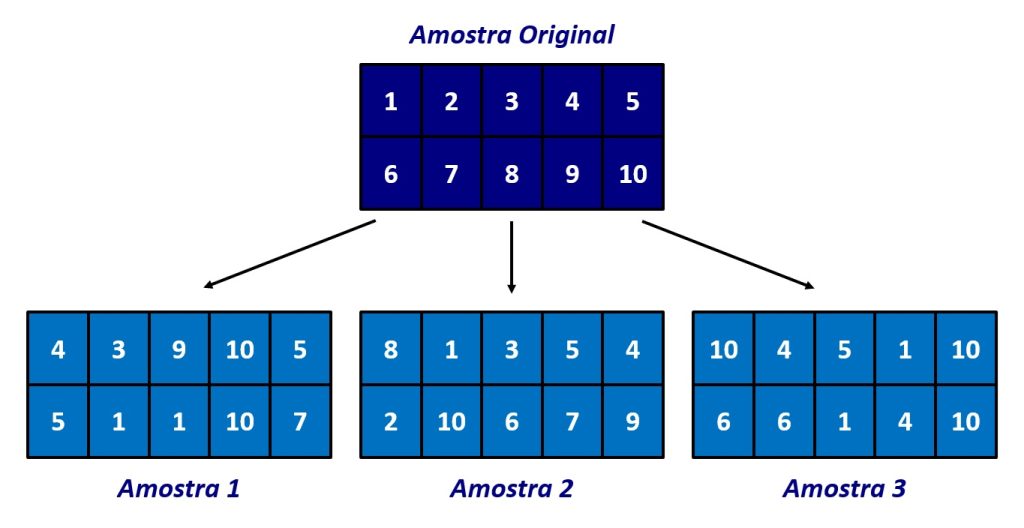
Note que, na Amostra 2, cada valor da amostra original aparece uma vez. No entanto, isso não ocorre nas Amostras 1 e 3. Por exemplo, os valores 2, 6 e 8 não aparecem na Amostra 1, enquanto os valores 1, 5 e 10 aparecem duas vezes cada. Na Amostra 3, o valor 10 ocorre três vezes. Como veremos mais adiante, essas novas amostras, no contexto do método bootstrap, são chamadas de amostras bootstrap.

O que é o método bootstrap?

Em pesquisas científicas, podemos usar nosso conhecimento sobre as propriedades de distribuições teóricas (e.g., normal, t) para construirmos intervalos de confiança ao redor de estatísticas (e.g., média). Isso nos permite fazer inferências sobre o valor do parâmetro populacional de nosso interesse.

No entanto, se nossos dados não aderem à distribuição normal, nossas inferências podem ser imprecisas. Além disso, podemos ter interesse em construir intervalos de confiança ao redor de outros valores, como a mediana ou o coeficiente de correlação de Spearman. Uma maneira alternativa de construir tais intervalos é por meio do método bootstrap.

O método bootstrap (ou bootstrapping) é um procedimento computacional que cria novas amostras a partir da amostra original para estimar a precisão estatística. Seu objetivo é, por meio de reamostragem, construir uma distribuição amostral empírica de uma estatística de interesse, permitindo assim que pesquisadores façam inferências estatísticas.

Por exemplo, para cada uma das amostras que construímos na seção anterior, poderíamos calcular estatísticas de nosso interesse, como médias e medianas. A Figura 2 reapresenta a Figura 1 com esses valores.

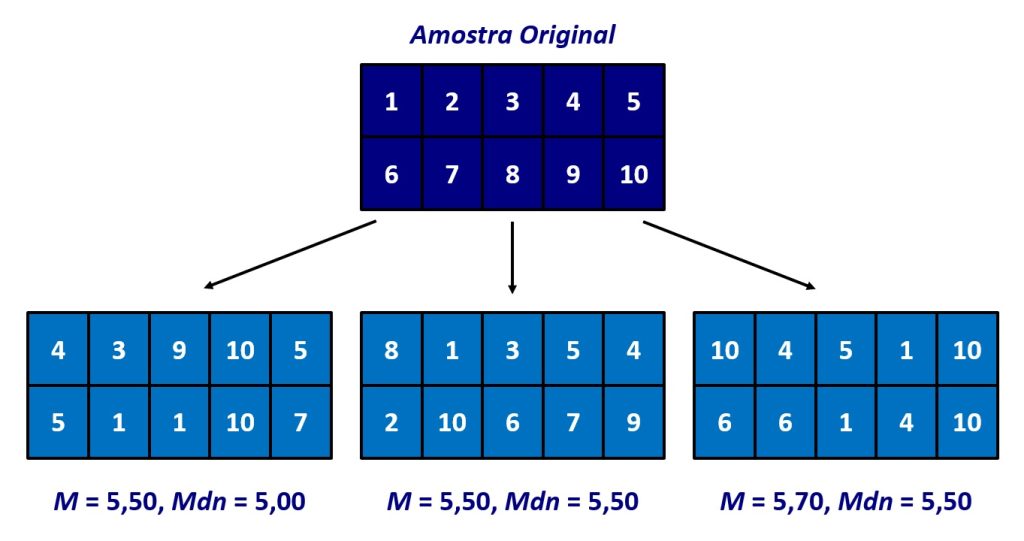
Com o poder de processamento de computadores modernos, podemos repetir esse procedimento centenas ou até mesmo milhares de vezes. Desse modo, ao invés de calcularmos o intervalo de confiança com base na estimativa do erro-padrão de nossa estatística, podemos usar a distribuição empírica obtida pelas múltiplas amostras bootstrap para estimar nosso intervalo de confiança.

Quais são as etapas do método bootstrap?

O método bootstrap provavelmente mais conhecido é o bootstrap não paramétrico, que assume que a distribuição da amostra reflete a distribuição da população. Podemos resumir esse método em três etapas (veja também a Figura 3):

1. Por meio de amostragem com reposição, criamos uma nova amostra, geralmente de tamanho similar ao de nosso banco de dados original;
2. Criamos replicações bootstrap de nossa estatística de interesse (e.g., média, mediana, correlação de Spearman, coeficiente de regressão);
3. Após k repetições dos passos 1 e 2, construímos uma distribuição amostral empírica da estatística de interesse e, a partir dela, computamos intervalos de confiança bootstrapped não paramétricos.

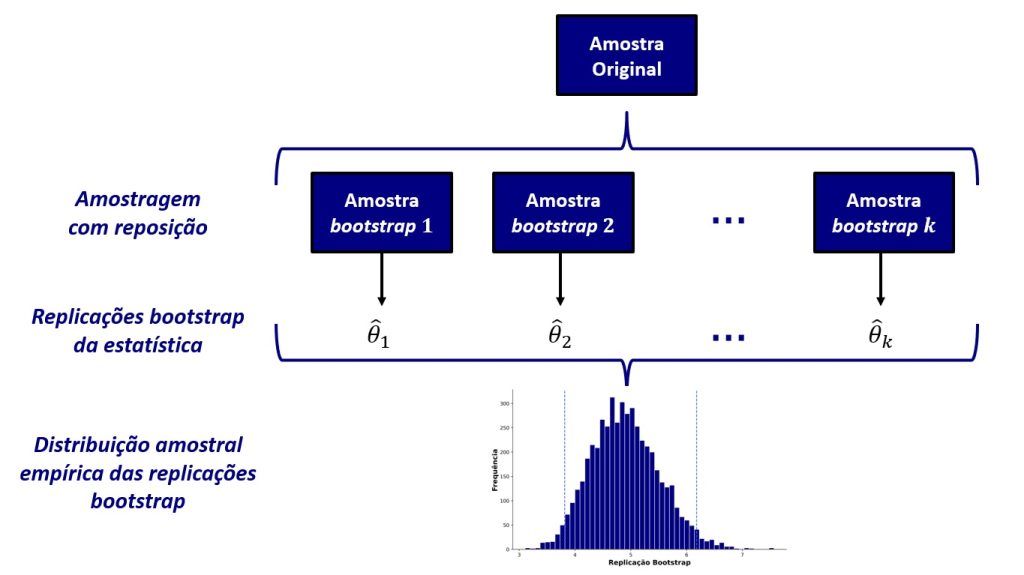
Nesse procedimento, o termo não paramétrico se refere ao fato de que não necessitamos especificar os parâmetros que descrevem o comportamento da distribuição populacional. Embora não seja nosso objetivo aqui discorrer sobre o bootstrap paramétrico, basta dizer que, nele, pesquisadores especificam os parâmetros da distribuição, de modo que as amostras bootstrap são obtidas a partir de distribuições teóricas, não da empírica.

Exemplo de implementação do método bootstrap

População e amostra

Vamos usar o método boostrap para estimar intervalos de confiança para a média e para a mediana. Em nosso exemplo, amostraremos 200 observações de uma distribuição lognormal com os parâmetros μ = 1 e σ = 1,2. Sendo assim, com base nesses parâmetros, a média populacional da distribuição lognormal é 5,58, e a mediana populacional, 2,72.

O painel esquerdo da Figura 4 apresenta os escores de nossa amostra. Nossa distribuição possui forte assimetria negativa. De fato, na distribuição lognormal, é o logaritmo natural da variável aleatória de interesse que possui distribuição normal (Figura 4, painel direito), mas não necessariamente a variável aleatória em si.

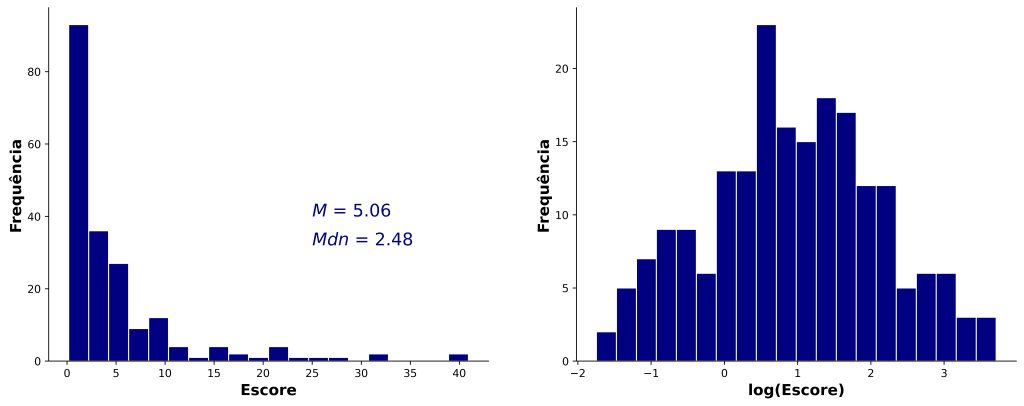
Note que, embora tenhamos fórmulas para calcular intervalos de confiança para a média e para a mediana, tais intervalos podem sofrer distorção pela não normalidade dos dados.

Gerando amostras bootstrap e calculando replicações bootstrap das estatísticas

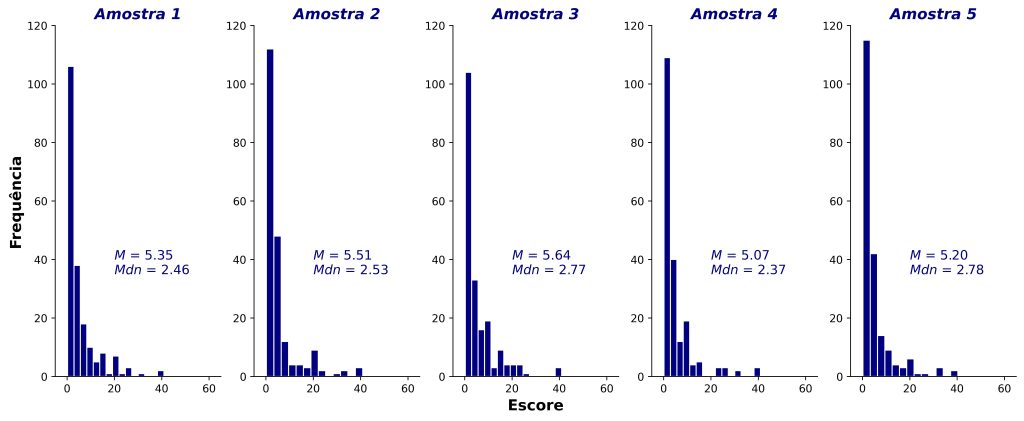
Em seguida, para demonstrar o método bootstrap, consideraremos os escores brutos (Figura 4, painel esquerdo). Para esse fim, vamos usar um procedimento de reamostragem, que amostrará 5.000 amostras com reposição, com 200 escores em cada amostra (i.e., o mesmo tamanho de nossa amostra). A Figura 5 ilustra as distribuições das cinco primeiras amostras bootstrap, com as médias e as medianas de cada uma dessas replicações.

As médias e as medianas de todas as amostras bootstrap serão armazenadas separadamente como replicações bootstrap de nossas estatísticas de interesse. Por fim, criaremos as distribuições amostrais empíricas da média e da mediana com base nas 5.000 amostras bootstrap (Figura 6).

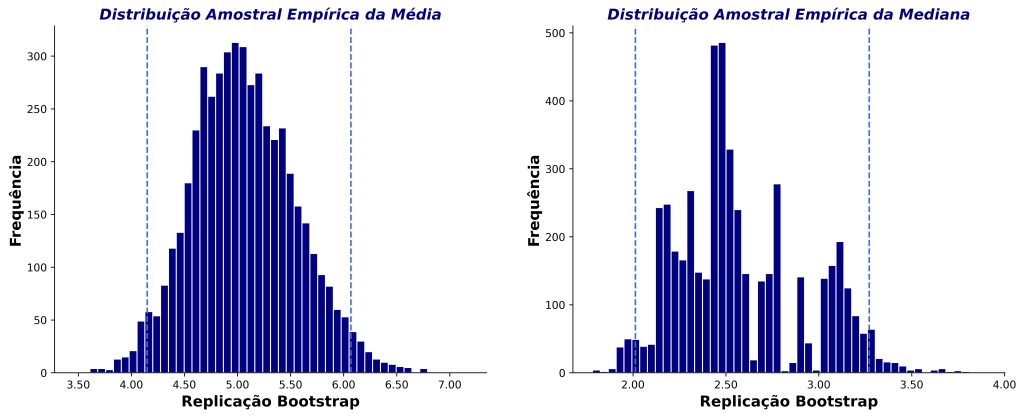
Note que a distribuição amostral empírica da média tem uma ligeira assimetria positiva. Isso é compreensível, pois as médias são influenciadas por valores extremos dos dados originais que foram incluídos em algumas das amostras bootstrap. Por outro lado, a distribuição amostral empírica da mediana tem menor variabilidade do que a da média, o que é consistente com o fato de que a mediana é menos afetada por valores extremos.

As linhas pontilhadas verticais da Figura 6 indicam as regiões de cada distribuição amostral empírica que separa os percentis 2,5 e 97,5 das replicações bootstrap. Desse modo, os valores das linhas pontilhadas representam nossos intervalos de confiança bootstrap percentílicos de 95%. No entanto, Field (2017) recomenda outra estimativa, denominada bias corrected and accelerated (BCa), que leva em consideração a assimetria da distribuição amostral empírica. Para fins didáticos, descreveremos apenas o intervalo de confiança percentílico.

Intervalos de confiança calculados pelo método tradicional e pelo método bootstrap

A Figura 7 apresenta os parâmetros populacionais da distribuição que gerou nossos dados, bem como as estatísticas amostrais e os intervalos de confiança estimados pelo método tradicional e pelo método bootstrap.

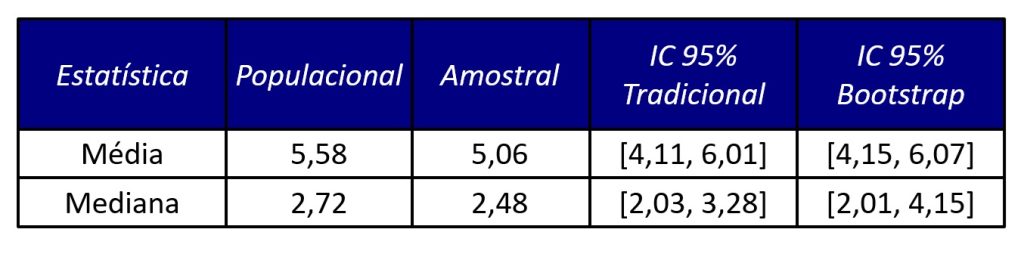
No presente exemplo, ambos os métodos capturaram os parâmetros de interesse. No entanto, em outras situações, o método bootstrap fornecerá estimativas mais confiáveis que o método tradicional.

Quais são as vantagens do método bootstrap?

Anteriormente, demos um exemplo bastante simples do uso do método bootstrap para construir intervalos de confiança ao redor da média e da mediana. Contudo, as vantagens do método se estendem para além disso.

Por exemplo, o método bootstrap permite estimar intervalos de confiança para qualquer estatística (e.g., mediana, coeficientes de regressão, correlações etc.), mesmo que não haja uma fórmula fechada para isso.

Além disso, essa técnica pode ser usada em uma série de análises bi e multivariadas, incluindo, por exemplo, análises de variância e seus testes post hoc. Essa vantagem é particularmente relevante porque o método bootstrap (não paramétrico) funciona bem até mesmo com distribuições desconhecidas, assimétricas ou complexas, desde que possamos assumir que os dados se parecem o suficiente com a população de modo a podermos tratá-los como uma “pseudopopulação”.

Embora tenhamos apresentado uma sequência de etapas da realização do bootstrap neste post, o objetivo foi fornecer uma compreensão conceitual do método. Contudo, ressaltamos que sua missão enquanto pesquisador(a) é a de interpretar as estatísticas, não de implementá-las etapa por etapa. Sendo assim, mais uma vantagem é que diversos pacotes estatísticos (e.g., SPSS, JASP) fornecem estimativas bootstrap de forma simples e acessível com um único clique.

Conclusão

Neste post, você aprendeu o que é o método bootstrap. Além disso, por meio de um exemplo, mostramos a lógica das etapas do método bootstrap. Por fim, nós também apresentamos algumas das vantagens dessa ferramenta no processo de inferência estatística.

Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a)

Referência

Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5^th ed.). Sage.

Haukoos, J. S., & Lewis, R. J. (2005). Advanced statistics: Bootstrapping confidence intervals for statistics with “difficult” distributions. Academic Emergency Medicine, 12(4), 360–365. https://doi.org/10.1197/j.aem.2004.11.018

Kline, R. B. (2016). Principles and practice of structural equation modeling (4^th ed.). The Guilford Press.

Como citar este post

Lima, M. (2024, 16 de dezembro). Reamostragem e o método bootstrap. Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/reamostragem-e-o-metodo-bootstrap/