A American Psychological Association recomenda que pesquisadores reportem medidas de tamanho de efeito e intervalos de confiança em seus resultados (Wilkinson & Task Force on Statistical Inference, 1999). Uma dessas medidas, que será o tema deste post, é o delta de Glass.
Neste post, descreveremos o que é o delta de Glass. Além disso, discutiremos em quais situações ele é preferível a outras medidas de tamanho de efeito. Por fim, mostraremos, por meio de um exemplo, como calculá-lo e interpretá-lo.

O que são tamanhos de efeito da família d?
Tamanhos de efeito da família d expressam a diferença entre duas médias grupais em unidades padronizadas. Por exemplo, podemos comparar grupos medicamento versus placebo, solteiros versus casados, jovens adultos versus idosos, em função de alguma variável dependente de interesse.
Suponha que designamos aleatoriamente os participantes a uma de duas condições, a saber, experimental e controle. Nesse sentido, tamanhos de efeito da família d estimam a distância do centro das duas distribuições (i.e., as médias) em uma escala que considera o grau de espalhamento dos escores nas duas distribuições (i.e., os desvios-padrões), tal como ilustra a Figura 1.

Na Figura 1, as variâncias das distribuições são iguais, casos em que duas medidas da família d – o d de Cohen e o g de Hedges – são adequadas.
Contudo, em algumas pesquisas, a variável independente pode influenciar não apenas as médias (que é o que queremos comparar quando usamos um teste t), mas também as variâncias ou desvios-padrões dos grupos.
Por exemplo, se uma dada manipulação afeta apenas uma parte dos participantes designados à condição experimental, é possível que a variabilidade nos escores desse grupo aumente. Nesse caso, o pressuposto de homogeneidade de variâncias não se mantém. A Figura 2 ilustra o cenário em que duas distribuições diferem não apenas em termos de suas médias, mas também de seus desvios-padrões.

As fórmulas do d de Cohen e do g de Hedges consideram os desvios-padrões dos dois grupos. Desse modo, se os dois desvios-padrões forem heterogêneos, então essas medidas podem fornecer uma visão inacurada dos resultados.
O que é o delta de Glass?
O delta de Glass (ou ∆ de Glass, do inglês Glass’s delta) é uma medida de tamanho de efeito que padroniza a diferença entre médias com base no desvio-padrão do grupo controle:

Podemos interpretar o delta de Glass como a diferença entre grupo experimental e controle em unidades do desvio-padrão do grupo controle. Com base na Figura 2, consideraríamos apenas a distribuição azul no cálculo do delta de Glass.
Desse modo, o delta de Glass é útil quando as variâncias grupais diferem substancialmente. Além disso, ele também é útil quando temos múltiplas condições experimentais, e queremos contrastar cada condição experimental com uma mesma condição controle. Nesse caso, todas as comparações em pares representarão a diferença da condição experimental específica para a condição controle, em unidades de desvio-padrão dessa condição controle.
Como calcular e como interpretar o delta de Glass?
Participantes passaram por um procedimento de indução de humor, isto é, eles ouviram uma música instrumental para induzir humor negativo (Negativo), uma música para induzir humor positivo (Positivo) ou um ruído branco como condição controle (Controle).
Dez participantes foram designados a cada condição. Além disso, os níveis de humor pós-tarefa foram mensurados. Os resultados estão na Figura 3, onde escores baixos indicam humor negativo, enquanto escores altos indicam humor positivo.
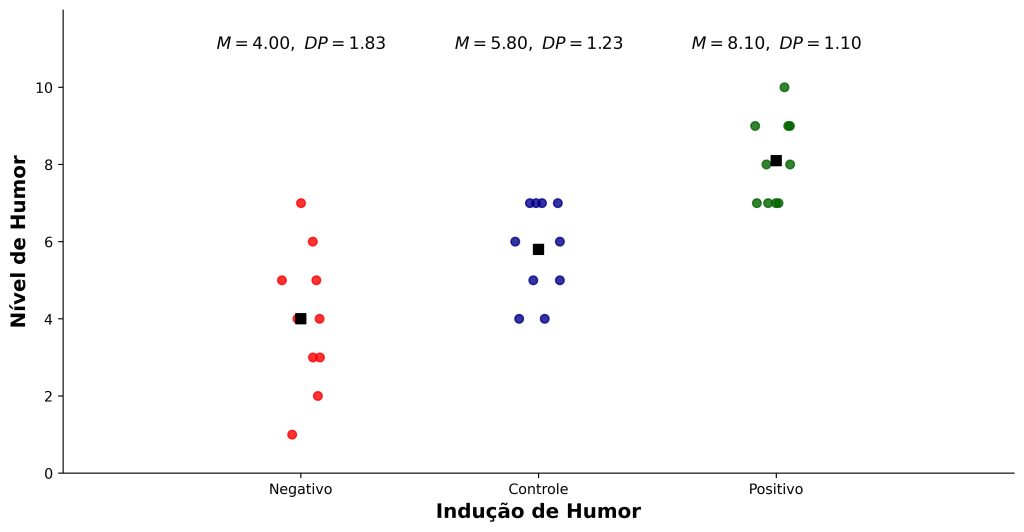
Note que, comparado à condição controle, a indução de humor negativo resultou em menores níveis de humor, mas com maior desvio-padrão, sugerindo efeitos heterogêneos entre participantes. Por outro lado, na indução de humor positivo, os escores de humor aumentaram de forma mais homogênea.
A Figura 4 apresenta tamanhos de efeito para os contrastes entre os grupos de indução de humor e o grupo controle. Primeiramente, na comparação entre os grupos positivo e controle, Δ = (8,10 – 5,80) / 1,23 = 1,87, indicando que a indução de humor positivo aumentou os níveis de humor em 1,87 desvio-padrão do grupo controle.

Em contrapartida, na comparação entre os grupos negativo e controle, Δ = (4,00 – 5,80) / 1,23 = –1,46, mostrando que a indução de humor negativo reduziu os níveis de humor em 1,46 desvio-padrão do grupo controle.
Embora os cálculos do d de Cohen não sejam o foco aqui, vale notar que, no contraste positivo vs. controle, o d de Cohen foi maior que o delta de Glass, pois o desvio-padrão do grupo positivo (considerado no cálculo do d) é menor que o do grupo controle. Por outro lado, no contraste negativo vs. controle, o oposto aconteceu.
Conclusão
Neste post, você aprendeu o que é o delta de Glass, uma medida de tamanho de efeito que quantifica a diferença padronizada entre duas médias. Recomendamos também que você conheça o d de Cohen e o g de Hedges.
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Lakens, D. (2013). Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Frontiers in Psychology, 4, Article 863. https://doi.org/10.3389/fpsyg.2013.00863
Wilkinson, L., & Task Force on Statistical Inference. (1999). Statistical methods in psychology journals: Guidelines and explanations. American Psychologist, 54(8), 594–604. https://doi.org/10.1037/0003-066X.54.8.594
Como citar este post
Lima, M. (2024, 2 de dezembro). O que é o delta de Glass (Glass’s delta)? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/tamanho-de-efeito-delta-glass-glass-delta/













