Neste post, descreveremos o g de Hedges, uma medida de tamanho efeito usada para avaliar a magnitude da diferença entre duas médias. Mostraremos que o g de Hedges visa superar uma limitação que o d de Cohen possui. Por meio de exemplos, mostraremos como calculá-lo e como interpretá-lo. Por fim, faremos uma importante ressalva sobre a ambiguidade da nomenclatura usada na literatura científica.
O que é o g de Hedges?
O g de Hedges (Hedges’s g) consiste em uma medida de tamanho de efeito usada para avaliar a magnitude da diferença entre duas médias. O g faz parte da família d de tamanhos de efeito, que também inclui o d de Cohen e o delta de Glass.
Por exemplo, suponha que designamos aleatoriamente os participantes aos grupos experimental e controle. Nesse experimento, queremos avaliar diferenças desses grupos em função de alguma variável dependente de interesse. Nesse cenário, além de conduzirmos um teste t para amostras independentes, também podemos reportar o g de Hedges como medida de tamanho de efeito.

O que é o d de Cohen?
O d de Cohen é uma medida de tamanho de efeito conceitualmente semelhante ao g de Hedges. Uma vez que o g de Hedges consiste em uma correção do d de Cohen, é relevante revisarmos brevemente o d. Sua fórmula é:
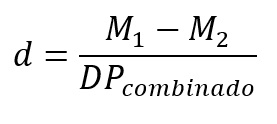
E calculamos o desvio-padrão combinado, no denominador, da seguinte maneira:
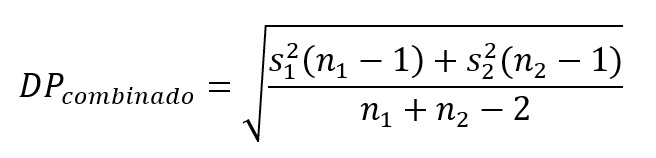
onde s12 e s22 representam as variâncias dos grupos, enquanto n1 e n2 representam os tamanhos dos grupos. Embora pareça complexa, a fórmula do desvio-padrão combinado consiste em uma média aritmética ponderada das estimativas de variabilidade dos dois grupos.
Qual é a diferença entre o g de Hedges e o d de Cohen?
O d de Cohen superestima o tamanho de efeito populacional, ou seja, ele é um estimador enviesado da diferença padronizada entre médias. Desse modo, metodólogos desenvolveram um fator de correção que, quando multiplicado pelo d, produz o g de Hedges, um estimador não enviesado da diferença entre médias.
Antes de apresentarmos o cálculo do g de Hedges, mostraremos, por meio de uma simulação, o que queremos dizer com estimadores enviesados e não enviesados. Considere que temos duas populações que, em uma variável de nosso interesse, possuem médias iguais a 0 e a 0,5, mas com um desvio-padrão comum igual a 1. Nesse exemplo, portanto, as médias populacionais diferem em meia unidade de desvio-padrão, pois (0,5 – 0) / 1 = 0,5.
Em seguida, selecionamos amostras dessas duas populações e calculamos o d de Cohen e o g de Hedges. Fazemos isso para diferentes tamanhos grupais, variando de 5 até 100, em incrementos de 5 participantes por grupo. Isso totaliza 20 cenários distintos. Em cada um deles, repetimos o processo de amostragem 100 mil vezes e, por fim, calculamos os ds e gs médios de cada cenário. A Figura 1 apresenta os resultados das simulações.
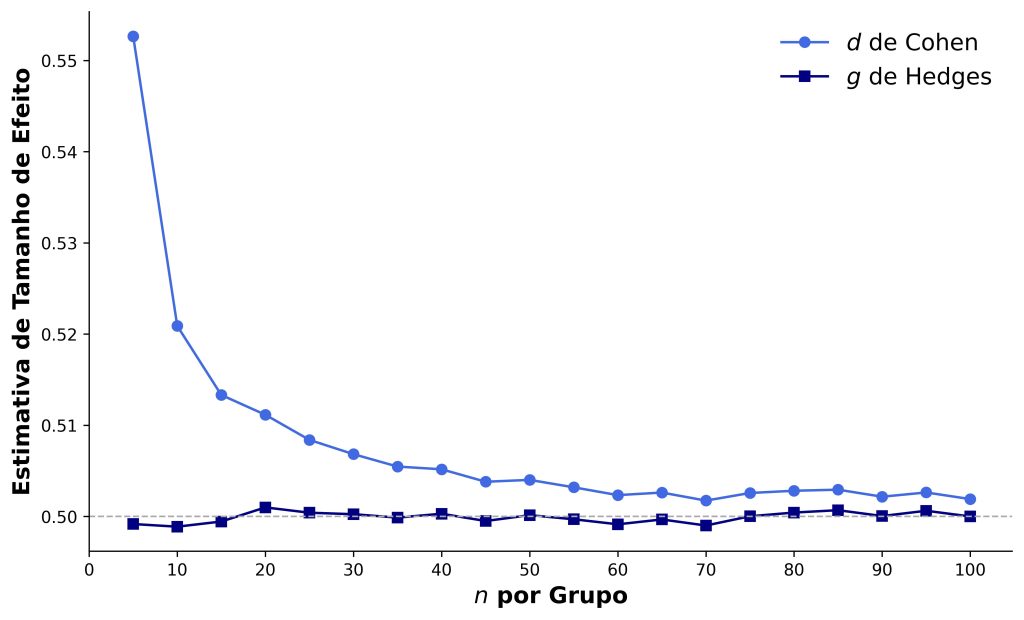
Note que, em todos os cenários, o valor do d de Cohen superestima o tamanho de efeito verdadeiro. Além disso, esse viés é maior em tamanhos amostrais menores, com viés maior que 10% quando cada grupo tem 5 participantes.
Em contrapartida, o g tende ao valor verdadeiro. Logo, o g de Hedges, mas não o d de Cohen, é um estimador não enviesado do tamanho de efeito populacional.
Como calcular e como interpretar o g de Hedges?
Anteriormente, dissemos que o g consiste no d multiplicado por um fator de correção (J). Embora exista um cálculo exato para o J, ele envolve a função gama e o cálculo de fatorial, o que complicaria desnecessariamente a nossa explicação (para a fórmula, veja Goulet-Pelletier & Cousineau, 2018). No entanto, existe uma boa aproximação para o J, cujo cálculo é bem mais simples:
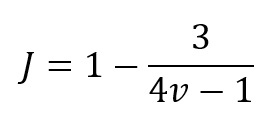
onde v = n1 + n2 – 2, em delineamentos entressujeitos; e v = 2(N – 1), em delineamentos de medidas repetidas. O ponto importante é que o J sempre será menor que 1. Quanto maior for o tamanho amostral, mais J se aproximará de 1, implicando um fator de correção pequeno.
Por outro lado, em tamanhos amostrais menores, o J será bem menor (e.g., J ≅ 0,57, quando os tamanhos grupais são iguais a 2), o que leva a uma correção maior – justamente quando ela é mais necessária.
Calculamos o g da seguinte maneira:
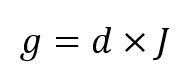
Foi essa a fórmula que usamos na simulação da seção anterior.
Os valores do g de Hedges variam de –∞ a +∞, mas, de forma mais realista, costumam variar em torno de –3 a +3. Valores iguais a 0 indicam que não há diferença entre as médias grupais. Seguindo a sugestão de Cohen (1988), gs iguais a 0,20, 0,50 e 0,80 são considerados pequenos, médios e grandes, respectivamente. No entanto, recomendamos fortemente que você inteprete o g à luz da literatura de sua própria área de pesquisa.
Exemplos de cálculo do g de Hedges
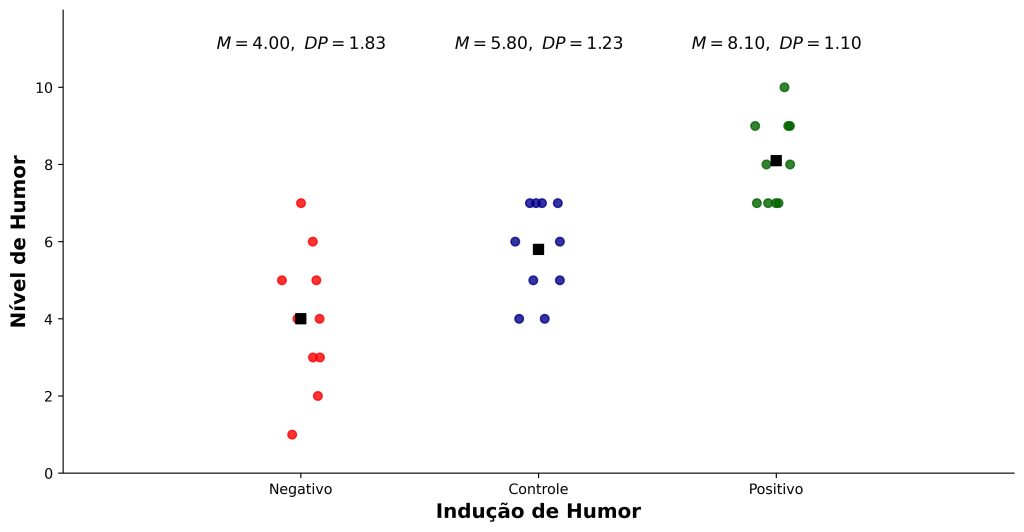
Eis um cenário hipotético. Pesquisadores tentaram induzir diferentes estados de humor nos participantes. A variável dependente consistiu no nível de humor, onde escores baixos indicam humor negativo, enquanto escores altos indicam humor positivo.
Eles pretendiam checar se, comparado ao grupo controle, a indução de humor foi bem sucedida nos grupos positivo e negativo. A Figura 2 apresenta os resultados.
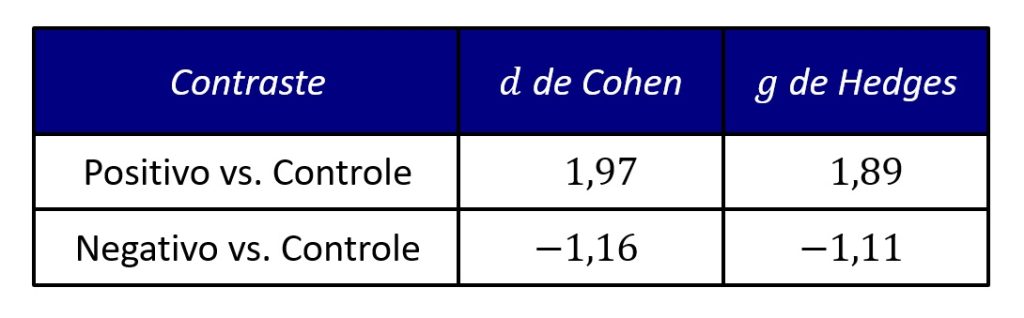
A Figura 3 compara os grupos positivo e negativo com o grupo controle.
Como há 10 participantes por grupo, o J é aproximado por:
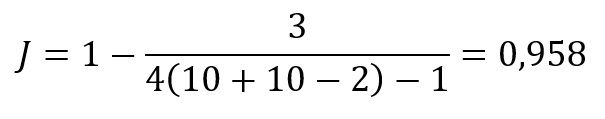
Portanto, o g terá aproximadamente 95,8% do valor de d:
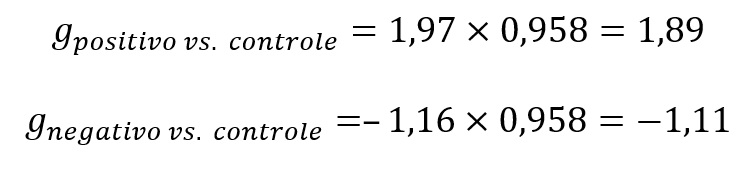
Concluímos que a indução de humor produziu os efeitos esperados: em comparação ao grupo controle, os níveis de humor aumentaram no grupo positivo (g = 1,89), mas diminuíram, no grupo negativo (g = –1,11). Como nossa amostra é pequena, o g é mais confiável que o d para estimar os efeitos do procedimento de indução de humor.
Um alerta importante sobre a nomenclatura usada na literatura
Infelizmente, alguns pesquisadores usam o termo g de Hedges para se referir ao d de Cohen, isto é, o estimador enviesado de tamanho de efeito. Em contrapartida, outros chamam o g de Hedges de dunb ou de dunbiased, onde unbiased é o termo em inglês que significa não enviesado.
O d e o g têm interpretações idênticas. O que difere entre eles, como vimos, é que só o g é um estimador não enviesado do efeito populacional. Se um pesquisador calcula o d de Cohen, mas o chama de g de Hedges, você pode erroneamente acreditar que ele usou um estimador livre de viés.
Isso é um problema se você usar esse valor para calcular o seu tamanho amostral no G*Power, pois, se o efeito obtido superestimou o tamanho do efeito verdadeiro, um cálculo de tamanho amostral baseado nele poderá sugerir uma amostra inferior àquela realmente necessária para o estudo.
Na prática, recomendamos que você sempre deixe explícito quais fórmulas está usando em seus artigos, quer apresentando as fórmulas no próprio texto ou remetendo o leitor ao artigo original no qual você se baseou (e.g., “para a fórmula do d de Cohen, veja a Equação 1 de Lakens (2013)”).
Além disso, quando estiver em dúvida sobre qual valor foi apresentado em estudos que você está lendo, tente reproduzir os cálculos usando as fórmulas que você conhece. Todavia, vale ressaltar que o g de Hedges, embora seja um estimador não enviesado, é pouco usado na literatura primária. Sua maior presença ocorre em revisões metanalíticas da literatura científica.
Conclusão
Neste post, você aprendeu o que é o g de Hedges, uma medida de tamanho de efeito que quantifica a diferença padronizada entre duas médias. Embora aqui tenhamos apresentado as fórmulas do d de Cohen e do g de Hedges, você provavelmente nunca precisará calculá-las manualmente. Diversos pacotes estatísticos (e.g., JASP, R) calculam, de forma rápida e precisa, essas medidas para você.
Gostou desse conteúdo? Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referência
Cumming, G. (2012). Understanding the new statistics: Effect sizes, confidence intervals, and meta-analysis. Routledge.
Goulet-Pelletier, J.-C., & Cousineau, D. (2018). A review of effect sizes and their confidence intervals, Part I: The Cohen’s d family. The Quantitative Methods for Psychology, 14(4), 242–265. https://doi.org/10.20982/tqmp.14.4.p
Lakens, D. (2013). Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Frontiers in Psychology, 4, Article 863. https://doi.org/10.3389/fpsyg.2013.00863/full
Como citar este post
Lima, M. (2024, 2 de dezembro). Tamanho de efeito: g de Hedges (Hedges’s g). Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/tamanho-de-efeito-g-de-hedges-hedges-g/














Respostas de 4
Caro Bruno,
Sempre agradeço a qualidade do seu trabalho e o fato de que sempre que preciso recuperar alguma fórmula ou buscar alguma boa referência encontro as respostas em seus posts e vídeos.
No caso deste post, preciso deixar uma observação complementar: o g de Hedge não varia de -1 a 1. Os tamanho de efeito podem ser maiores que 1.
Deixo números de exemplo real aqui: M1 = 2,9327; S1 = 0,57139; N1 = 48 e M2 = 2,2269; S2=0,47318; N2=20 –> g = 1,295 (pela própria fórmula que você apresenta).
Abraços!
Olá Isabel,
Ficamos felizes em saber que nossos posts e vídeos tem sido úteis.
Agradecemos o seu retorno em relação a este post.
Embora revisamos e monitoramos cada post, vamos nos atentar ainda mais aos detalhes.
Equipe Psicometria Online Academy
Não seria legal ter um link com o como citar essa página (modelo)? Tem até alguns repositórios que salvam e poderia ser citada assim. Está cada vez mais comum essa prática entre os novos pesquisadores.
Oi, Murilo. Vamos incluir as informações sobre como citar os posts do blog a partir deste mês. Muito obrigado pela sugestão!
Equipe Psicometria Online Academy