Neste post, falaremos sobre o teste de Levene. Primeiramente, abordaremos o conceito de homogeneidade das variâncias. Em seguida, introduziremos o teste de Levene propriamente dito, explicitando suas hipóteses nula e alternativa. Nós então apresentaremos os resultados de dois testes de Levene, indicando como interpretá-los. Por fim, mostraremos um código simples que permite executar o teste de Levene no R.
O que é homogeneidade das variâncias?
Antes de mais nada, é importante compreendermos o conceito de homogeneidade das variâncias. A homogeneidade das variâncias é um pressuposto estatístico subjacente a muitos testes estatísticos paramétricos, como o teste t de Student e a análise de variância (ANOVA) de uma via.
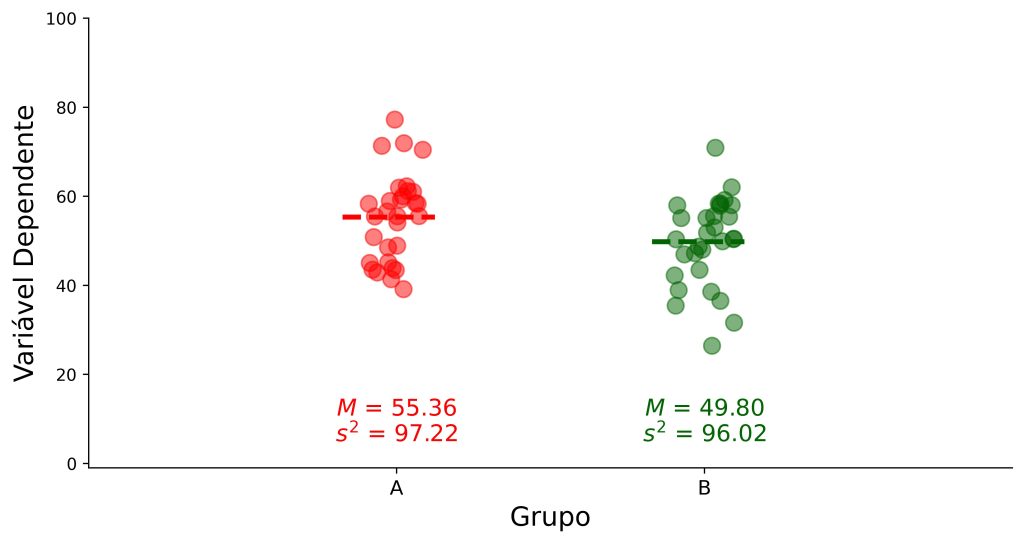
Em síntese, quando assumimos homogeneidade das variâncias em nossos dados, pressupomos que as variâncias das diferentes amostras ou grupos de dados devem ser semelhantes entre si. A Figura 1 apresenta um gráfico comparando os Grupos A e B numa variável dependente qualquer. Podemos ver que as variâncias dos escores da variável dependente nos dois grupos são relativamente homogêneas.
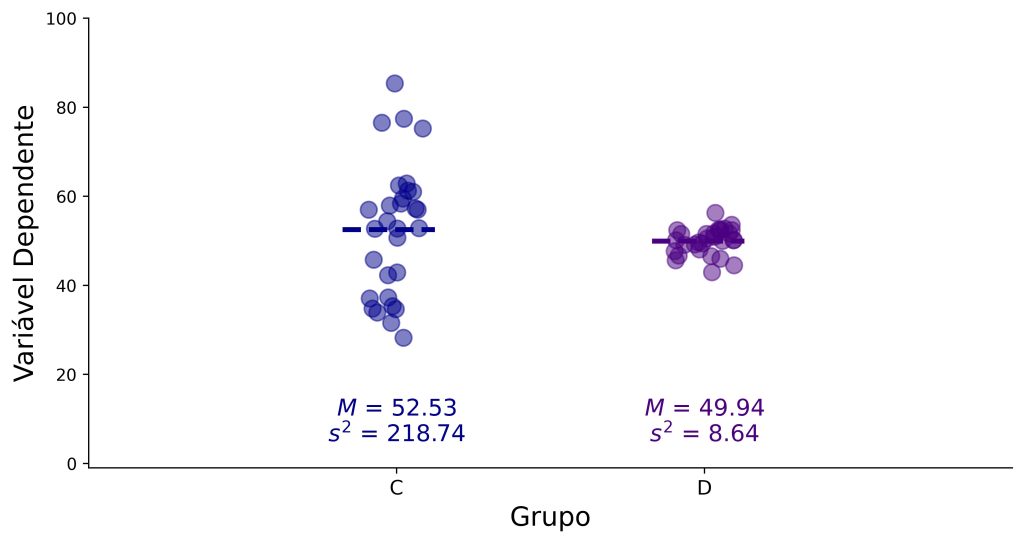
Por outro lado, a Figura 2 contrasta os Grupos C e D numa variável dependente qualquer. Ao contrário do que acontece no exemplo anterior, observa-se que as variâncias dos escores da variável dependente nos dois grupos são relativamente heterogêneas: a variabilidade no Grupo C é muito superior à variabilidade no Grupo D.
Se o pressuposto de homogeneidade das variâncias não for satisfeito em nossa amostra, então os resultados dos testes estatísticos que assumem homogeneidade das variâncias podem ser imprecisos. Desse modo, o teste de Levene visa nos auxiliar a decidir se temos evidência forte o suficiente para rejeitarmos o pressuposto de homogeneidade das variâncias.

O que é o teste de Levene?
A fim de examinar o pressuposto de homogeneidade das variâncias, é necessário realizar o teste de Levene. Esse teste compara a variância das amostras com a variância geral e é usado como um passo inicial antes de realizar testes paramétricos, como o teste t de Student e a ANOVA de uma via.
O teste de Levene possui as seguintes hipóteses nula (H0) e alternativa (H1):
- H0: os grupos têm variâncias iguais (dados homocedásticos);
- H1: os grupos têm variâncias diferentes (dados heterocedásticos).
O teste de Levene gera uma estatística F e um valor de p a ela associado. Para fins de interpretação do valor de p, assumiremos na sequência do post que adotamos o nível de significância convencional de 0,05. Sendo assim, temos duas decisões possíveis:
- Se p < 0,05, então as variâncias diferem significativamente entre os grupos. Em outras palavras, rejeitamos o pressuposto de homogeneidade das variâncias;
- Se p > 0,05, então as variâncias não diferem estatisticamente entre os grupos. Ou seja, não rejeitamos o pressuposto de homogeneidade das variâncias.
Note que este padrão de interpretação difere do que estamos acostumados em estatística frequentista. Geralmente, quando queremos corroborar a hipótese de que um tratamento gerou diferenças entre grupos, desejamos obter um valor de p menor que 0,05. Em contrapartida, para não abandonarmos o pressuposto de homogeneidade das variâncias, almejamos obter um valor de p maior que 0,05.
Exemplos de testes de Levene
Para fins de interpretação, vamos apresentar os resultados dos testes de Levene examinando os pressupostos de homogeneidade das variâncias para os exemplos das Figuras 1 e 2.
Relembrando, na Figura 1, as variâncias foram relativamente homogêneas. O teste de Levene foi consistente com esse padrão, F(1, 58) = 0,04, p = 0,84. Uma vez que o valor de p foi maior que 0,05, nós não rejeitamos o pressuposto de homogeneidade das variâncias.
Sendo assim, podemos proceder para o nosso teste principal, e comparar as médias dos grupos por meio de um teste t de Student. Tal análise indicaria que os grupos diferem significativamente entre si, t(58) = 2,19, p = 0,03.
Em seguida, passamos para os dados da Figura 2, que representam variâncias relativamente heterogêneas entre os grupos. O teste de Levene corretamente acusa esse padrão, F(1, 58) = 32,70, p < 0,001. Como o valor de p foi menor que 0,05, nós rejeitamos o pressuposto de homogeneidade das variâncias. Sendo assim, nós assumimos que os dados são heterocedásticos.
Para prosseguirmos com nossas análises, poderíamos optar por conduzir um teste não paramétrico (como o teste de Mann-Whitney) ou, ainda, realizar o teste t de Welch, que não assume que as variâncias dos grupos são iguais.
Saiba mais: O que é o teste U de Mann-Whitney?

Qual é o código para realizar o teste de Levene no R?
Atualmente, o teste de Levene é facilmente implementado em softwares estatísticos como o SPSS ou o R. No SPSS, o teste de Levene é fornecido na primeira coluna da tabela de saída do teste t para amostras independentes.
Já no R, podemos utilizar a função leveneTest() do pacote car. A seguir apresentamos um trecho de um código mostrando como realizar o teste de Levene no R.
Suponha que você tenha um dataframe de nome dados, com uma coluna denominada grupo (que se divide em A e B, tal como o exemplo de nossa Figura 1), e outra coluna, denominada vd (indicando os escores na variável dependente). A fim de realizar o teste de Levene no R, você pode seguir os passos apresentados no código a seguir:
# carrega o pacote contendo o teste de Levene
library(car)
# executa o teste de Levene
car::leveneTest(dados$vd ~ dados$grupo, # VD ~ VI
center = "median") # computa o centro de cada grupo pela mediana
A saída do teste incluirá a estatística F do teste de Levene, os graus de liberdade do numerador (número de grupos menos 1) e do denominador (número de casos menos número de grupos) e o valor de p associado à estatística F. Em nosso exemplo, os resultados são apresentados a seguir:
Levene's Test for Homogeneity of Variance (center = "median")
Df F value Pr(>F)
group 1 0.0412 0.8398
58
O que corresponde aos valores descritos na seção anterior.
Conclusão
Neste post, você aprendeu o básico do teste de Levene. Esperamos que o post tenha sido útil!
Gostou desse conteúdo? Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Como citar este post
Lima, M. (2023, 18 de janeiro). Teste de Levene. Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/teste-de-levene/













