Neste post, falaremos sobre o teste de postos sinalizados de Wilcoxon. Primeiramente, diferenciaremos a nomenclatura usada na área para os testes de Wilcoxon. Em seguida, explicaremos o conceito de postos, que está subjacente ao cálculo da estatística do teste. Nós então apresentaremos um exemplo, que descreve brevemente o objetivo e as hipóteses do teste de Wilcoxon. Por fim, nós forneceremos um modelo de como reportar os resultados desse teste estatístico.
Teste da soma dos postos de Wilcoxon vs. teste de postos sinalizados de Wilcoxon
Em 1945, o químico e estatístico Frank Wilcoxon apresentou dois testes estatísticos (Wilcoxon, 1945). No artigo original, Wilcoxon descreveu os testes como métodos de ranqueamento (ranking methods), mas que, posteriormente, ficaram conhecido por seu sobrenome.
O primeiro deles é o teste da soma dos postos de Wilcoxon (Wilcoxon rank-sum test), também conhecido como teste de Wilcoxon para duas amostras, teste de Wilcoxon–Mann–Whitney e teste U de Mann–Whitney. Esse teste compara os postos de dois grupos independentes, sendo o equivalente não paramétrico do teste t para amostras independentes.
Por exemplo, se comparamos os níveis de ansiedade de crianças filhas de pais casados versus crianças filhas de pais divorciados, podemos usar o teste da soma dos postos de Wilcoxon.
O segundo teste, que será o foco do restante deste post, é o teste dos postos sinalizados de Wilcoxon (Wilcoxon signed-rank test), também conhecido como teste de postos com sinais, teste de Wilcoxon para pares combinados e teste de Wilcoxon pareado. Esse teste compara os postos de dois grupos dependentes (pareados), sendo o equivalente não paramétrico do teste t para amostras dependentes.
Por exemplo, visando comparar o desempenho de um grupo de adultos em uma tarefa psicomotora após o consumo de água ou de vodca, podemos usar o teste de postos sinalizados de Wilcoxon.

O que são postos?
Postos consistem em uma forma de transformação da variável original. Para explicar o que são postos, daremos um exemplo bem simples. Suponha que observamos os seguintes escores:

Podemos reordená-los em sequência crescente:
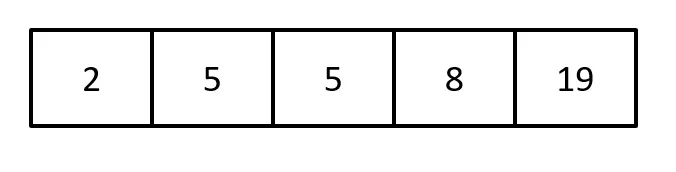
Em seguida, realizaremos a transformação dos escores em postos, por meio da seguinte regra: ao menor escore, atribuíremos o valor 1; ao segundo menor escore, atribuíremos o valor 2; e assim sucessivamente. Caso existam escores iguais, atribuíremos a cada um deles a média dos postos:
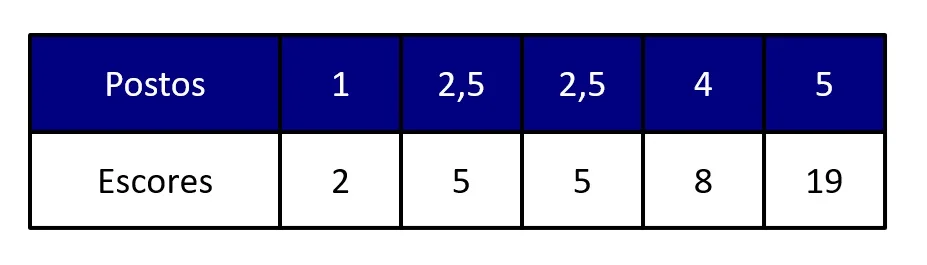
Por exemplo, os postos 2 e 3 estariam associados aos dois escores iguais a 5. No entanto, como não há como determinar a qual escore 5 atribuir o posto 2, e a qual atribuir o posto 3, nós tiramos a média desses postos, (2 + 3) / 2 = 2,5, e atribuímos essa média a todos os postos empatados.
Com base na transformação em postos, agora nossos escores são descritos em nível ordinal: os postos representam a posição relativa do escore, do menor até o maior. Note que os postos comprimem distâncias: os escores 8 e 19, que eram bem mais distantes que quaisquer outros pares de escores adjacentes, agora possuem diferença de apenas uma unidade.
Como os postos comprimem as distâncias entre pares adjacentes de escores, os testes não paramétricos, que se baseiam em postos, são úteis para situações em que a distribuição dos dados é assimétrica (violação do pressuposto de normalidade) ou quando há outliers na amostra.
Além disso, tais testes são úteis quando temos amostras pequenas, inclusive sendo capazes de identificar diferenças que, em certas ocasiões, os correspondentes paramétricos não detectam.
Como veremos a seguir, enquanto o teste t para amostras dependentes analisa as diferenças entre as medidas pareadas, o teste de postos sinalizados de Wilcoxon faz uma transformação dessas diferenças, realizando as análises sobre os postos das diferenças.
O teste de postos sinalizados de Wilcoxon
Exemplo
Vamos entender a lógica do teste por meio de um exemplo. Suponha que selecionamos 10 jovens adultos, que realizaram a mesma tarefa em duas ocasiões distintas, separadas por um intervalo de 1 semana.
Metade dos participantes ingeriu uma dose de água na Sessão 1 e, em seguida, realizou uma tarefa psicomotora. Na Sessão 2, esses participantes ingeriram uma dose de vodca, para depois realizarem a mesma tarefa psicomotora. A outra metade dos participantes ingeriu as bebidas na ordem inversa (i.e., dose de vodca na Sessão 1 e dose de água na Sessão 2).
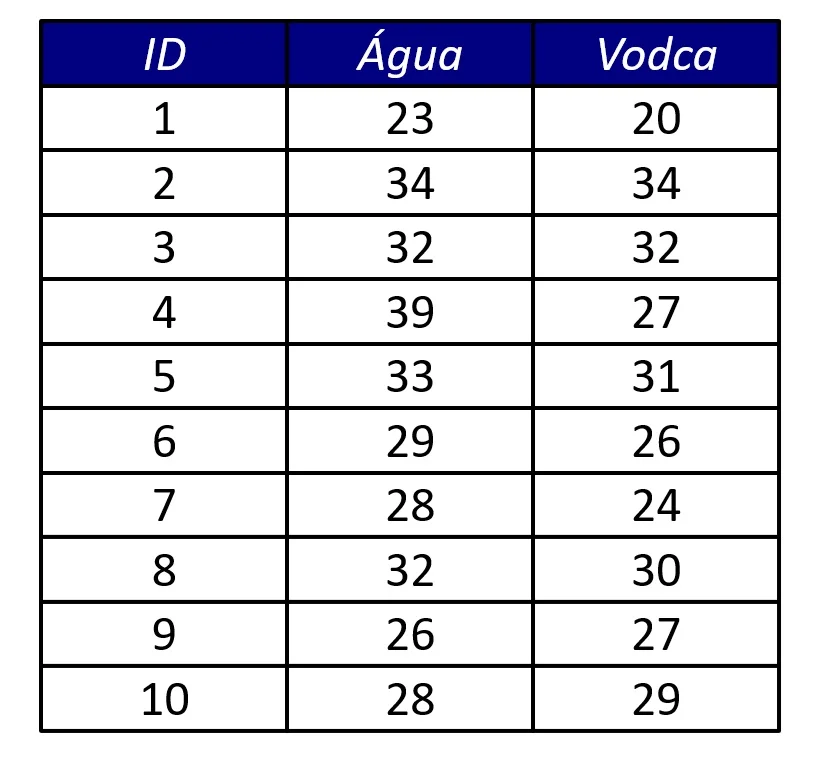
A Figura 1 apresenta os dados desse estudo hipotético. Cada linha da tabela representa um participante, que forneceu dois escores de desempenho. As colunas Água e Vodca contêm o número de acertos, de um total de 60 tentativas, da tarefa psicomotora, para as duas condições experimentais.
Qual é a lógica do teste de postos sinalizados de Wilcoxon?
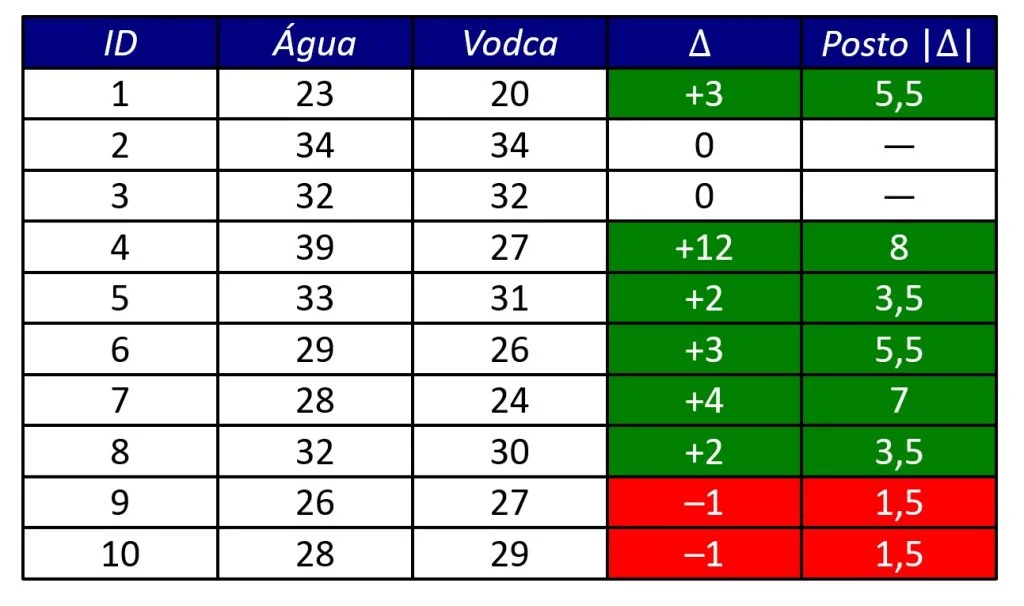
A Figura 2 acrescenta duas colunas ao banco de dados. A coluna Δ (letra grega delta) contém a diferença entre as condições experimentais. Por exemplo, o Participante 1 obteve 23 acertos após ingerir água, e 20 após ingerir vodca. Logo, Δ = 23 – 20 = + 3. O teste t de medidas repetidas cria essa coluna durante seus cálculos.
Já o teste de postos sinalizados de Wilcoxon considera a transformação de Δ. Mais especificamente, esse teste:
- Descarta os escores de diferença iguais a 0 (células brancas na coluna Δ);
- Calcula os postos das diferenças em módulo, isto é, considerando valores absolutos (coluna Postos |Δ|). Por exemplo, os Participantes 9 e 10, tiveram a menor diferença entre condições (Δ = –1). Como eles empataram, ambos recebem o posto (1 + 2) / 2 = 1,5;
- Soma os postos com Δ com sinais positivos (células verdes da coluna Postos |Δ|) e, separadamente, faz o mesmo para os postos com Δ com sinais negativos (células vermelhas da coluna Postos |Δ|).
No SPSS, a estatística do teste é a soma dos postos positivos, representada por T+. No entanto, a depender de como inserimos as variáveis no momento da análise (e.g., Água – Vodca ou Vodca – Água), os postos positivos e negativos se invertem. Sendo assim, você não precisa se preocupar com esses detalhes do algoritmo.
O que você precisa saber é que os softwares transformam a estatística do teste em um escore z (aos interessados nos cálculos, recomendamos Field, 2017, Capítulo 7). Esse escore z representa o quão discrepante a estatística do teste é do valor esperado sob a hipótese nula. O valor de p a ele associado indica quão prováveis são os dados, ou dados mais extremos, considerando a hipótese nula verdadeira.
Quais são as hipóteses nula e alternativa do teste de postos sinalizados de Wilcoxon?
Em seguida, representaremos os escores observados nas medidas repetidas pelo par ordenado (Xi, Yi). Por exemplo, nosso Participante 1 teve 23 acertos após ingerir água e 20 acertos após ingerir vodca, de modo que ele seria representado pelo par ordenado (23, 20).
Em síntese, seguindo a notação introduzida, as hipóteses nula e alternativa do teste de postos sinalizados de Wilcoxon são as seguintes:
- Hipótese nula (H0): as diferenças das observações, isto é, Xi – Yi, são simétricas ao redor de 0;
- Hipótese alternativa (H1): as diferenças das observações, isto é, Xi – Yi, são simétricas ao redor de um valor diferente de 0.
Assim como em outros testes estatísticos, nós definimos um nível de significância (α) e realizamos nossa análise estatística. No caso do teste de postos sinalizados de Wilcoxon, obteremos uma estatística T, um escore z e um valor de p a ele associado. Se p < α, rejeitamos a hipótese nula de que as diferenças pareadas são simétricas ao redor de zero. Em outras palavras, assumimos que os desempenhos na tarefa psicomotora diferiram entre as condições água e vodca.
O teste de postos sinalizados de Wilcoxon compara medianas?
Uma concepção amplamente difundida, porém errônea, é que o teste t compara médias (o que está correto), enquanto o teste de Wilcoxon compara medianas (essa é a parte da concepção que está incorreta). Todavia, uma consulta cuidadosa a Wilcoxon (1945) indica que a palavra median (mediana, em inglês) sequer aparece no artigo.
Vale ressaltar, contudo, que há autores que sugerem o uso da mediana como estatística descritiva dos dados usados no teste de Wilcoxon. Por exemplo, Scheff (2016) recomenda reportar medianas e amplitudes (i.e., valores mínimos e máximos em cada medida pareada), ao invés de médias e desvios-padrões. No entanto, isso não implica que o teste de Wilcoxon esteja comparando as medianas.
Como reportar os resultados de um teste de postos sinalizados de Wilcoxon?
A Figura 3 mostra a saída do SPSS de um teste de Wilcoxon, com base nos dados anteriormente descritos. Se você quer saber como realizar essa análise, então veja nosso post sobre o tema.
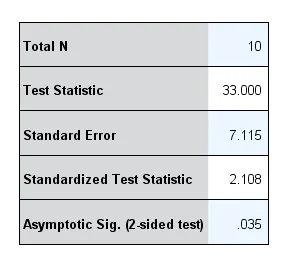
Nos resultados, podemos reportar medianas e amplitudes, conforme sugerido por Scheff (2016). Além disso, é relevante reportarmos o tamanho amostral (Total N), o escore z (Standardized Test Statistic), o valor de p (Asymptotic Sig. (2-sided test)). Adicionalmente, Scheff (2016) sugere que se indique o número de empates, enquanto Field (2017) recomenda acrescentar uma medida de tamanho de efeito nos resultados.
Em nosso exemplo, a medida de tamanho de efeito será o r, que foi igual a 0,53. Para entender como esse valor foi obtido, veja nosso post sobre o tema.
Desse modo, os resultados descritos a seguir servem como sugestão de redação:
O desempenho dos participantes na tarefa psicomotora na condição água (Mdn = 30,5, amplitude = 23–39) foi maior que na condição vodca (Mdn = 28, amplitude = 20–34). O teste de postos sinalizados de Wilcoxon indicou diferenças significativas entre condições, z = 2,11, p = 0,035, r = 0,53. Dois de 10 participantes tiveram desempenhos similares nas duas condições.
Por fim, é digno notar que um teste t para amostras dependentes, conduzido nesses mesmos dados, indicou que as diferenças entre médias pareadas não atingiram os níveis convencionais de significância estatística, t(9) = –1,99, p = 0,077. Isso corrobora o que foi dito anteriormente, de que, em certas circunstâncias, os testes não paramétricos conseguem detectar diferenças que seus equivalentes paramétricos falham em detectar.
Conclusão
Neste post, você aprendeu mais sobre o teste de postos sinalizados de Wilcoxon, o equivalente não paramétrico do teste t para amostras dependentes. Gostou desse conteúdo? Então aproveite e se inscreva em nosso canal do YouTube para ficar por dentro de nossas novidades!
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Scheff, S. W. (2016). Nonparametric statistics. In S. W. Scheff (Ed.), Fundamental statistical principles for the neurobiologist : A survival guide (pp. 157–182). Elsevier. https://doi.org/10.1016/B978-0-12-804753-8.00008-7
Wilcoxon, F. (1945). Individual comparisons by ranking methods. Biometrics, 1, 80–83.
Como citar este post
Lima, M. (2024, 4 de dezembro). O que é teste de Wilcoxon? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/teste-de-wilcoxon/













