Você conhece o teste exato de Fisher? Neste post, explicaremos o que é esse teste, para que ele serve e como calculá-lo, interpretá-lo e reportá-lo. Além disso, por meio de um exemplo simples, forneceremos uma intuição de sua fórmula e do significado do valor exato de probabilidade por ele produzido. Então, sem mais delongas, vamos começar!
Teste exato de Fisher: o que é e quando usar?
Criado pelo estatístico Sir Ronald Fisher, em 1920, o teste exato é uma ferramenta estatística importante em estudos que investigam a associação entre variáveis categóricas.
Por exemplo, as questões a seguir poderiam ser respondidas por meio do teste exato de Fisher: (a) no marketing: existe associação entre o grau de escolaridade e a preferência por determinadas marcas de produtos? (b) na medicina: há associação entre a exposição a um fator de risco (e.g., administração intramuscular de vitamina K) e a presença de uma determinada doença (e.g., leucemia)?
O teste exato de Fisher é uma alternativa ao teste qui-quadrado de independência quando existem células na tabela de contingência com frequências esperadas muito baixas (i.e., menores que 5). Em tais situações, o teste exato de Fisher seria uma opção mais apropriada. Vale ressaltar que o teste exato não depende de qualquer suposição estatística sobre a distribuição dos dados.

Qual é a lógica do teste exato de Fisher?
Anteriormente, descrevemos o que é e quando usar o teste exato de Fisher. O objetivo desta seção, por sua vez, é apresentar uma intuição do que o teste exato de Fisher calcula. Sendo assim, introduziremos um exemplo hipotético a seguir, que será usado ao longo do post.
O que é uma tabela de contingência?
Na pesquisa hipotética descrita neste post, considere que recrutamos 14 participantes. Para cada um deles, perguntamos qual bebida ele prefere (chá, café) e se ele tem insônia (sim, não). O objetivo do estudo foi investigar a associação entre essas duas variáveis. A Figura 1 apresenta os dados da pesquisa.
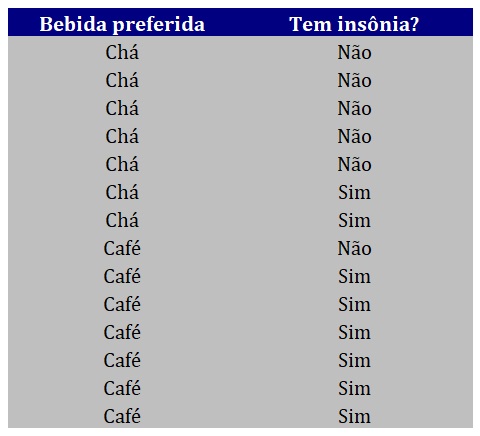
Assim como ocorre no teste qui-quadrado de independência, o teste exato envolve a criação de uma tabela de contingência dos dados observados. Uma tabela de contingência consiste na representação do cruzamento dos níveis de cada variável categórica de interesse. Por exemplo, a Figura 2 apresenta uma tabela de contingências 2 × 2, inicialmente sem valores numéricos.
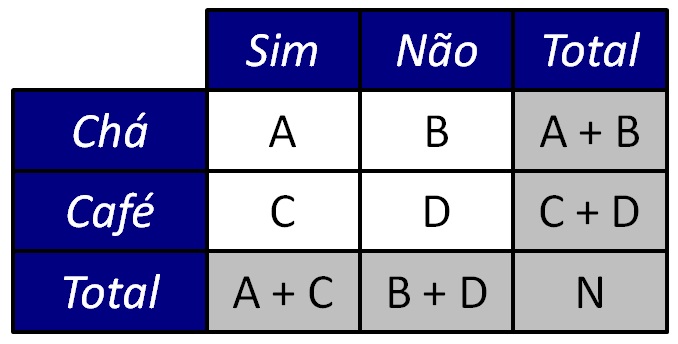
Na Figura 2, as células brancas representam o número de observações para cada cruzamento de níveis das variáveis. Por exemplo, o valor inserido na célula A indicará o número de pessoas que preferem chá e têm insônia, enquanto o valor inserido na célula D indicará o número de pessoas que preferem café e que não têm insônia.
As células cinzas representam os totais marginais, isto é, esses valores correspondem ao somatório dos valores das linhas (A + B e C + D), das colunas (A + C e B + D), ou de todas as células (N).
A Figura 3 apresenta uma nova tabela de contingências 2 × 2, agora preenchida com os valores numéricos da Figura 1. Você pode verificar que os valores das células cinzas representam os totais de linhas, de colunas e geral.
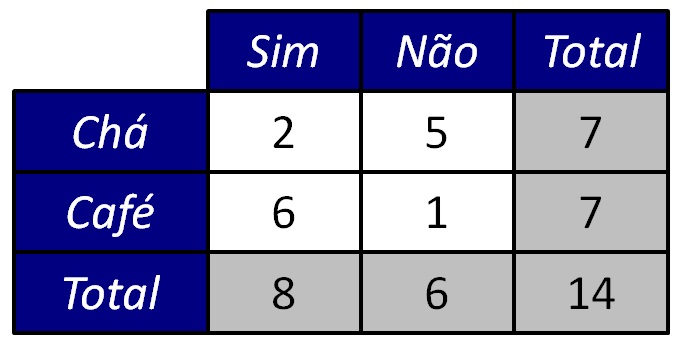
Como pode ser visto na Figura 3, quem prefere café tem uma tendência maior a reportar insônia, comparado a quem prefere chá. Mas essa tendência numérica se traduz em uma associação estatística? Para responder a essa questão, precisamos conduzir um teste inferencial.
O que o teste exato de Fisher faz?
O teste exato de Fisher é um teste condicional, isto é, ele considera todas as maneiras distintas pelas quais as observações (células brancas) poderiam ter ocorrido, com a restrição de que os totais marginais (células cinzas) se mantenham fixos.
Por exemplo, vamos assumir momentaneamente que tivemos apenas 1 participante que prefere chá e que reportou ter insônia em nosso estudo. Mantendo os totais marginais fixos, isso levaria à tabela representada na Figura 4.
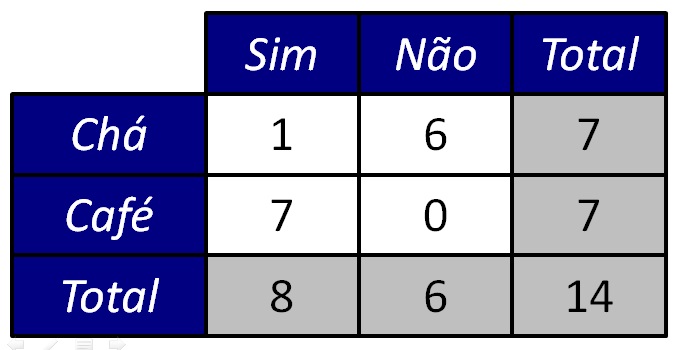
O teste exato de Fisher calcula as probabilidade de ocorrência de todas as tabelas de contingências 2 × 2 possíveis, desde que os totais marginais sejam semelhantes aos dos dados empíricos (Figura 3). O valor obtido expressa a probabilidade exata de se observar uma dada tabela, considerando que a hipótese nula seja verdadeira.
Mas qual é a hipótese nula? A hipótese nula do teste exato de Fisher é de que as variáveis são independentes entre si. Em outras palavras, a independência corresponde a assumir que não existe associação entre bebida preferida e insônia. Se as duas variáveis forem genuinamente independentes, então saber o que uma pessoa bebe não é informativo dela ter ou não insônia (e vice-versa).
Reflita: se não houver associação entre bebida preferida e insônia, qual seria a tabela de contingências mais provável de acontecer? A Figura 5 representa essa tabela.
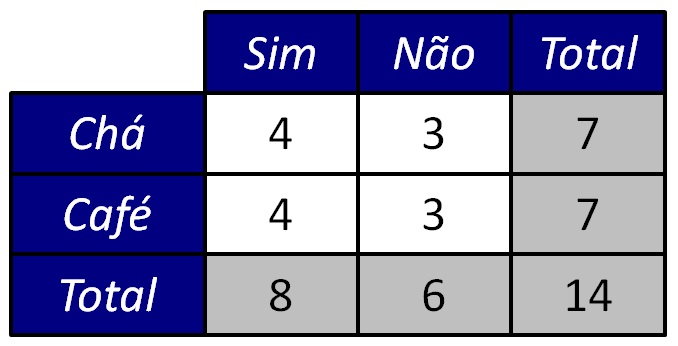
Na Figura 5, o mesmo percentual de participantes que prefere cada uma das bebidas apresenta sintomas de insônia. Se não existir associação entre bebida preferida e insônia, é exatamente esse o padrão que mais esperaríamos observar.
Resumo conceitual do teste exato de Fisher
Em resumo, o teste exato de Fisher:
- Mapeia todas as tabelas de contingências que poderiam ser observadas com base nos totais marginais da tabela empírica;
- Para cada uma delas, calcula a probabilidade de ocorrência daquele cenário;
- Calcula a probabilidade de se observar valores iguais ou mais extremos que o da nossa tabela empírica, considerando-se a hipótese nula verdadeira.
Em seguida, ilustraremos como isso é feito em nosso exemplo hipotético.
Como calcular o teste exato de Fisher?
Como calcular a probabilidade de uma tabela de contingências?
Diversos softwares estatísticos (e.g., SPSS, JASP e R) realizam o teste exato de Fisher de maneira simples e rápida, ou seja, você provavelmente jamais precisará calculá-lo manualmente. No entanto, do ponto de vista didático, é útil entendermos a intuição por trás da fórmula. Desse modo, nosso objetivo aqui é ajudá-lo a compreender o significado do valor de probabilidade gerado pelo teste.
A probabilidade de observarmos uma dada configuração da tabela de contingências, segundo o teste exato de Fisher, é dada pela seguinte fórmula:

onde o ponto de exclamação representa o operador fatorial, isto é, N! = N × (N – 1) × … × 2 × 1.
Embora a fórmula anterior pareça intimidadora, seu significado é simples e elegante: ela gera um valor de p que representa a probabilidade exata de observarmos uma dada configuração da tabela de contingências, condicional aos totais marginais fixos. Assim, quanto menor é o valor de p obtido, mais improvável é que uma configuração seja observada.
Vamos aplicar a fórmula aos dados apresentados na Figura 5, isto é, à tabela que afirmamos ser a mais provável sob a hipótese nula. Aplicando a fórmula, temos:
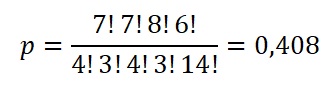
Interpretação: se selecionássemos aleatoriamente 14 participantes que preferem chá ou café, e que têm ou não insônia, uma vez que os totais marginais se mantenham fixos, em 40,8% das vezes observaríamos uma tabela de contingências igual àquela da Figura 5.
Como calcular as probabilidades de todas as tabelas de contingências?
Contudo, precisamos repetir o cálculo anterior para todas as tabelas de contingências possíveis. Por exemplo, dados os totais marginais, existem sete diferentes tabelas de contingências possíveis que poderíamos ter observado. A Figura 6 apresenta essas tabelas, com os valores de probabilidade abaixo de cada uma delas, computados pela fórmula do teste exato de Fisher.

Na Figura 6, a tabela verde sinalizada com um asterisco representa nossos dados (Figura 3). Sendo assim, a probabilidade de observarmos os nossos dados, condicional aos totais marginais fixos, é de p = 0,049.
Interpretação: se selecionássemos aleatoriamente 14 participantes que preferem chá ou café, e que têm ou não insônia, uma vez que os totais marginais se mantenham fixos, em apenas 4,9% das ocasiões observaríamos uma tabela de contingência igual a que obtivemos em nossos dados.
Testes unicaudais ou teste bicaudal?
O valor 0,049 se refere à probabilidade de observarmos valores iguais aos nossos dados, enquanto o teste exato de Fisher visa fornecer a probabilidade de observarmos valores iguais ou mais extremos que os observados em nossa amostra.
Nesse contexto, algo “extremo” é algo improvável, isto é, valores mais extremos são aqueles cujos eventos são menos prováveis que aqueles que observamos. No entanto, o que será considerado “mais extremo” dependerá da hipótese sob consideração. Primeiramente, consideraremos dois testes unicaudais (na mesma direção e na direção oposta ao que observamos). Em seguida, consideraremos um teste bicaudal.
Quando consideramos valores iguais ou mais extremos na mesma direção que o valor que observamos, as tabelas verdes da Figura 6 são as únicas que nos interessam. Desse modo, a probabilidade de obtermos valores iguais ou mais extremos na mesma direção que o observado é p = 0,002 + 0,049 = 0,051. Portanto, assumindo níveis convencionais de significância estatística (α = 0,05), falharíamos em rejeitar a hipótese nula de independência entre bebida preferida e sintomas de insônia.
Por outro lado, quando consideramos valores iguais ou mais extremos na direção oposta que o valor que observamos, com exceção da primeira tabela, todas as demais nos interessam. Desse modo, a probabilidade de obtermos valores iguais ou mais extremos na direção oposta que o observado é p = 0,002 + 0,049 + 0,245 + 0,408 + 0,245 + 0,049 + 0,001 = 0,99. Nesse cenário, também não rejeitaríamos a hipótese nula.
Por fim, em um teste bicaudal, consideraríamos valores iguais ou mais extremos em ambas as direções. Nessa situação, o valor do teste exato de Fisher seria dado pela soma das probabilidades associadas às tabelas verdes e vermelhas da Figura 6, p = 0,002 + 0,049 + 0,049 + 0,001 = 0,10. Mais uma vez, não rejeitaríamos a hipótese nula de independência entre variáveis.
Resumo gráfico do teste exato de Fisher
Note que, na Figura 6, os valores da célula Chá/Sim vão aumentando da tabela superior esquerda até a tabela inferior direita (de 1 até 7). Para fins didáticos, usaremos essa célula como referência.
A Figura 7 sumariza quais valores de probabilidade são somados em cada um dos três cenários descritos na seção anterior (como dissemos, tomando como referência os valores da célula Chá/Sim, na Figura 6).
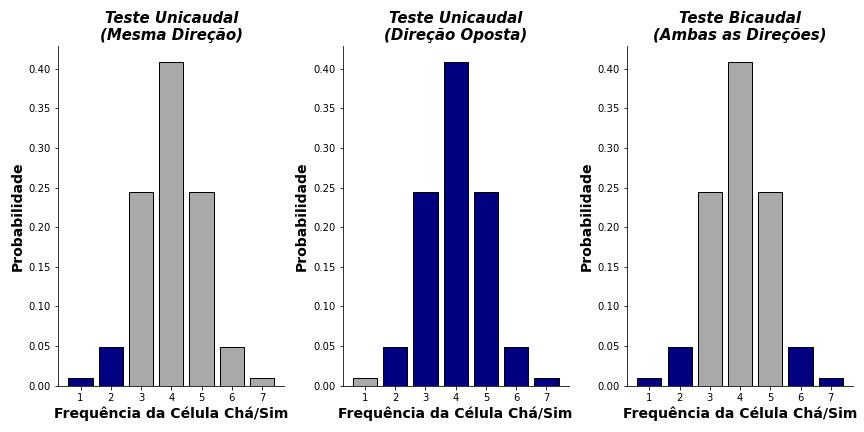
Podemos pensar as distribuições da Figura 7 como um “contínuo”, que vai de uma menor até uma maior tendência de associação entre chá e insônia. Por exemplo, no painel esquerdo, consideramos como valores “mais extremos” apenas tendências baixas da associação entre chá e insônia (em outras palavras, tendências altas da associação entre café e insônia).
Nesse caso, o cálculo de probabilidade considera as probabilidades das tabelas em que a frequência da célula Chá/Sim é 1 ou 2 (indicado no painel esquerdo da Figura 7 pelas barras azuis).
Note que, em todos os painéis, os valores de probabilidades são idênticos. A única diferença entre eles é quais tabelas de contingência são consideradas no cálculo final do valor de probabilidade do teste exato de Fisher (representado pelas barras azuis).
Como executar o teste exato de Fisher no SPSS?
Solicitando a análise
A Figura 8 mostra os dados tabulados no SPSS. Usaremos os mesmos dados descritos anteriormente para executar o teste no SPSS.
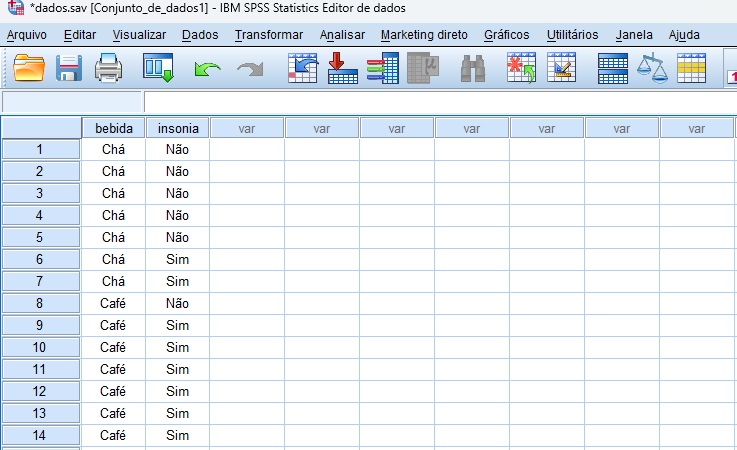
O teste exato de Fisher é solicitado pelo caminho Analisar > Estatísticas descritivas > Tabela de referência cruzada. A Figura 9 ilustra esse caminho.
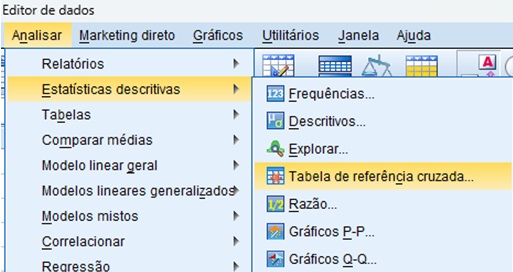
Primeiramente, colocaremos as variáveis de interesse nos menus Linha(s) e Coluna(s). A ordem de especificação das variáveis é irrelevante. Em seguida, clicaremos em Estatísticas, e marcaremos a opção Quiquadrado. Finalmente, clicaremos em Continuar, e depois, em OK. A Figura 10 ilustra essas etapas.
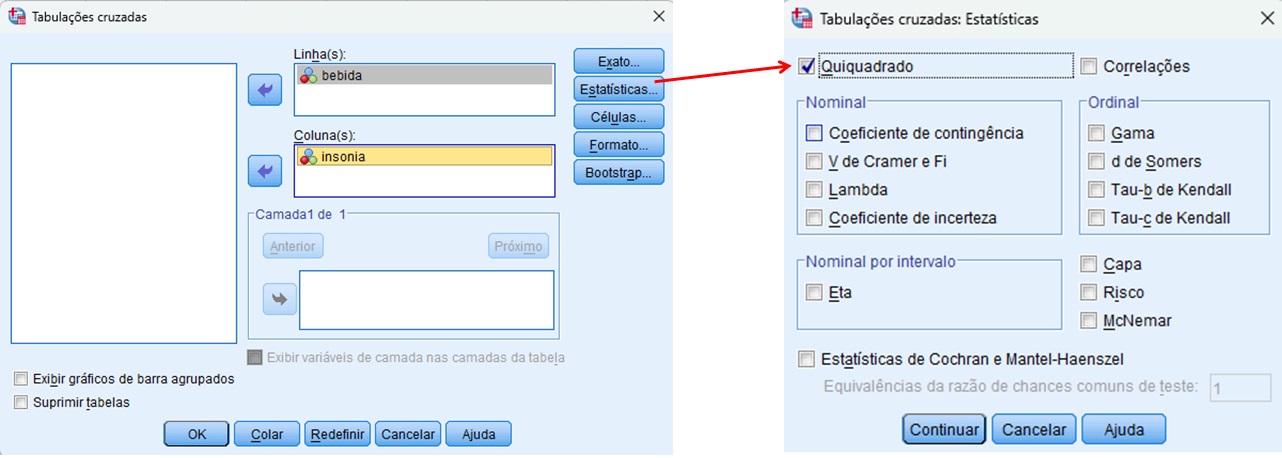
Interpretando e reportando os resultados
A Figura 11 apresenta os resultados gerados pelo SPSS. Primeiramente, vemos uma tabela de contingências 2 × 2 semelhante àquela que apresentamos na Figura 3. Em seguida, na tabela do teste qui-quadrado, a linha na cor azul apresenta as estatísticas do teste exato de Fisher.
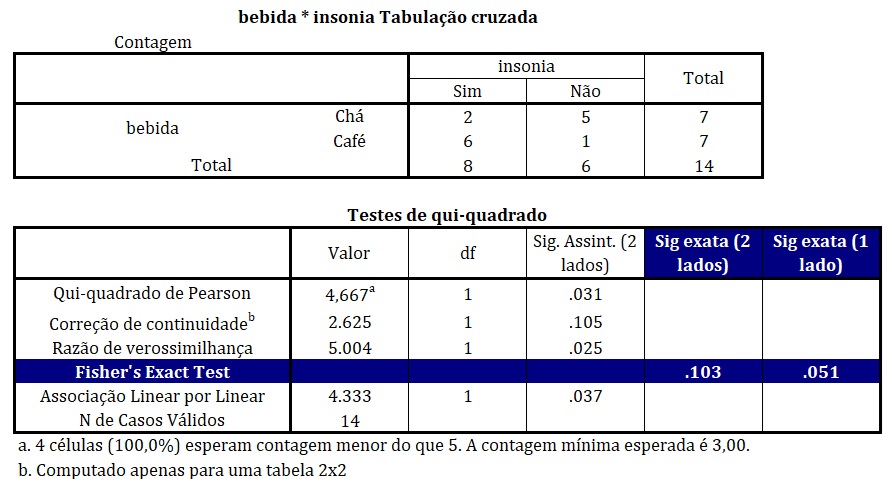
Note, contudo, que o teste exato de Fisher não possui uma “estatística do teste”, a partir da qual se computa um valor de p assintótico. Pelo contrário, como os valores de probabilidade do teste são calculados diretamente a partir dos dados, os valores de p que o teste fornece são exatos (daí o nome teste exato de Fisher).
O SPSS fornece dois valores de p, referentes ao que chamamos de teste unicaudal (mesma direção) e teste bicaudal, na Figura 7. Desse modo, com base em nosso exemplo e em um teste bicaudal, poderíamos fazer o seguinte relato:
A Figura 3 apresenta uma tabela de contingências 2 × 2 cruzando a preferência por bebida (chá, café) e a presença de insônia (sim, não). Embora tenhamos observado uma tendência maior de insônia entre aqueles que preferem café (85,7%), em comparação a aqueles que preferem chá (28,6%), essa tendência não atingiu significância estatística, conforme indicado pelo teste exato de Fisher, p = 0,051.
Conclusão
Neste post, você aprendeu o que é, quando usar e como calcular o teste exato de Fisher. Além disso, por meio de uma análise da fórmula do teste, você teve uma intuição do significado do valor exato de probabilidade gerado pelo teste. Por fim, você viu como solicitar a análise no SPSS, como interpretá-la e como reportá-la.
Aqui, optamos por focar exclusivamente no teste exato de Fisher. No entanto, quando falamos de testes de associação, é comum que os resultados de testes estatísticos sejam acompanhados de medidas de tamanho de efeito, como o coeficiente phi (letra grega φ), o V de Cramer e a razão de chances (odds ratio).
Gostou desse conteúdo? Precisa aprender análise de dados? Então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Howell, D. C. (2013). Categorical data and chi-square. In D. C. Howell, Statistical methods for psychology (8th ed., pp. 137–176). Wadsworth Cengage Learning.
Preacher, K. J., & Briggs, N. E. (2001, maio). Calculation for Fisher’s exact test: An interactive calculation tool for Fisher’s exact probability test for 2 x 2 tables [Computer software]. http://quantpsy.org
Salsburg, D. (2009). Uma senhora toma chá…: Como a estatística revolucionou a ciência no século XX (J. M. Gradel, Trad.). Zahar.
Como citar este post
Lima, M. (2023, 7 de março). Teste exato de Fisher: O que é, quando usar e como calcular? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/teste-exato-de-fisher/













