O teste t de Student é uma ferramenta de estatística inferencial extremamente útil, pois esse teste pode ser utilizado para avaliar se há uma diferença significativa entre as médias de dois grupos em uma característica específica.
Imagine, por exemplo, que uma empresa farmacêutica deseja testar se um novo medicamento contra o câncer aumenta a expectativa de vida dos pacientes. Nesse experimento, formam-se dois grupos: o grupo controle (que recebe um placebo) e o grupo experimental (que recebe o medicamento). O grupo controle apresenta uma expectativa média de vida de 5 anos, enquanto o grupo experimental atinge 6 anos.
Embora o medicamento pareça eficaz, a diferença pode ter ocorrido por acaso. Sendo assim, pesquisadores aplicam o teste t, que, com base em um teste de hipóteses, permite que eles tomem uma decisão de rejeição ou não rejeição da hipótese nula.

Tipos de teste t de Student
Anteriormente, descrevemos o teste t de forma genérica. No entanto, existem três variações principais do teste t, cada uma com aplicações específicas:
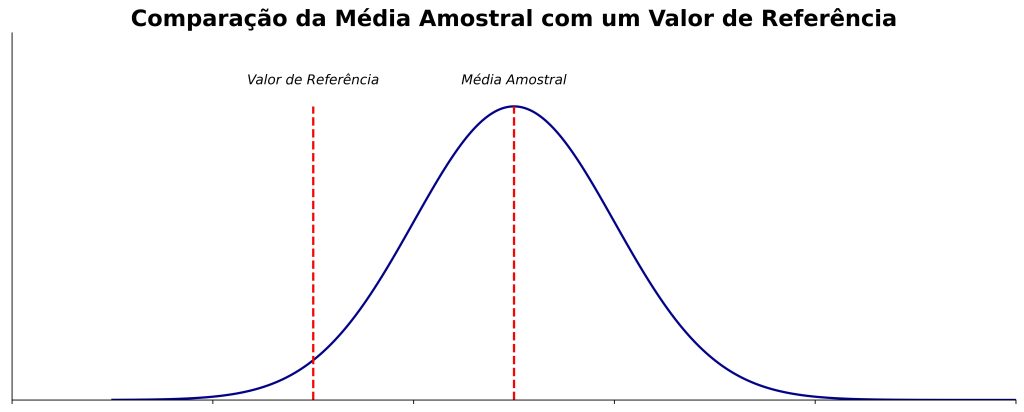
1. Teste t para uma amostra: compara a média de um grupo com um valor de referência conhecido ou pré-definido (Figura 1).
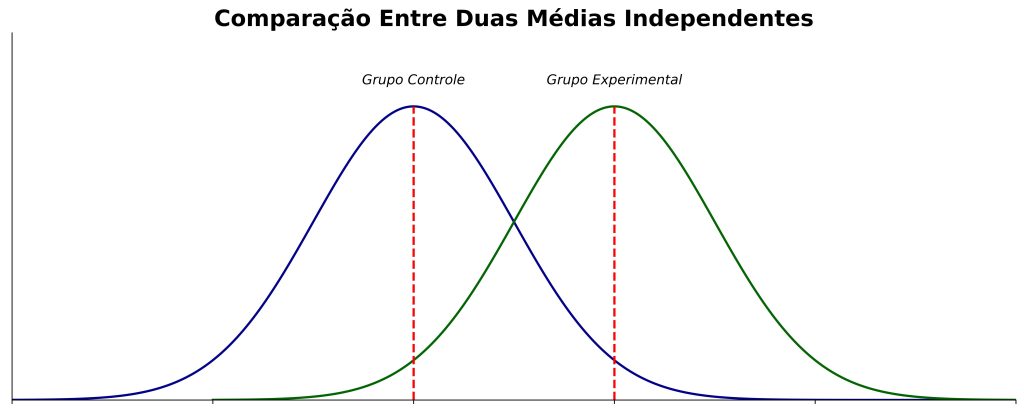
2. Teste t de amostras independentes: compara as médias de dois grupos distintos (Figura 2).
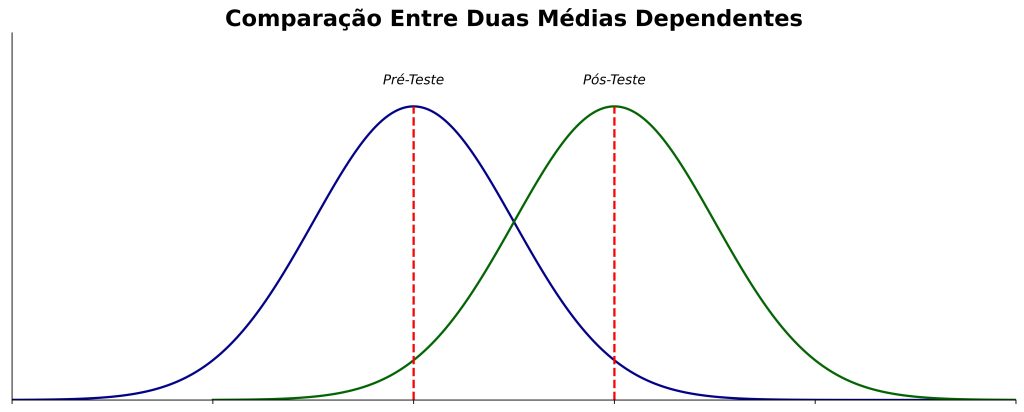
3. Teste t de amostras pareadas ou dependentes: avalia as médias do mesmo grupo em dois momentos diferentes (Figura 3). Por exemplo, podemos comparar um mesmo grupo antes e após um ano de uma intervenção qualquer.
Veja também: Conheça os tipos de teste t
Suposições do teste t de Student
Para utilizar o teste t, é necessário atender a algumas suposições (ou pressupostos estatísticos), já que ele é um teste paramétrico baseado na distribuição normal.
- Normalidade dos dados: no caso dos testes t de amostra única e de grupos independentes, os dados em cada grupo devem vir de populações normalmente distribuídas. Por outro lado, no caso do teste t de amostras dependentes, o pressuposto de normalidade se refere aos escores das diferenças entre as duas mensurações;
- Homogeneidade da variância: no caso do teste t de amostras independentes, as variâncias dos dois grupos precisam ser semelhantes;
- Independência dos escores: para o teste t de amostras independentes, o escore de um participante deve ser estocasticamente independente dos escores dos demais participantes do estudo, isto é, o escore de um participante não prediz o valor do escore de outro participante.
Além disso, o tamanho da amostra desempenha um papel crucial. Amostras maiores tendem a gerar médias mais estáveis e representativas, desse modo aumentando a precisão das estimativas dos parâmetros.
Aplicações práticas do teste t de Student
O teste t é essencial em diversas áreas, como ciências sociais e comportamentais, da saúde e da educação, pois ele facilita comparar dois grupos ou condições em função de uma variável dependente de interesse. Por exemplo, podemos usar os diferentes tipos de testes t para:
- Investigar se o desempenho no Enem de uma determinada amostra difere estatisticamente da nota média do Enem da população em 2023 (teste t para amostra única);
- Comparar o desempenho de alunos expostos a dois distintos métodos de ensino (teste t para grupos independentes);
- Investigar se os níveis de dores de um grupo de idosos diminuiu após eles aderirem e concluírem um programa de exercícios de 4 meses (teste t para grupos dependentes).
Em todos esses casos, o teste t de Student fornece uma maneira confiável de avaliar se as diferenças encontradas têm base estatística sólida.
Conclusão
Gostou deste conteúdo? Aproveite e também se inscreva em nosso canal do YouTube para seguir acompanhando nossas novidades!
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Como citar este post
Lima, M. (2021, 13 de maio). Teste t de Student. Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/teste-t-de-student/













