O teste t para amostras dependentes é um teste estatístico que compara médias dos mesmos indivíduos em duas ocasiões distintas ou sob duas condições diferentes. Neste post, conheceremos um pouco mais sobre esse teste. Primeiramente, introduziremos um exemplo de delineamento de pesquisa que usa o teste t para amostras dependentes. Em seguida, elencaremos as hipóteses nula e alternativa do teste t, e descreveremos conceitualmente a estatística t. Por fim, apresentaremos os pressupostos do teste t.
Exemplo de delineamento de pesquisa
Na tarefa de Stroop, os participantes veem palavras representando nomes de cores. Essas palavras são exibidas em diferentes cores (e.g., palavra AZUL na cor azul). Os participantes devem identificar, rápida e precisamente, a cor da palavra, ignorando o texto. A Figura 1 ilustra tentativas da tarefa.

Nessa tarefa, a variável independente é o tipo de estímulo, que pode ser congruente (e.g., palavra AZUL na cor azul) ou incongruente (e.g., palavra VERDE na cor vermelha), enquanto a variável dependente é o tempo de reação médio (ou mediano) do participante em cada conjunto de tentativas.
Com base na descrição anterior, concluímos que cada participante terá dois escores de tempo de reação, um para cada condição experimental. Esse é um exemplo em que cada participante contribui com escores em duas condições e que, portanto, pode ser analisado por meio de teste t para amostras dependentes.
A Figura 2 mostra um banco de dados típico para esse tipo de análise, com uma coluna de identificação dos participantes (ID), uma coluna indicando os escores em uma condição ou ocasião, e outra com os escores em outra condição ou ocasião. Representamos cada participante em uma linha desse banco de dados.
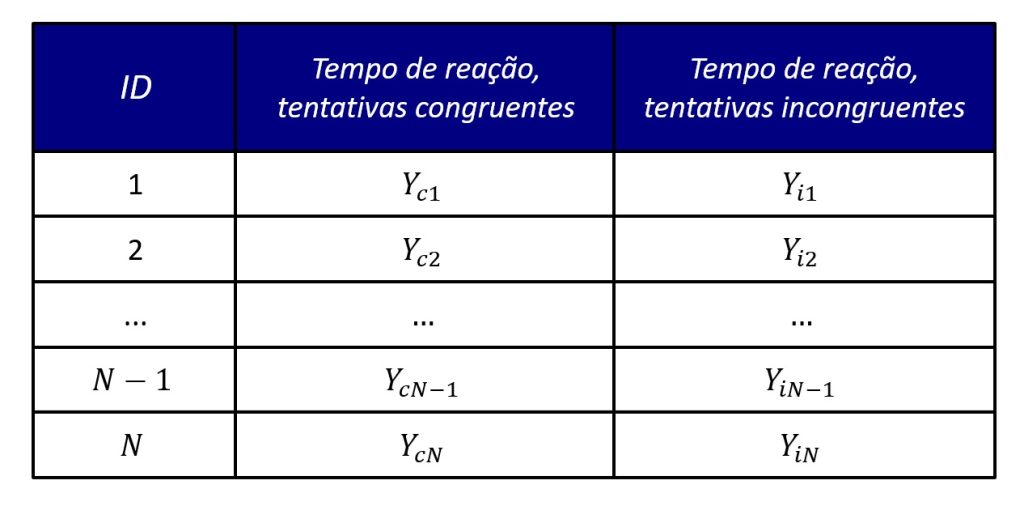
No entanto, existem outras formas pelas quais dados podem ser dependentes, pareados ou emparelhados. Por exemplo, o teste t para amostras dependentes também se aplica para comparar cônjuges, pais e filhos ou, ainda, participantes antes e após uma intervenção experimental.
Em síntese, o teste t é ideal para comparar escores dependentes em variáveis mensuradas nos níveis intervalar ou de razão.
Hipóteses nula e alternativa do teste t para amostras dependentes
Anteriormente, apresentamos a tarefa de Stroop. Nesse exemplo, podemos postular duas hipóteses concorrentes:
- Hipótese nula (H0): μcongruente – μincongruente = 0, isto é, não há diferença entre os tempos de reação médios dos participantes nas condições congruente e incongruente;
- Hipótese alternativa (H1): μcongruente – μincongruente ≠ 0, isto é, há diferença entre os tempos de reação médios dos participantes nas condições congruente e incongruente.
Comumente, definimos a hipótese nula como uma hipótese “zero”, ou seja, uma hipótese de não diferença. No entanto, isso não é estritamente necessário. Além disso, o símbolo ≠ representa um teste bicaudal, que avalia diferenças em ambas as direções. No entanto, poderíamos modificar nossa hipótese alternativa para uma hipótese unicaudal, onde temos a expectativa de que μcongruente – μincongruente < 0. Em outras palavras, essa hipótese unicaudal postula que a incongruência entre cor e palavra irá gerar uma interferência no processamento da informação e, consequentemente, prejudicará os tempos de reação – o chamado efeito Stroop.

Entendendo o teste t para amostras dependentes
Etapas do teste t para amostras dependentes
Conduzimos o teste t para amostras dependentes por meio das seguintes etapas:
- Definir as hipóteses nula e alternativa;
- Estabelecer o nível de significância (α);
- Delinear a pesquisa e coletar dados;
- Calcular a estatística t e o valor de p;
- Decidir se rejeitamos ou não a hipótese nula.
Por exemplo, definimos nossas hipóteses na seção anterior. Em seguida, estabelecemos um nível de significância, α = 0,05. Esse valor indica a probabilidade de cometermos um erro Tipo I, isto é, de erroneamente rejeitarmos uma hipótese nula verdadeira.
Em outras palavras, o α pode ser entendido como o nosso critério do quão surpreendente, ou improvável, os dados precisam ser, para decidirmos “deixar de acreditar” na veracidade da hipótese nula.
Se o valor de p obtido for menor que α, então iremos nos considerar surpreendidos o suficiente para rejeitarmos a hipótese nula. No entanto, se p for maior que nosso α, assumiremos que não temos evidência o suficiente para decidir pela rejeição da hipótese nula.
O que é a estatística t?
Em seguida, coletamos os dados. A Figura 3 apresenta dados de Hedge et al. (2018, Estudo 1, Sessão 1), mas que exemplificam os que poderíamos obter em nosso próprio experimento usando a tarefa de Stroop.
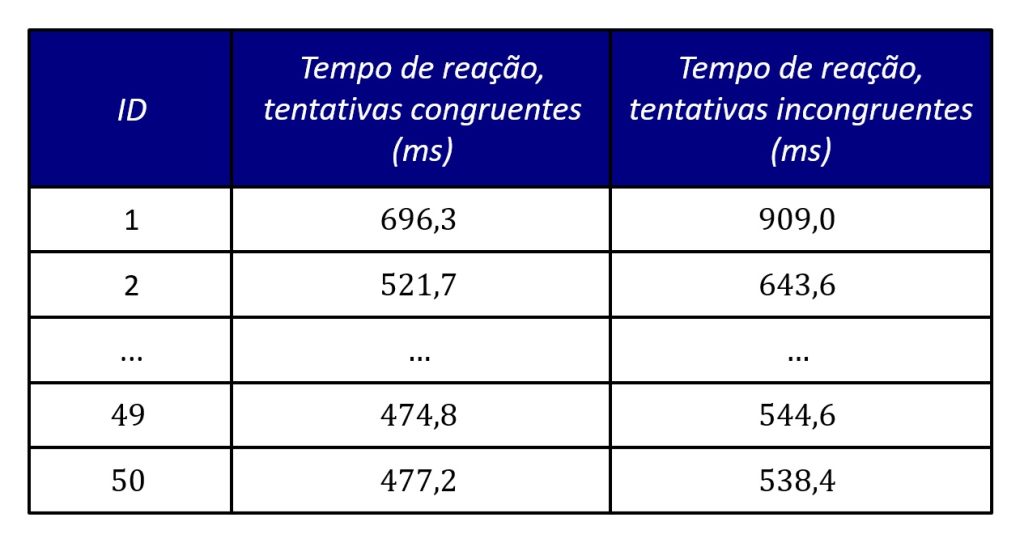
Do ponto de vista descritivo, o tempo de reação foi menor na condição congruente (M = 610,58 ms, DP = 73,49), quando comparada à condição incongruente (M = 688,57 ms, DP = 90,26). A Figura 4 mostra os desempenhos individuais e médios na tarefa.
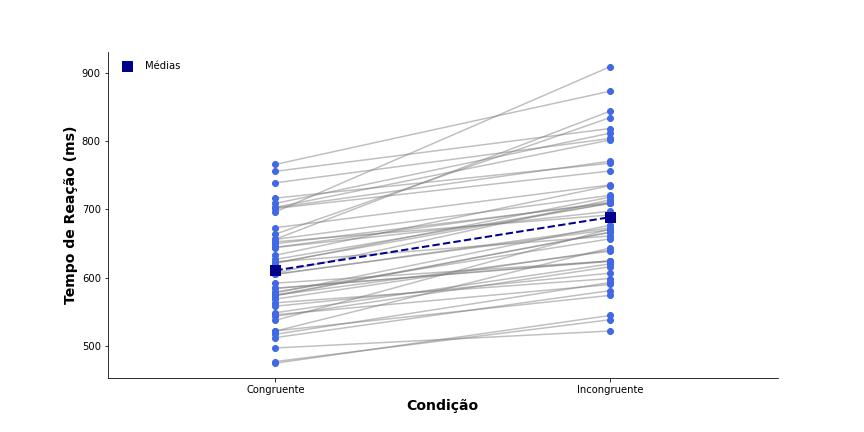
A Figura 4 sugere que houve um custo para a condição incongruente em relação à congruente, cujo valor representa o efeito Stroop (M = 77,99 ms, DP = 38,49). Essas estatísticas correspondem à média e ao desvio-padrão das diferenças entre as condições congruente e incongruente.
Mas essas diferenças descritivas entre as condições se traduzem em diferenças estatísticas? Para respondermos a essa questão, usamos a fórmula do teste t para amostras dependentes:
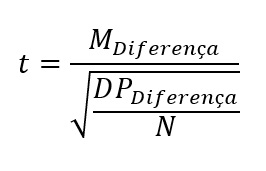
onde N é o número de casos, e a raiz também pode ser definida como o erro padrão da diferença.
Calculando e interpretando o teste t para amostras dependentes
Com base nos valores dos custos da condição incongruente em relação à congruente, temos:
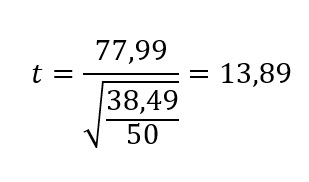
A estatística t, de 13,89, associada a 49 graus de liberdade (gl = 50 observações – 1 = 49), produziu um p < 0,001. Desse modo, como p < α, nós rejeitamos a hipótese nula de que não há diferença entre os tempos de reação médios dos participantes nas condições congruente e incongruente.
Outro modo de compreender o resultado descrito no parágrafo anterior é considerando a distribuição da estatística t com 49 graus de liberdade (Figura 5).
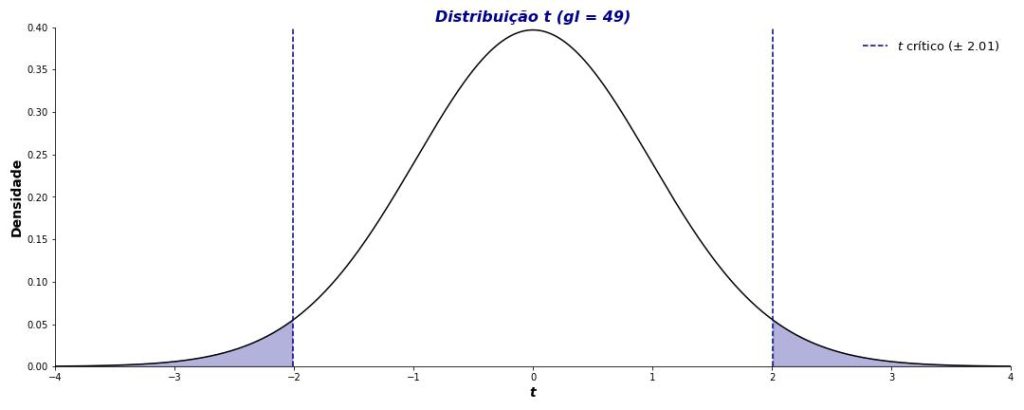
Como podemos ver na Figura 5, a distribuição t é simétrica ao redor de 0, com os valores (em módulo) aumentando nas extremidades das distribuições. Mais importante, as linhas pontilhadas azuis indicam o valor t crítico a um α bicaudal de 0,05.
Essas linhas indicam que 5% dos valores da distribuição correspondem a t > |±2,01|, sendo 2,5% em cada cauda da distribuição. Como tobservado > tcrítico, ele cai na região de rejeição da hipótese nula, sinalizada pela área em azul claro no gráfico. Por isso, assumimos que temos evidência suficiente para rejeitarmos a hipótese nula.
Quais são os pressupostos do teste t para amostras dependentes?
O teste t para amostras dependentes possui os seguintes pressupostos:
- Normalidade: os escores das diferenças entre as duas condições devem seguir uma distribuição normal. Em outras palavras, este teste t não exige que as distribuições das condições sejam normais, mas sim que a distribuição das diferenças entre uma medida e outra seja normal;
- Independência: as observações precisam ser independentes entre si. Por exemplo, quebraríamos esse pré-requisito se duas pessoas realizassem a tarefa simultaneamente, e ficassem conversando uma com a outra durante a tarefa;
- Pareamento dos escores: é possível combinar pares de observações, tais como escores em condições ou ocasiões distintas, escores de diferentes cônjuges, de gêmeos ou de empregador e empregado, para citar alguns exemplos.
Conclusão
Neste post, você aprendeu os fundamentos do teste t para amostras dependentes. Contudo, lembre-se que de que existem outros tipos de teste t, como o teste t para amostras independentes.
Se você precisa aprender análise de dados, então faça parte da Psicometria Online Academy, a maior formação de pesquisadores quantitativos da América Latina. Conheça toda nossa estrutura aqui e nunca mais passe trabalho sozinho(a).
Referências
Field, A. (2017). Discovering statistics using IBM SPSS Statistics (5th ed.). Sage.
Hedge, C., Powell, G., & Sumner, P. (2018). The reliability paradox: Why robust cognitive tasks do not produce reliable individual differences. Behavioral Research Methods, 50, 1166–1186. https://doi.org/10.3758/s13428-017-0935-1
Como citar este post
Lima, M. (2021, 22 de outubro). Teste t para amostras dependentes. Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/teste-t-para-amostras-dependentes/














